はじめに
これはレイトレ合宿アドベント・カレンダー(2017)の記事です。
ライト・トランスポートやサンプリングは賢い人たちの仕事なのでそちらに任せて、ここでは少し趣向を変えて行列を使ってポリゴン・メッシュのデータを扱う方法について解説したいと思います。
ウィングド・エッジといったデータ構造は聞いたことがある人が多いかもしれませんが、一度行列を使った方法を身につければ、メッシュ処理において他のデータ構造は必要なくなると言っても過言ではないでしょう。なぜなら、行列での記述は汎用性が高いですし、いったん疎行列を用意すれば、様々な処理を簡潔に記述できるからです。特に面白いのはメッシュの操作、例えばリダクションなども行列の演算で記述できるようになるということです。この記事では2つのタイプの行列を紹介したいと思います。
一つ目の方法
まず初めに"Trivial Connections on Discrete Surfaces"のMATLABでの実装例で使われていた方法を紹介します。これはメモリ消費量の観点からいうと、無駄がありますが、非常に分かりやすく、便利です。
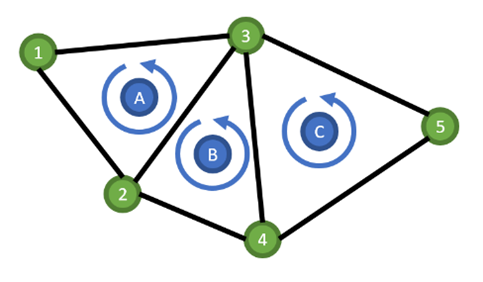
Figure1 シンプルな三角形メッシュ 反時計回りを表とする
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | \ | A | |||
| 2 | \ | A | B | ||
| 3 | A | B | \ | C | |
| 4 | B | \ | C | ||
| 5 | C | \ |
Figure2 上の三角形メッシュを表す行列 行と列はそれぞれ頂点
ここでは、三角形は反時計回りが表であると定義しましょう。まずFigure1の三角形Aの情報を行列に落とし込んでいきます。青い矢印の流れに沿って、2番の頂点から3番の頂点に向かうとき、自身がその辺の左側にあれば、2行3列にAを入れます。同様に、3行1列、1行2列目にも、Aが入ります。今度は逆に、3番の頂点から2番の頂点に向かうとき、三角形Bがその辺の左側にあります。ですので、3行2列にBが入ります。このように行列に三角形のインデックスを登録していくと、Figure2のような疎な行列が出来上がります。
さて、辺が主体となって扱われる、この行列の何が便利なのでしょうか?
一番の利点は、隣あう三角形を簡単に求めることができるところです。三角形のデータ構造は通常、3つの頂点のインデックスを持ち、当たり前ですが、各辺の両端の頂点のインデックスはすぐに分かります。例えば三角形B(3頂点のインデックスは2,3,4)の隣り合う三角形を求めたい場合、3行4列、2行3列、4行2列、の3か所を見ればよいことが分かります。4行2列は空なので、その辺は境界であることが分かります。この表現方法はメッシュ上で塗りつぶしを行う場合や、ベクトル場をたどって、流れを線によって可視化する場合などに役に立ちます。
また、境界があるかどうかを利用すれば、メッシュが閉じているかどうかを調べることができます。閉じていない三角形メッシュに、SSSやガラスのシェーダ (これらはしばしばメッシュが閉じていることを前提に作られています) が割り当てられた場合、事前に警告を出してユーザに知らせることができます。スキャンされたメッシュ・データに穴が空いていて、レンダリング途中でシェーダが予期せぬ入力のためNanなどを出力してしまうことを事前に防ぐことができるのです。開発者がデバッグする際にも役立つでしょう。行列にメッシュの情報を落とし込むときに、すでに値のある所に再度値を書き込むことになれば、入力されたものがノン・マニフォルド・メッシュであることも分かります。
もうお気づきかもしれませんが、ある頂点の価数(いくつの三角形がその頂点に属するか)も簡単に調べることができます。例えば、頂点3に属する三角形は、行列の3行か、3列目どちらかをたどれば分かります。これは、頂点ごとのスムージングされた法線などを計算するときも便利です。
ある頂点に隣接する頂点を探すには、その頂点に属する三角形をリストアップし、リストアップされた三角形の頂点から重複分を除外することで、比較的簡単に求められます。
二つ目の方法
次に、Eurographics2017の論文"A GPU-adapted Structure for Unstructured Grids"で使用されているものを紹介します(導入した最初の文献はこれではないと思います)。使用されているメッシュ行列は以下のような形式の単純なもので、論文中では$M$と表記されます。
| A | B | C | |
|---|---|---|---|
| 1 | 1 | ||
| 2 | 2 | 1 | |
| 3 | 3 | 2 | 1 |
| 4 | 3 | 2 | |
| 5 | 3 |
Figure3 メッシュ行列$M$ 行は頂点で列は三角形 行列の要素はそれぞれの三角形での頂点のならび順
さらに簡便のため、以下のような二値化メッシュ行列を使います。ここでは論文と異なりますがbinaryの頭文字をとって $B$と書くことにしましょう。
| A | B | C | |
|---|---|---|---|
| 1 | 1 | ||
| 2 | 1 | 1 | |
| 3 | 1 | 1 | 1 |
| 4 | 1 | 1 | |
| 5 | 1 |
Figure4 二値化メッシュ行列$B$ 先と同様に行は頂点で列は三角形 先ほどの行列の値が入っているところを単純に1で置き換えたもの
ちなみにメッシュに三角形しか含まれない場合は、$M$の要素は1から3までなので、メモリを節約するためよりコンパクトな表現ができますが、詳細が知りたい方は論文を参照してください。
この論文では、明示的に中間データを生成するコスト(メモリ領域を確保するコストは馬鹿にできません)や、メモリ消費量を抑えるため、アクション・マップという考え方を導入しており、これが論文の核心部分となっています。アイデアは非常に単純ですが、多くのアプリケーションに応用できるものなので、以下ではアクション・マップに焦点を当てましょう。
一番簡単な例としてあげられているのは、三角形の重心を求める処理です。三角形の重心のベクトル$G$は
G=\frac{1}{3} B^T P
として求めることができます。Pは頂点を並べた行列で列が$x$,$y$,$z$に対応します。ここで行列$B$の転置を明示的に求めた場合、$M$と$B$の転置の2つがメモリにストアされることになり、メモリが無駄に消費されてしまいます。アクション・マップを使った方法では、$G=1/3 B^T P$の計算の最中に$B^T$の要素を$M_{ij}$にマップ$Q(M_{ij})$を適用することで求めます。基本的にはたったこれだけのアイデアなので、簡単な処理では無意識に使っている人も多いのではないでしょうか?
表記方法ですが、行列$M$の要素$(1,2,3)$を$(1,1,1)$に置き換えるアクション・マップを適用する場合、
M_{(1,2,3)→(1,1,1)}
と書きます。
次に単純な例は、三角形の法線を求めるものです。三角形の2つのエッジは
P_1 P_2=M^T_{(1,2,3)→(-1,1,0)}P
それから、
P_1 P_3=M^T_{(1,2,3)→(-1,0,1)}P
として求められます。正規化されていない頂点の法線は、
N_v=M_{(1,2,3)→(1,1,1)}N_f
として書くことができ、ここで$N_f$は$P_1$ $P_2$と$P_1$ $P_3$の外積です。すべての計算はアクション・マップをつかって$M$のみを使用して行うことができます。少し複雑な処理になると、中間データを必要としない利点がより明らかになってきます。一つ目の行列の使い方であったような価数は、二値化されたメッシュ行列とその転置の積$S_v=BB^T$をアクション・マップによって計算することで、簡単に求められます。この行列の対角成分$i$行$i$列は頂点$i$に属する三角形の数であり、また非対角成分$i$行$j$列はエッジ$ij$に属する三角形の数になっています。この行列を使うことでもメッシュが閉じているかどうかを判別することができます。
少し話がそれますが、メッシュが複数の独立したパーツからなる場合は、非正規化グラフ・ラプラシアンの固有値0に属する固有ベクトルを求めることによって、ラベリングすることが出来ます。MayaなどDCCツールにはそういった機能が搭載されていますが、動作が遅いことが多いので、自分で作ってみてもよいでしょう。表記はもっとシンプルにできたのではないかとは思いますが、日本語の解説では石黒勝彦氏による「関係データ学習」という書籍が分かりやすいと思います。また、「関係」を可視化する方法は"Visualizing Group Structures in Graphs: a Survey"によくまとまっています。グラフのノードを円グラフにしたものなどは、なかなか思いつかないのではないでしょうか?可視化することによって、形状の認識や識別をするためのアプリケーションを作る際、様々なヒントが得られるかもしれません。
| A | B | C | |
|---|---|---|---|
| A | 3 | 2 | 1 |
| B | 2 | 3 | 2 |
| C | 1 | 2 | 3 |
| Figure5 隣接行列$S_f=B^T B$ |
さて、同様に$S_f=B^T B$を考えてみましょう。対角成分は面の頂点数、非対角成分には共有される頂点の数が入っています。つまり、2つの面がエッジを共有している場合には2が、1つの頂点のみが共有されている場合には1が入ります。この隣接行列を使ってもどの面が境界にあるかを知ることができます。ある行に注目して、非対角成分のうち要素が2であるものの数が対角成分の要素と一致するときは、すべての辺が2つの面によって共有されていることになります。このとき面は他の面に囲まれているため、境界上にありません。
| A | B | C | |
|---|---|---|---|
| A | 1 | ||
| B | 1 | 1 | |
| C | 1 |
Figure6 双対行列$A_d$
$S_f$の要素のうち2である部分だけを1とし、それ以外を0とした行列は双対行列$A_d$と呼ばれます。$A_d$は2つの面によって共有されている辺の部分にのみ1が入っていることからメッシュの双対を表していることが分かり、Figure6の行列はAとB、BとCが隣り合っていることを意味しています。隣り合った面の重心同士をつなぐことで双対が作れます。
最後にトポロジーの変化をともなう場合について少し説明します。面や頂点の削除は行列の操作として実装することができます。例えば、エッジ$ij$を削除したあとのトポロジーは
B^{'}=KB
と表すことができます。ここで$K$は頂点数$x$頂点数の単位行列の$j$行$j$列を0、$i$行$j$列を1としたものです。ただしメッシュ行列を同様の方法で更新した場合、処理で影響を受けた要素のみインデックスを更新する必要があります。
メッシュのリダクションは本来シーケンシャルなものなので、並列化する場合には注意が必要です。この論文では部分ごとの演算を同時に行えばいいと書かれていますが、この並列操作に関してはより良い方法が"Instant Level of Detail"で提案されています。こちらの論文ではQEMと呼ばれるリダクションによるエラーがローカル・ミニマムになる部分を並列に削除することで、メッシュが崩れないよう工夫がしてあります。
最後に
行列を使ってポリゴン・メッシュを扱う方法を紹介しましたが、どうでしょうか。疎行列だけあれば十分な気がしてきませんか?他にも面白い行列の使い方はたくさんあると思うので、こういうテーマで研究をしても面白いと思います。レンダラを作るには、レンダリング以外の論文も大いに役立ちます。