はじめに
matplotlibを用いてベクトル場の可視化を行う。例として高校の物理学で学ぶ静電場および静磁場をプロットする。
どのプログラムも,流れとしては
1. numpyのmeshgridメソッドで描画のためのx,yメッシュを作り,
2. 生成された(x,y)点上でベクトル関数$F(u(x,y),v(x,y))$を定義し
3. 様々なオプションをつけてメッシュ上に矢印(ベクトル)を描画する,
というものである。
具体例を見ながら動作を確認すると分かりやすいだろう。
内容
(1) 1つの点電荷が作る静電場の可視化
(2) 2つの点電荷(電気双極子)が作る静電場
(3) 原点を通る定常電流が作る静磁場
(4) 3次元ベクトル場 (原点においた点電荷が作る静電場)
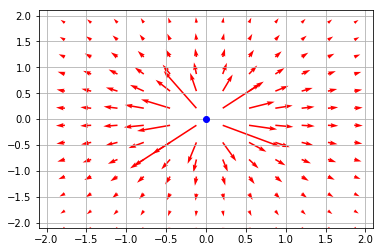
(1) 1つの点電荷が作る静電場の可視化
"""
(1) 原点にある1つの点電荷が作る静電場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=2.1,2.1 # メッシュのためのパラメータ
gridwidth=0.33
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth)) # メッシュ生成
R = np.sqrt(X**2+Y**2) # 原点からの距離
#点電荷の位置座標と電荷
X1,Y1=0,0 # 原点への電荷の配置
Q1=1 # 電荷量の設定
R1=np.sqrt((X-X1)**2+(Y-Y1)**2) # この電荷から任意点(X,Y)までの距離
plt.plot(X1,Y1,'o',color='blue') # 点電荷を描画
# ベクトル関数 F(U(x,y), V(x,y))を定義。静電場の表式を用いる。
U = Q1*(X-X1)/(R1**2)
V = Q1*(Y-Y1)/(R1**2)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=5.0) # ベクトル場をプロット
plt.xlim([-LX,LX]) # 描くXの範囲
plt.ylim([-LY,LY]) # 描くyの範囲
# グラフ描画
plt.grid()
plt.draw()
plt.show()
結果(1)
(2)2つの点電荷(電気双極子)が作る静電場
"""
(2) 2つの点電荷(電気双極子)が作る静電場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=2,2
gridwidth=0.2
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth))
R = np.sqrt(X**2+Y**2)
#2つの点電荷の位置座標と電荷
X1,Y1=1.1,0
Q1=1
R1=np.sqrt((X-X1)**2+(Y-Y1)**2)
plt.plot(X1,Y1,'o',color='blue')
X2,Y2=-1.1,0
Q2=-1
R2=np.sqrt((X-X2)**2+(Y-Y2)**2)
plt.plot(X2,Y2,'o',color='blue')
##
#ベクトル関数の設定。2電荷分。
U = Q1*(X-X1)/(R1**2)+Q2*(X-X2)/(R2**2)
V = Q1*(Y-Y1)/(R1**2)+Q2*(Y-Y2)/(R2**2)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=6.5)
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
plt.draw()
plt.show()
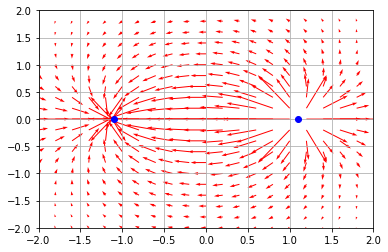
結果(2): 2つの点電荷(電気双極子)が作る静電場
(-1.1,0)と(1.1,0)におかれた二つの点電荷(電荷はそれぞれ1と−1)が作る静電場。
(3) 原点を通る定常電流が作る静磁場
"""
(3) 原点を通る定常電流が作る静磁場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=3,3
gridwidth=0.3
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth))
R = np.sqrt(X**2+Y**2)
#点電荷の位置座標と電荷
X1,Y1=0,0
I=1 #定常電流の値
R1=np.sqrt((X-X1)**2+(Y-Y1)**2)
plt.plot(X1,Y1,'o',color='blue')
#ベクトル関数の設定。定常電流が作る静磁場 F(U(x,y), V(x,y))
U = I*-1*(Y-Y1)/(R1)
V = I*(X-X1)/(R1)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=4.5)
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
plt.draw()
plt.show()
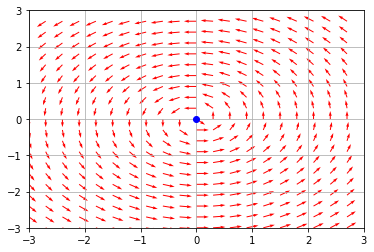
結果(3) 定常電流の作る静磁場
原点から紙面に垂直に続く定常一様電流Iが作る静磁場。
(4)3次元ベクトル場 (原点においた点電荷が作る静電場)
"""
(4) 3次元ベクトル場の図示
原点においた点電荷が作る静電場
"""
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D #3次元プロットのためのimport
import numpy as np
fig = plt.figure()
ax = Axes3D(fig)
LX, LY, LZ = 2,2,2 # xyzメッシュのパラメータ
gridwidth=0.9 #
X, Y, Z= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth),np.arange(-LZ, LZ, gridwidth) ) #メッシュ生成
R = np.sqrt(X**2+Y**2+Z**2)
#点電荷の位置座標と電荷
X1,Y1, Z1=0,0,0
Q1=1
R1=np.sqrt((X-X1)**2+(Y-Y1)**2+(Z-Z1)**2)
ax.scatter3D(X1,Y1,Z1,"o", color='blue')
U = Q1*(X-X1)/(R1**2)
V = Q1*(Y-Y1)/(R1**2)
W= Q1*(Z-Z1)/(R1**2)
ax.quiver(X, Y, Z, U, V, W, color='red',length=1, normalize=False)
ax.set_xlim([-LX, LX])
ax.set_ylim([-LY, LY])
ax.set_zlim([-LZ, LZ])
plt.show()
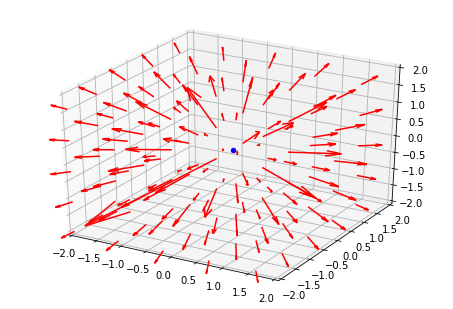
結果(4) 3次元ベクトル場 (原点においた点電荷が作る静電場)
原点に置かれた点電荷が作る電場の3次元プロット。