前提
・ある曲のサビ30秒間を抽出してメル周波数ケプストラム分析をする。
・2曲間のKLダイバージェンスを求める。
・↑視覚化する
・主成分分析したものを視覚化する
・相関行列になっていれば成功
データ
AKB48のフライングゲットとヘビーローテーションを比較する。
求めたKLダイバージェンスは16×16次元
[[ 95.31099625 91.15557772 56.59372546 112.20285226 94.41219084
211.66976101 92.55439072 121.40280516 99.87466514 76.50081387
176.93201868 91.81223113 85.27707457 105.14295556 125.49246929
130.92378707]
[ 61.39054933 94.3470823 62.02704779 107.94425798 128.17543843
309.20131854 90.24173322 107.68055813 109.89023764 50.34427017
223.12270163 86.42437451 56.75452679 147.27774644 140.3949859
183.75894278]
[ 105.66621666 82.44161726 55.37485991 95.92704467 71.93089191
139.99784461 103.5305553 104.49783045 101.97799459 97.42010348
125.64532251 93.76049908 96.99409273 81.04788291 101.66325191
106.66200182]
[ 72.58173889 88.12377418 61.89530358 86.95335195 138.72571321
312.35785101 90.41438615 113.71909706 118.77928154 65.50818774
214.00175004 113.10626452 52.0092669 135.97299857 148.63792688
193.27541302]
[ 81.63626278 89.21027233 65.00120995 130.11972589 98.52470863
225.72264868 91.47807602 108.48086909 82.19549295 60.1953677
178.25090454 74.23288462 86.75234338 119.57743314 121.44196645
130.71085354]
[ 112.80955973 84.20293672 66.13356741 126.27130948 60.46044078
108.98487829 94.30643082 114.27767382 85.12283233 100.1694529
123.12525354 77.02509766 127.07893463 77.72584545 90.34136209
77.31272758]
[ 98.67181854 79.9882436 60.27699343 95.48883179 57.14726547
106.75881027 84.51898243 105.15391427 96.42217442 103.36893403
115.31304902 81.72145888 113.92827284 70.10342339 79.76864038
85.59532391]
[ 124.00540056 102.49330066 69.46940492 117.7972943 65.92281076
122.42686859 109.21028055 139.69386525 120.41384311 124.96030812
147.40336555 98.98037785 136.61224331 82.25578681 101.68799841
101.60176282]
[ 141.02536187 88.11442192 69.53316552 123.67378376 67.97351381
111.42573997 108.78252174 128.35881238 103.34373259 117.07395769
122.29312541 102.2082161 129.57301791 78.33587137 110.68395808
89.29850647]
[ 105.83495569 71.55826188 60.84049422 93.8003492 77.06177205
150.83061505 86.87908254 114.92215578 100.28873519 90.46477627
134.67789323 96.1906124 94.92596407 79.28705749 103.96680059
107.35708818]
[ 166.21174246 116.41752126 94.20800055 148.72009053 61.35802568
82.62043669 132.79504129 158.40382344 130.28234204 168.90800616
131.6410988 114.45081907 191.85294161 84.81226445 106.30195098
89.39215458]
[ 65.41033607 67.36512259 45.30766447 70.95585215 66.52775288
140.37168343 69.72982884 81.57225523 87.82282686 67.15724897
121.30574971 69.68125315 67.9074851 76.44269754 77.95359039
98.47073341]
[ 93.18094019 77.11815575 56.16982799 74.68534181 85.72265797
159.071974 86.2112096 110.31931314 105.62643628 95.54275032
131.41625514 110.34370673 79.29159169 78.66368263 104.24385502
122.82713447]
[ 151.91835442 95.8700754 78.95950183 106.69723914 66.8965109
83.65254447 116.18496042 145.24555922 122.32195846 154.69915632
107.94328396 128.95019683 145.70673878 67.11698712 105.83368936
95.34869169]
[ 77.74571566 68.14642544 49.52404341 90.78773066 80.01443641
181.90010793 78.31102815 87.9577934 82.56031457 62.65435512
139.59025763 74.27213077 71.97330552 91.39001379 99.40086861
112.40496471]
[ 80.29039282 80.71088572 58.43570222 109.4784385 67.87835361
153.32727136 84.13107423 99.60128605 93.34917358 74.31430677
147.10640919 65.51538298 99.68106666 93.5848086 87.98955945
99.60590161]]
視覚化
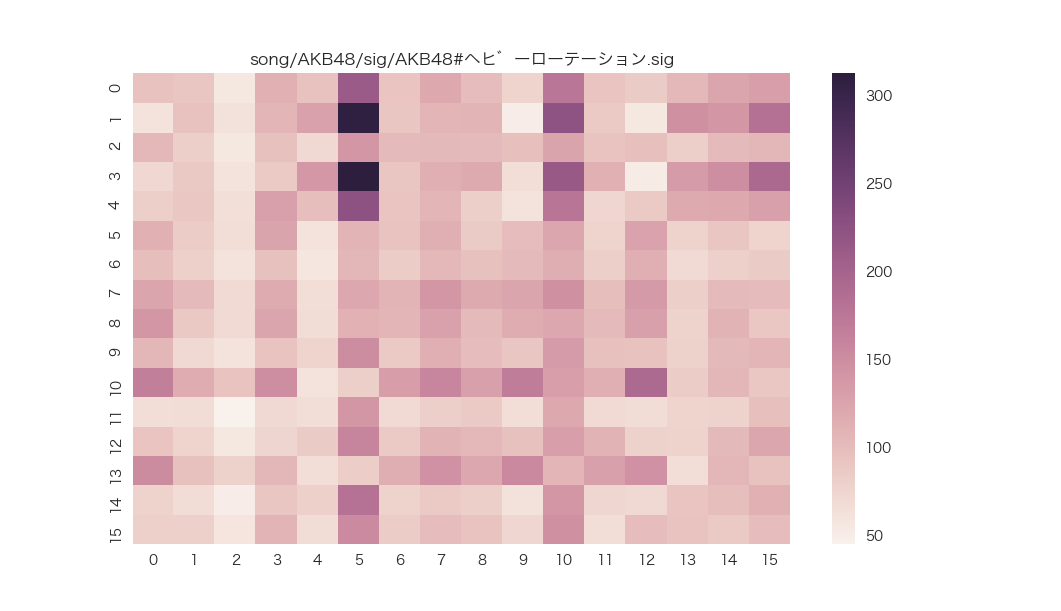
ヒートマップで描画する。
グラフをきれいに表示できるseabornというライブラリを使う。
※タイトルが文字化けしたので日本語化する必要がある
site-packages/seaborn/rcmod.pyを編集
def set(context="notebook", style="darkgrid", palette="deep", font="Hiragino Kaku Gothic Pro", font_scale=1, color_codes=False, rc=None):
fontの部分を日本語フォントに変えればよい。
KLダイバージェンスをそのまま可視化する
# 16×16次元のデータ
KLD = [ 95.31099625 91.15557772 56.59372546 112.20285226 94.41219084
211.66976101 92.55439072 121.40280516 99.87466514 76.50081387
176.93201868 91.81223113 85.27707457 105.14295556 125.49246929
130.92378707]
[ 61.39054933 94.3470823 ...
import seaborn as sns
import matplotlib.pyplot as plt
# X軸Y軸に表示する文字列
feature_names = ['%d' % i for i in range(KLD.shape[1])]
# 可視化
sns.heatmap(KLD, annot=False, xticklabels=feature_names, yticklabels=feature_names)
plt.show()
主成分分析していないので法則性がない。
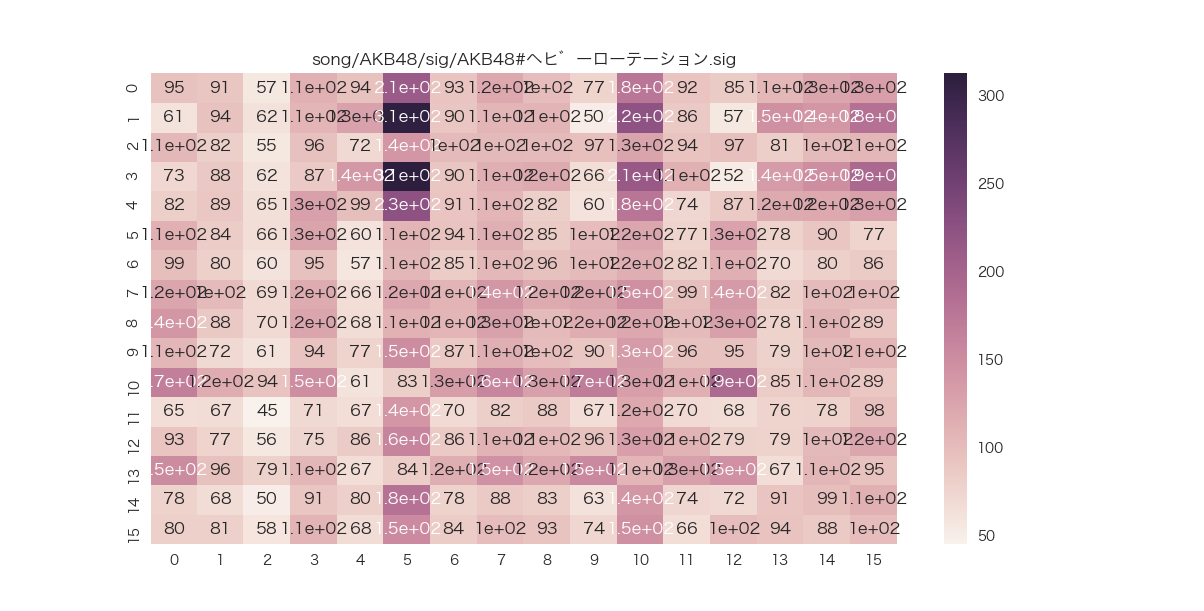
各次元での値も出力してみる。
# annotをTrueにすればOK
sns.heatmap(KLD, annot=True, xticklabels=feature_names, yticklabels=feature_names)
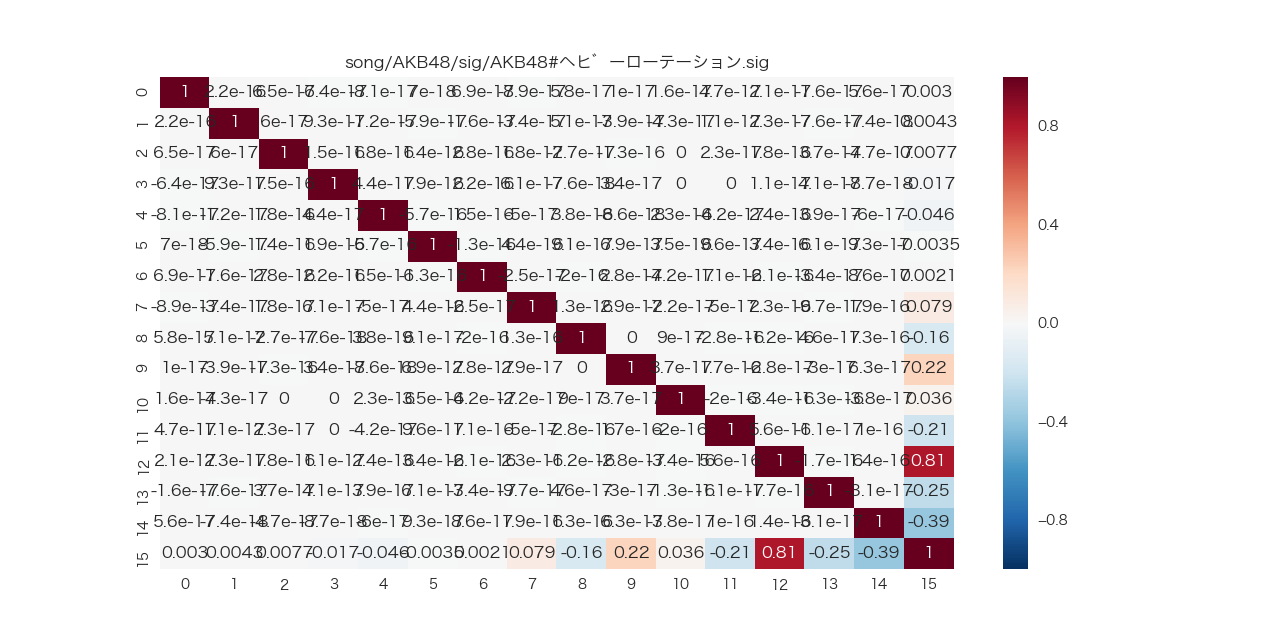
主成分分析して相関行列を可視化する
PCAという手法を使う
from sklearn.decomposition import PCA
import numpy as np
# n_componentsを指定しないとデータの次元数のまま分析される
pca = PCA()
pca.fit(KLD)
features = pca.fit_transform(KLD)
matrix = np.corrcoef(features.transpose())
sns.heatmap(matrix, annot=True, xticklabels=feature_names, yticklabels=feature_names)
plt.show()
対角成分がちゃんと全部1になった!
相関行列の特徴を満たしている。
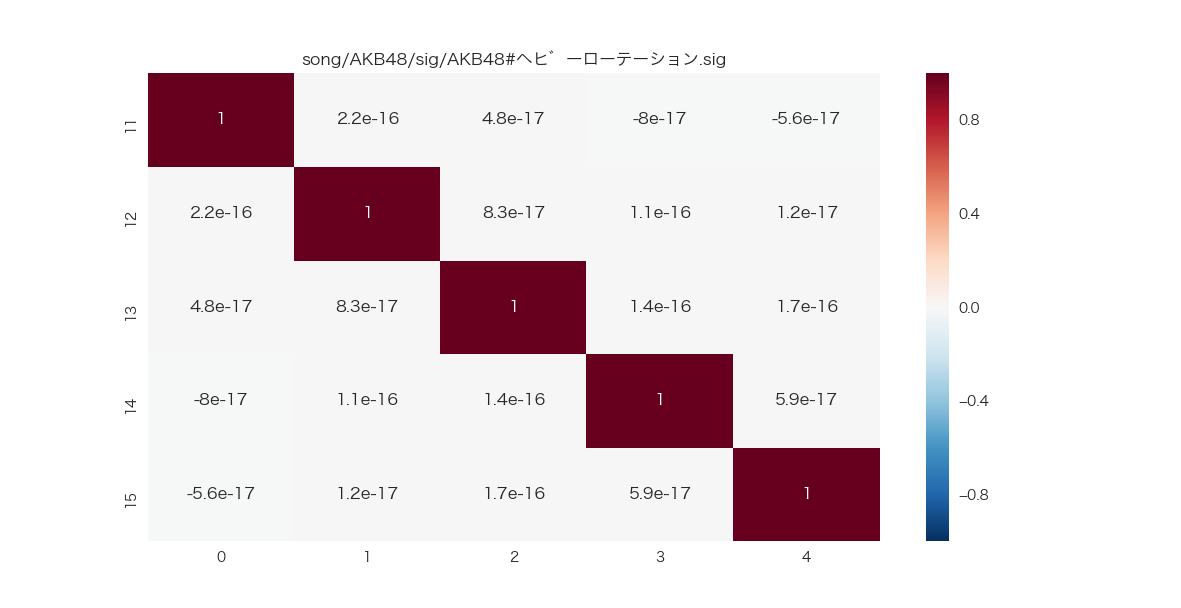
次元圧縮して主成分分析して可視化する
上記はそのまま16×16次元で主成分分析を行ったが
16×16だとさすがに多いので5×5に次元を落とす。
#n_componetsが次元数となる
pca = PCA(n_components=5)
見やすい。