はじめに
kaggleに掲載されているCredit Card Fraud Detection(URLは以下)のような問題の場合、誤識別は経済的損失を伴う。
https://www.kaggle.com/dalpozz/creditcardfraud
したがって、識別モデルの評価は識別精度に加えて経済的損失を評価対象に加える必要がある。大抵は精度向上に反比例して経済的損失が低減するので精度を指標にモデルのチューニングを行えばよいことになるが、偽陽性と偽陰性で1件当たりの経済的損失が異なるような場合、精度向上によって全体の経済的損失が大きくなることが起こる。
これは、識別モデルのパラメータが精度を基準に最適化され、識別の結果がもたらす経済的損失が考慮されていないことに起因する。言い換えると、パラメータ決定プロセスに経済的損失を考慮するようなコードを組み入れることができれば、モデルは経済的損失を適正にするものになると思われる。そこで、本論はこうした問題意識のもと、識別モデルパラメータ決定プロセスに経済的損失を反映するコードを検討する。
前提
検討にあたって使用する環境は以下の通りである。
OS : Windows10
言語: python 3.6系
: tensorflow 1.2.1
tensorflowはアップデートしてpython3.6系にも対応するようになったのでこのバージョンを使用している。なお、公式サイトのインストール方法は3.5系にインストールするものなので、その方法は別の情報ソースにあたる必要がある。以下に自分が参考にしたURLを掲載する。
https://stackoverflow.com/questions/43419795/how-to-install-tensorflow-on-anaconda-python-3-6
また、検討の対象とするモデルはtensorflow上で作成するニューラルネットワークとし、2値分類問題を対象とする。
経済的損失の反映方法の検討
tensorflowの入門書の2値分類のコードによると、モデルのパラメータは以下のプロセスで決定される。
ステップ(1) :モデルが出力した結果をもとにsigmoid関数によってクラス1の確からしさを計算する。
ステップ(2) :ステップ(1)の結果よりモデルの精度の悪さの評価を行う。
ステップ(3) :Optimizerによってステップ(2)の結果を最小化するようにパラメータを更新する。
ステップ(4) ;所定の条件を満たすまで、ステップ(1)に戻って繰り返す。
これより、モデルパラメータは、「精度の悪さ」を基準に最適化が図られていることがわかる。したがって、このステップ(2)に経済的損失を考慮した評価結果を算出できれば、その結果をもとにOptimizerが適正なパラメータを探索することが期待できる。
この経済的損失の評価値であるが、識別の結果が一定の確率で誤りが生じ、その際の損失額がわかっているとすると、期待値の考え方より「誤りの発生確率×損失額」によってあらわすことができる。この誤りの発生確率は、先のプロセスにおけるステップ(1)で計算された確からしさをクラス1である確率と解釈して「1-確率」を誤りの確率として計算していることから、ステップ(2)でこの確率に損失額を乗算すれば損失の期待値が計算できることになる。
オリジナルのコスト関数(ステップ(2)の総称)は、以下のコードで表現される。
cost = -tf.reduce_sum(Y*tf.log(p0) + (1-Y)*tf.log(1-p0))
ここでいうp0は、識別モデルの出力結果をsigmoid関数によってクラス1である確からしさ(確率)にしたものである。したがって、p0はラベル0を1と間違える確率であり、1-p0はラベル1を0と間違える確率を意味することから、この値に誤識別による経済的損失を乗算すれば、モデルの経済的損失の期待値を計算することができる。
その際、tf.logというlog関数の扱いであるが、識別の誤りの発生確率を誤ったデータの含まれる割合をエントロピーという指標に変換するためのものであることからそのまま活かすことにする。log関数を活かした場合、適用対象は0から1の間の値をする必要があることから任意の正数を採る損失額はlog関数を適用後に乗算する。
コードの作成
次にコードの作成に移る。
二値分類問題の対象としてkaggleに掲載される「Credit Card Fraud Detection」とする。このデータセットは、一定期間のクレジットカード取引の履歴であり、不正取引か否かを表すClass・取引の特徴量(PCAによって数値化されたもの)・取引金額が含まれる。そこで、特徴量からClassを識別するモデルを作成した上、先の考え方に基づきコスト関数に経済的損失を加味したものにする。
なお、識別モデルは隠れ層のないものとする。また、経済的損失は取引金額とする。
以上をtensorflowにてモデル化したものは以下の通りである。
X = tf.placeholder(tf.float32,[None,28]) # 特徴量
Y = tf.placeholder(tf.float32,[None, 1]) # ラベル
L = tf.placeholder(tf.float32,[None ,1]) # 経済的損失
w0 = tf.Variable(tf.zeros([28,1]))
b0 = tf.Variable(tf.zeros([1]))
f0 = tf.matmul(X,w0) + b0
p0 = tf.sigmoid(f0)
cost = -tf.reduce_sum(Y*tf.log(p0)*L + (1-Y)*tf.log(1-p0)*L) # コスト関数
train_step = tf.train.AdamOptimizer().minimize(cost) # 最適化
外部から与えられる変数を定義するplaceholderに、従来の特徴量とラベルに加えて経済的損失を適用している。また、コスト関数を先の考察を踏まえた形態に変更している。オプティマイザーは学習率の考慮を必要としないAdamを使用した。
実験データの生成
今回は、経済的損失を考慮した損失関数を用いて学習させた識別モデルとオリジナルとの相違から有用性を確認する。そのため、Kaggleのデータをもとに次のテストケースを満たすデータを抽出・加工する。
ケース1 : 利用金額(Amount)をすべて1に置き換える。
経済的損失がすべて1なので、実質的にはオリジナルのコスト関数と異ならない。したがって、識別結果についてもオリジナルと異ならないはずである。
ケース2 : クラス0とクラス1の利用金額の分布を同一にする。
ケース3 : クラス0の利用金額の分布をクラス1より小さくする。
ケース4 : クラス1の利用金額の分布をクラス0よりも小さくする。
いずれのケースもオリジナルのものよりも経済的損失を考慮した学習のモデルのほうが、経済的損失は小さくなることが期待される。
元のデータは、クラス1(不正取引)の比率が全体の0.172%と不均衡である。この比率を保ったまま学習させると比率の小さいクラス1の精度を悪化させる方向に進んでしまうため、両者の件数を同一となるように調整することで件数の影響を排除する。
データ生成のコードは以下の通りである。
# test dataの作成
# Case1 : Amount=1
tmp01 = dat01_not_fraud.sample(len(dat01_fraud))
train01 = pd.concat([tmp01,dat01_fraud])
train01['Amount']=1
# Case2 : Class0とClass1のAmountを同一化
tmp01 = dat01_not_fraud.sample(len(dat01_fraud))
tmp01['Amount'] = dat01_fraud['Amount'].as_matrix()
train02 = pd.concat([tmp01,dat01_fraud])
# Case3 : Class0をClass1のAmountより小さい分布とする
tmp01 = dat01_not_fraud[dat01_not_fraud['Amount'] < dat01_fraud['Amount'].describe().loc['max']]
tmp01 = tmp01.sample(len(dat01_fraud))
train03 = pd.concat([tmp01,dat01_fraud])
# Case4 : Class0をClass1のAmountより大きい分布とする
tmp01 = dat01_not_fraud[dat01_not_fraud['Amount'] > dat01_fraud['Amount'].describe().loc['50%']]
tmp01 = tmp01.sample(len(dat01_fraud))
train04 = pd.concat([tmp01,dat01_fraud])
結果
実験結果は以下の通りである。
Case1(オリジナル)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 401.0 | 91.0 | 492.0 |
| 1 | 25.0 | 467.0 | 492.0 |
| All | 426.0 | 558.0 | 984.0 |
Case2(カスタム)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 401.0 | 91.0 | 492.0 |
| 1 | 25.0 | 467.0 | 492.0 |
| All | 426.0 | 558.0 | 984.0 |
予想通りに同一の結果となった。
Case2(オリジナル)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 50448.20 | 9679.77 | 60127.97 |
| 1 | 5197.87 | 54930.10 | 60127.97 |
| All | 55646.07 | 64609.87 | 120255.94 |
Case2(カスタム)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 51186.78 | 8941.19 | 60127.97 |
| 1 | 1850.11 | 58277.86 | 60127.97 |
| All | 53036.89 | 67219.05 | 120255.94 |
経済的損失を抑制する方向にパラメータが収束している。特にクラス1(不正取引)を正当取引を誤識別するケースについては損失が大幅に減少している。
Case3(オリジナル)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 37334.60 | 8326.61 | 45661.21 |
| 1 | 2980.02 | 57147.95 | 60127.97 |
| All | 40314.62 | 65474.56 | 105789.18 |
Case3(カスタム)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 41725.02 | 3936.19 | 45661.21 |
| 1 | 6033.15 | 54094.82 | 60127.97 |
| All | 47758.17 | 58031.01 | 105789.18 |
損失の総額は、オリジナルの11,306から9,969に減少しているものの、1件あたり平均損失額が大きいクラス1の損失額が2倍程度に増加している。これは、Class1の利用金額(Amount)の分布による部分が大きい。以下は、Class1の利用金額と誤識別となったデータの利用金額をヒストグラム化したものである。
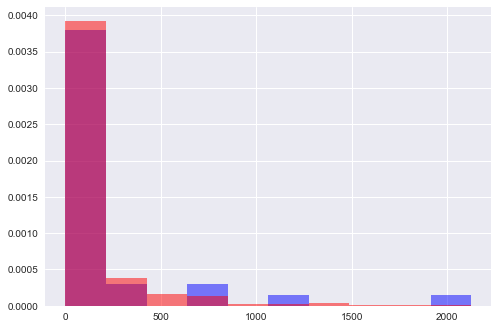
これから、誤識別に占める高額利用者の割合が大きいことがわかる。つまり、これらのデータの存在が想定と異なる結果をもたらしたものと思われる。
Case4(オリジナル)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 53902.08 | 10529.15 | 64431.23 |
| 1 | 4572.11 | 55555.86 | 60127.97 |
| All | 58474.19 | 66085.01 | 124559.20 |
Case4(カスタム)
| Predict | 0 | 1 | All |
|---|---|---|---|
| Class | |||
| 0 | 58051.46 | 6379.77 | 64431.23 |
| 1 | 8321.70 | 51806.27 | 60127.97 |
| All | 66373.16 | 58186.04 | 124559.20 |
損失総額は、オリジナルと差がない。クラス0のデータはランダムに抽出しているので、複数回実施してみたところ、カスタムしたほうが損失額が大きくなることもあり、期待した通りとは言い切れない。ただし、これについても利用金額の大きいデータの誤識別が影響したものである。
Case3およびCase4の結果からいうと、今回のコスト関数のようにデータ1件単位に損失額を設定する方式の場合、その金額の多寡がトータル金額に大きく影響してしまい、経済的損失を最小化するモデルパラメータの設定とならないケースがありうる。
なお、確認のために混合行列を算出して偽陽性・偽陰性を件数を算出したところ、オリジナルよりもカスタムしたほうが精度が向上しており、コスト関数に経済的損失を考慮することは一定の効果が期待できる。
まとめ
コスト関数に経済的損失を考慮して学習を進めた場合、個々のデータに割り当てられる損失額(今回のテストでいうと利用金額)の分散が大きいと1件の誤識別が与える影響が大きくなり、データによっては期待した成果が得られない。しかしながら、誤識別データの特徴量をもとにモデルのチューニングを図ることができれば、期待した成果が上げられると思われる。