Zabbix Advent Calendar 2015 最後の記事です。
皆様、MerryChristmas!!
Zabbix 3.0 を運んできてくれるサンタさんは残念ながら居なかったのですが
Zabbix 3.0 の目玉機能である、予測機能について考えましょう。
※現時点でのZabbix3.0 マニュアルを元にしています。
正式リリースまでに変更される可能性があります。
Zabbix3.0 予測機能とは
Zabbix3.0 の予測機能とは、トリガー関数に新たに導入される
forecast 関数によって実現されます。
原理としては「最小二乗法による近似曲線の延長による未来時点の数値予測」になります。
細かな用語については統計学や線形代数、大学の物理学実験の初等レベル数学が必要となります。
実際に設定する際の関数書式は次の通りとなります。
forecast (sec|#num,<time_shift>,time,<fit>,<mode>)
それぞれの引数について見ていきましょう。
sec|#num
これまでのmaxやavg関数と同様、関数の評価に利用するアイテムの時間もしくは個数になります。
<time_shift>
avg関数と同様、過去の時点でのsec|#numを利用したい場合に、指定するパラーメータになります。
オプションパラメータですので、省略した場合は、判定時点を元にsec|#numの値が評価されます。
たとえば前日のデータを元に予測するような場合に設定します。
time
何時間後のデータを予測するかを指定します。
<fit>
予測に使用する関数型を指定します。
予測には、linear,polynomialN,exponential,logarithmic,power
が使用できます。省略した場合はlinearになります。
この部分については、後ほど詳細に見ていきます。
<mode>
予測の出力形式になります。
value,max,min,delta,avg
オプションパラメータであり、指定しなかった場合はvalueとなります。
予測機能では単純に増加/減少だけではなく、振動するようなデータも予測することができます。
| mode | 計算式 | 解説 |
|---|---|---|
| value | f(now + time) | timeで指定された未来時刻での値を示します |
| max | maxnow <= t <= now + time f(t) | 現在からtimeで指定された未来時刻までの間の最大値を示します |
| min | minnow <= t <= now + time f(t) | 現在からtimeで指定された未来時刻までの間の最小値を示します |
| delta | max - min | 現在からtimeで指定された未来時刻までの間での最大値と最小値の差を示します |
| avg | average of f(t) (now <= t <= now + time) according to definition | 現在からtimeで指定された未来時刻までの間の平均値を示します。 |
| ※f(t)というは、時刻tによって値が決定される任意の関数fという意味になります。 | ||
| ※※ここで言う関数とは、プログラミングにおける関数ではなく、 | ||
| 数学的な意味合いでの関数のことになります。 |
fitについて
オプションパラメータであるfitには
linear,polynomialN,exponential,logarithmic,powerの種類があります。
この内容について、正しく理解するには、線形代数、および統計についての理解が必要になります。
さて、ここまで読んで、回れ右しようと思った方、安心してください。
ちゃんと解説します。
Zabbix3.0のマニュアルページにも数式がのっていますが
変数の置き方が海外風ですので、日本の高校などでなじみがある書式で書き直しておきます。
| fit | 数式 | 解説 |
|---|---|---|
| linear | y = ax+b | 線形関数として横軸を伸ばした場合の縦軸の値を予測します |
| polynomialN | y = a0 + a1x + a2x^2 + … + an*x^n | Nの上限は6 6次までの一変数多項式として値を予測します、 |
| exponential | y = aexp(bx) | 指数関数として横軸を伸ばした場合の縦軸の値を予測します |
| logarithmic | y = a*log(x)+b | 対数関数として横軸の常用対数から縦軸を予測します |
| power | y = a*x^b | 累乗関数として、横軸をべき乗じたものが縦軸の値になる予測を行います |
「基本は線形」は正しいか
Zabbix カンファレンス Japanの発表でも有りましたが
「基本はlinearを使う」という選択は正しいです。
なぜなら、そもそもコンピュータに関する物理量(ディスク容量など)は線形に推移しますし、
CPU使用量やメモリ使用量などは周期変動はあっても、経過時間に依存して収束や発散することは無いからです。
しかしながら、それ以外の関数を使う場合、グラフを眺めてフィーリングで決定することは危険です。
数式的、物理的背景を理解すべきです。
fitについて(関数の解説)
それぞれの関数について解説します。
linear y=ax+b
高校の数学等でもよく見る一次関数です。
グラフをイメージして考えるとわかりやすいでしょう
yが縦軸の値、aがグラフを書いた場合の直線の傾き、bがx=0の場合の切片となります。
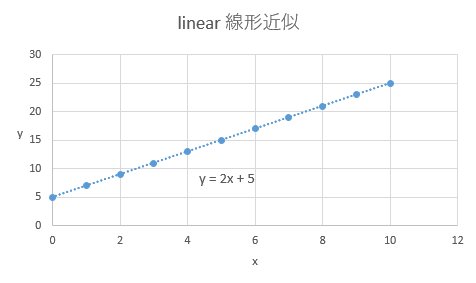
普通のグラフを書いたときに、直線となるのがlinear型、線形近似となります。
xつまり横軸はZabbixの場合時間軸になりますので、時間がたつにつれて一定の割合(このグラフの場合は2 一般化するとa ずつ増えて行くような関係性の場合この近似により、将来の値を推測することができます。
polynomialN (N=1~6) y = a0 + a1x + a2x^2 + … + an*x^n
多項式近似は特定の例示が存在しません。
増加、減少が一定で無いような曲線を描く場合に、無理矢理近似を行うのが多項式近似となります。
項数が増えるほど、曲線に近づきますが計算量は多くなります。
また、見た目が一致する可能性は上がりますが、数学的、物理的な意味はあまりありません。
exponential y = aexp(bx)
指数関数的と言われるように、Xの変化に対して急激に変化するグラフです。
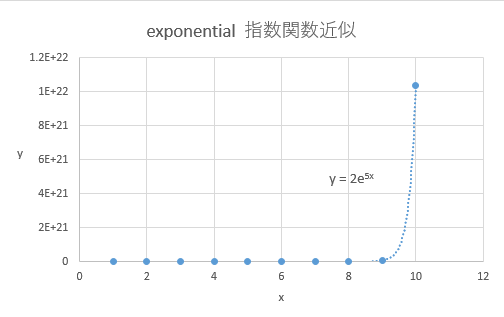
先程も説明しましたが、急激にカーブしている=指数関数
という判断は危険です。
指数関数の場合、グラフに対してちょっとした操作をすることによって、確認することが出来ます。
ヒストリデータをExcelに取り込み、縦軸の表示を対数表示にしましょう
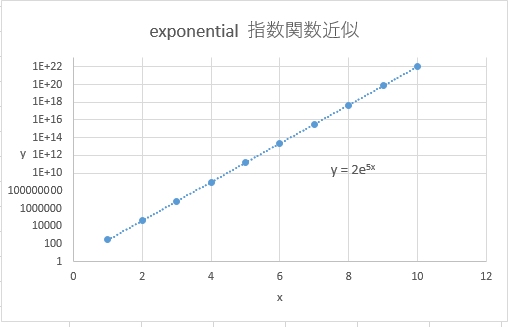
指数関数は片方の軸を対数目盛にすると直線となります。これを片対数グラフと言います。
さて、実際にこの関数を使うことはあるのでしょうか
指数関数的に増加するものはあまり思い浮かびません。
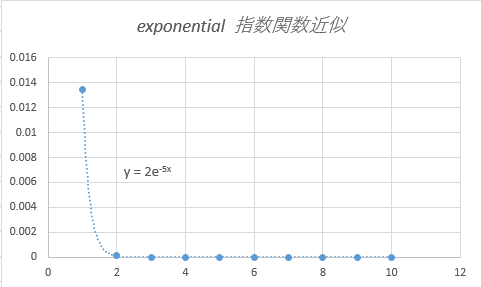
ただし、bの部分がマイナスになるものは指数関数的減衰として知られています。
指数関数的減衰は熱い物が冷めて行く際の温度変化などとして見られます。
Zabbix IoTなどでは、利用することがあるかもしれません。
logarithmic y = a*log(x)+b
指数と対数は反対の定義になりますので、指数関数グラフをちょうど180°ひっくり返したようなグラフになるのが対数関数になります。
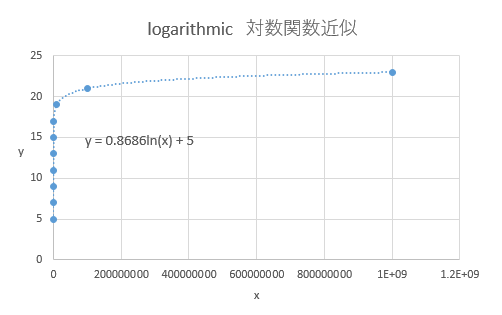
指数関数グラフでは縦軸を対数目盛にすることによって、直線となることが確認出来ましたが、対数関数の場合は、縦軸ではなく横軸(時間軸)を対数目盛にすると
やはり直線が現れます。
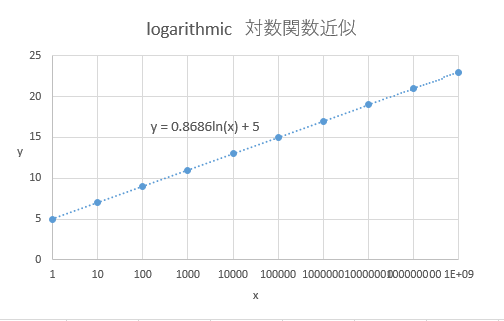
対数関数が現れる事象としては、疎密波とよばれる波の性質があります。
これは音波や地震波の計算に使われます。
これもIoTなどでは利用することになるかもしれません。
power y = a*x^b
縦軸の値が横軸のべき乗に従って変化する関数になります。
冪乗とか累乗という用語で語られます。
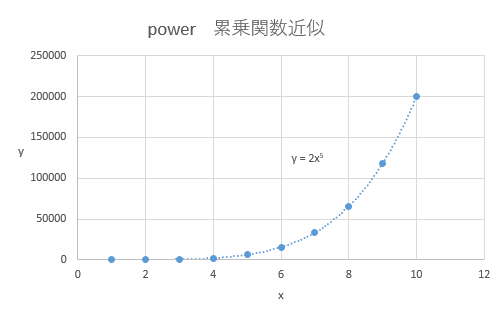
所謂曲線となりますが、今度は、縦軸も横軸も両方を対数目盛にしてみましょう
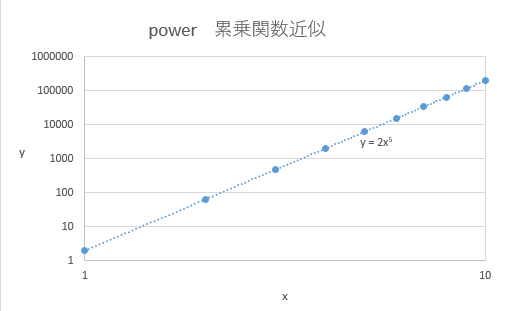
綺麗な直線が現れました、これを両対数グラフとよびます。
指数関数や対数関数どうよう、適用する際には実際にヒストリデータを抽出して両対数グラフにプロットしたさいに、直線になるかどうかを確認してから適用することをお奨めします。
さて、累乗が適用される領域ですが
経済物理学においては、資産分布や株価変動において、
自然科学では破損したかけらのサイズとその個数などが累乗関係に有ることが知られています。
で、実際使うの?
おそらくシステム監視という切り口で線形以外の関数を使うことは無いかもしれません。
しかしながら、Zabbix3.0では16日の記事でもあったとおり
Zabbix 3.0の新機能:ログファイルから数値を取得
ログからの数値取得も出来るようになっています。
ログからの数値解析や、IoT、マシンラーニングなどとの連携を行う用になった場合これらの関数が必要になるかもしれません。
そのときに、なんとなくの見た目では無く、上手く対数目盛を使い、
数式的に正しい事を確認されることをお奨めします。
Zabbixのforecast に実装されている関数はどれも
線形グラフ、片対数グラフ、両対数グラフのいずれかで描画すれば直線となる関数ですから、
実際の値を同じよう対数グラフで描画してみて、直線が現れないのであれば、その値はその関数ではFitしないことを意味します。
意外と重要なsec|#numパラメーター
システム監視であれば、おそらく線形関数のみであるというお話をしましたが、
線形関数を使う場合に1点注意が必要だとおもいます。
それは、ユーザ領域やログ領域のディスク使用量の場合、ユーザ数やアプリケーション数に比例してグラフの傾きが変化する可能性が高いと言うことです。
アプリケーション数については、インストール依存でしょうが
たとえばユーザ数依存のDBのサイズの場合、ユーザが増える毎に傾きが変化するようなグラフになるでしょう。この場合評価すべき数式自体は直線ですが、その傾きが刻々と変化する数値になります。
この場合評価する期間を短くすることで、傾きの変化を細かく再計算することが必要となるかもしれません。
あるいは、より長い期間の値を評価することで、長期的な傾きを得た方が予測が正確になるかもしれません。
forecast はavgやmax,min関数と事なり予測の数式だけで無く評価期間の選定も重要となります。
予測値が外れるという場合にはfitを変えるほかに、sec|#numの選定が重要となるかもしれません。
期待の新機能 Zabbixでデータサイエンティスト!
バズワードっぽくなりますが、Zabbixの予測機能は新しい可能性を提供する物だと思います。
Zabbixの予測機能は良い意味で単純ですから、グラフの意味を考えながら
データサイエンティストの仲間入りをしてみるのも良いのではないでしょうか。