[vDSP][信号処理]オーディオ・音声分析への道4 矩形波 ノコギリ波

オーディオ・音声分析への道4 矩形波 ノコギリ波

今回は、矩形波とノコギリ波を生成して、Libsndfileでwavファイルに書き出したいと思います。

矩形波

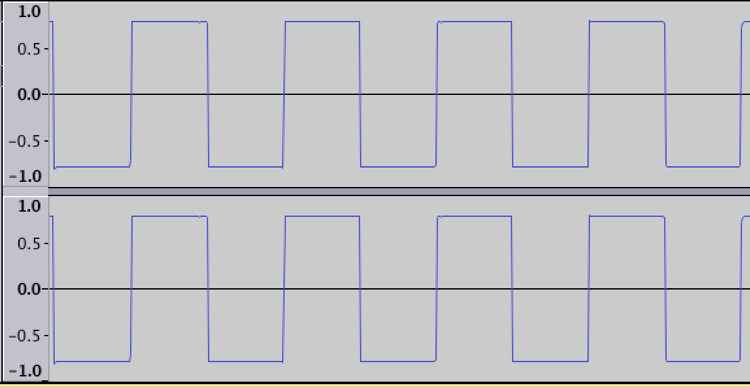
矩形波は波形で見ると四角い形をした波の事です。
これは、sin波を複数合成する事で近似の波を生成する事ができます。
矩形波を生成する為の式は、fを周波数(frequency)、mを音の大きさ（magnitude)とすると、

sin(f) + sin(f*3)/3 + sin(f*5)/5 + sin(f*7)/7 + sin(f*9)/9 ....

と半永久的に奇数倍した周波数のsin波の音量を同じ奇数で割ったもののを全て足し合わせた波になります。

実際的には、44100Hzのサンプリングレートで行う場合は、最大解像度が22050Hzなので、sin波の最高周波数が22050Hz以下になるように設定します。
ただし、この場合は計算に膨大な時間がかかるので今回は1000個くらいのsin波を合成することによって、近似波を生成したいと思います。

では全体のソースコードから

main.c

#include <stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#import"sndfile.h"
#define PAI 3.14159265358979323846264338 // PAI
#define SAMPLE_RATE 44100 //sampling rate
#define LENGTH 4 // 4 seconds
#define AMPLITUDE 1.0// 16bit
#define FREQUENCY 440 // frequency Hz
#define RESOLUTION 1000

int main(int argc, const char * argv[])
{

    //Libsndfile
    SNDFILE *fp;
    SF_INFO sfinfo;
    float *buffer;
    buffer = malloc(2*SAMPLE_RATE*LENGTH*sizeof(float));
    memset(&sfinfo,0,sizeof(sfinfo));

    sfinfo.samplerate = SAMPLE_RATE;
    sfinfo.frames = SAMPLE_RATE*LENGTH;
    sfinfo.channels = 2;
    sfinfo.format = (SF_FORMAT_WAV | SF_FORMAT_PCM_16);


    if(!(fp = sf_open("Sawtooth.wav", SFM_WRITE, &sfinfo))){
        printf("Error : Could not open output file .\n");
        return 1;
    }

    int i,j;

    for(i=0;i<SAMPLE_RATE*LENGTH;i++){ // STEREO

        float wav = 0;
        for(j=0;j<RESOLUTION;j++){
            wav += sin((float)FREQUENCY*(j*2+1) / SAMPLE_RATE * 2 * PAI *i)/(j*2+1);
        }
        buffer[2*i] = AMPLITUDE * (2/PAI) * wav;
        buffer[2*i+1] = AMPLITUDE * (2/PAI) * wav;
    }

    if(sf_write_float(fp, buffer,sfinfo.channels * SAMPLE_RATE*LENGTH)!= sfinfo.channels * SAMPLE_RATE*LENGTH)
        puts(sf_strerror (fp));

    sf_close(fp);
    return 0;
}

今回注目するのは、このコードのここだけです。

main.c

 for(i=0;i<SAMPLE_RATE*LENGTH;i++){ // STEREO
        float wav = 0;
        for(j=0;j<RESOLUTION;j++){
            wav += sin((float)FREQUENCY*(j*2+1) / SAMPLE_RATE * 2 * PAI *i)/(j*2+1);
        }
        buffer[2*i] = AMPLITUDE * wav;
        buffer[2*i+1] = AMPLITUDE * wav;
    }

その他は前回の記事を参考にしてください。
wav変数に奇数倍周波数のsin波/奇数倍をどんどん加算しています。
矩形波の数式は、wikipediaにて確認できます。

結果はこんな感じです。

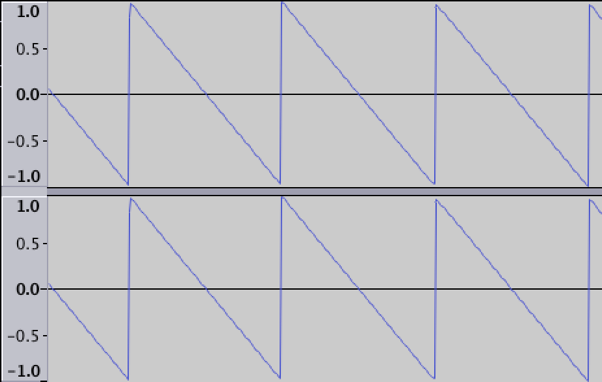
ノコギリ波

次はノコギリ波です。
ノコギリ波は段差1の等差数列で周波数を乗算、できたsin波の音量を除算し、すべてのsin波の総和です。

2/PAI * (sin(f) + sin(f*2)/2 + sin(f*3)/3 + sin(f*4)/4 + sin(f*5)/5 .... )

上のコードの、以下の部分を変更します。

main.c

float wav = 0;
for(j=0;j<RESOLUTION;j++){
    wav += sin((float)FREQUENCY*(j+1) / SAMPLE_RATE * 2 * PAI * i)/(j+1);
        }
    buffer[2*i] = AMPLITUDE * (2/PAI) * wav;
    buffer[2*i+1] = AMPLITUDE * (2/PAI) * wav;
        }

最後にbufferに格納する際、2/PAIを掛け合わせます。

波形を表示すると以下の通り。

RESOLUTIONを1000に設定すると結構処理時間がかかりますね。
200くらいが良いでしょうか。その代わり精度が落ちます。

vDSPで処理する

この二つの波形を使って、vDSPの関数を試してみたいと思います。
buffer以外に、もう一つbuffer2を作り、片方の波形をそこに格納します。

main.c

for(i=0;i<SAMPLE_RATE*LENGTH;i++){ // STEREO

        float wav = 0;
        float wav2 = 0;
        for(j=0;j<RESOLUTION;j++){

            wav += sin((float)FREQUENCY*(j*2+1) / SAMPLE_RATE * 2 * PAI * i)/(j*2+1);
            wav2 += sin((float)FREQUENCY*(j+1) / SAMPLE_RATE * 2 * PAI * i)/(j+1);

        }


    buffer[2*i] = AMPLITUDE * wav;
    buffer[2*i+1] = AMPLITUDE * wav;
    buffer2[2*i] = AMPLITUDE * (2/PAI) * wav2;
    buffer2[2*i+1] = AMPLITUDE * (2/PAI) * wav2;

 }

vDSP_vadd(buffer,1,buffer2,1,buffer,1,2*SAMPLE_RATE*LENGTH);

    float division = 2;
    vDSP_vsdiv(buffer, 1, &division, buffer, 1, 2*SAMPLE_RATE*LENGTH);

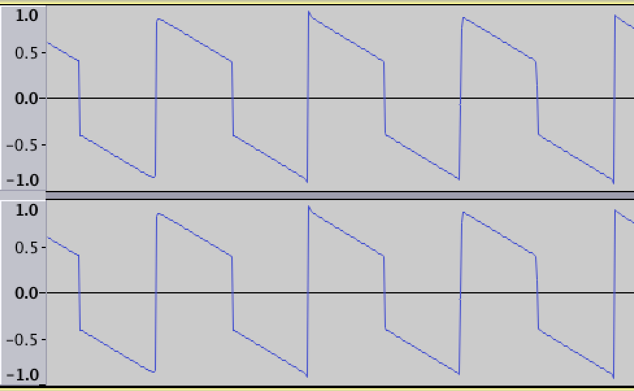
vDSP_vadd()で、二つの波形を加算します。これを加算合成と呼びます。
加算合成をすると、波形の強度（音の大きさ）がデータの最大値を超えてしまう事があるので、vDSP_vsdivにて2で割ります。

結果はこんな感じです。

なんかカッコいい感じになりました。

ではまた次回。