二次元偏微分方程式数値解 - 重力・空気抵抗あり膜の３Dシミュレーション -

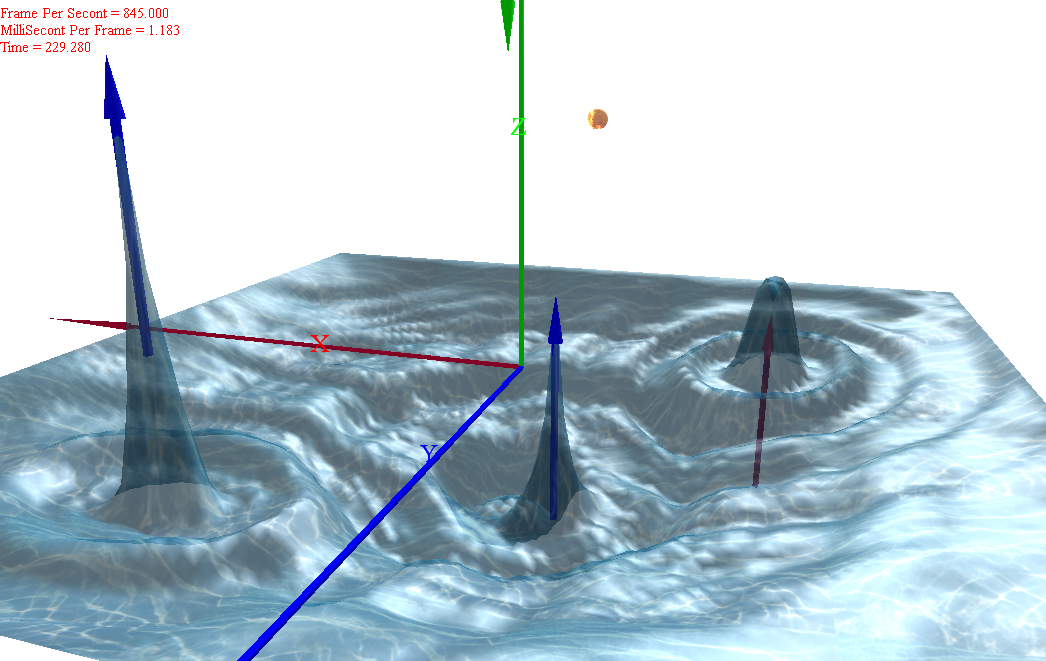
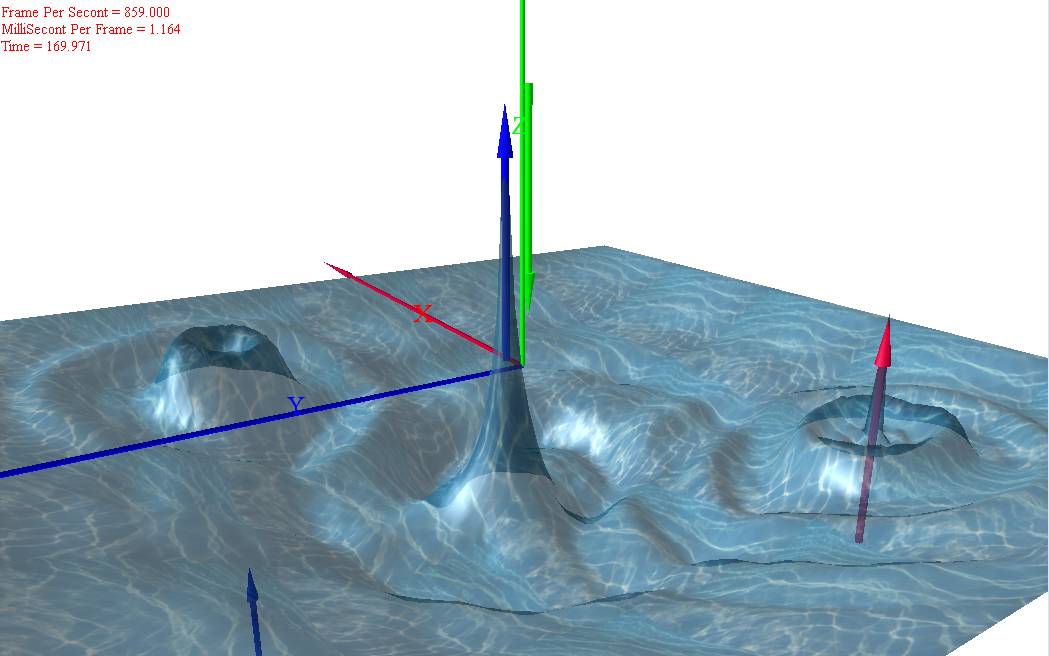
重力・空気抵抗項ありの二次元波動方程式の数値計算＆３D可視化

弦の振動の運動方程式から波動方程式導出(1次元)

\begin{eqnarray}
ρΔx\frac{∂^2u(x,t)}{∂^2t}&=&(Tsinθ_{x+Δx}-Tsinθ_x)-ρΔxg-kΔx\frac{∂u(x,t)}{∂t}\\
\end{eqnarray}

$ρ$ : 線密度
$T$ : 張力
$g$ : 重力加速度
$k$ : 抵抗係数
$θ_{〇}$ : $x=〇$での弦と$x$軸のなす角
右辺第1・2項は両端に働いてる張力の$u$方向成分、第3項は重力、第4項は速度に比例した抵抗
$θ$が小さいときは、$sinθ≒tanθ=\frac{∂u(x,t)}{∂x}$より

\begin{eqnarray}
ρΔx\frac{∂^2u(x,t)}{∂^2t}&≒&T(\frac{∂u(x+Δx,t)}{∂x}-\frac{∂u(x,t)}{∂x})-ρΔxg-kΔx\frac{∂u(x,t)}{∂t}\\
&≒&TΔx\frac{∂^2u(x,t)}{∂^2x}-ρΔxg-kΔx\frac{∂u(x,t)}{∂t}\\
\frac{∂^2u(x,t)}{∂^2t}&≒&\frac{T}{ρ}\frac{∂^2u(x,t)}{∂^2x}-g-\frac{k}{ρ}\frac{∂u(x,t)}{∂t}
\end{eqnarray}

2次元

\begin{eqnarray}
\frac{∂^2u(x,y,t)}{∂^2t}&≒&\frac{T}{ρ}(\frac{∂^2u(x,y,t)}{∂^2x}+\frac{∂^2u(x,y,t)}{∂^2y})-g-\frac{k}{ρ}\frac{∂u(x,y,t)}{∂t}
\end{eqnarray}

離散化

\begin{eqnarray}
\frac{1}{Δt^2}(u(t+Δt,x,y)+u(t-Δt,x,y)-2u(t,x,y))&=&\frac{1}{Δ^2}(u(t,x-Δ,y)+u(t,x+Δ,y)+u(t,x,y-Δ)+u(t,x,y+Δ)-4u(t,x,y))-g-\frac{k}{ρ}\frac{(u(t,x,y)-u(t-Δt,x,y))}{Δt}\\
u(t+Δt,x,y)&=&2u(t,x,y)-u(t-Δt,x,y)+\frac{Δt^2}{Δ^2}(u(t,x-Δ,y)+u(t,x+Δ,y)+u(t,x,y-Δ)+u(t,x,y+Δ)-4u(t,x,y))-Δt^2g-\frac{kΔt}{ρ}(u(t,x,y)-u(t-Δt,x,y))…①\\
(Δ=Δx=Δy)
\end{eqnarray}

今回の条件

・正方形の膜
・端は固定
・いくつかの場所に上下から振動しながら突き抜ける棒を設置

可視化

・動画

https://t.co/9NwPOwwIsX

— ぽんでりおん (@popondeli) 2017年6月23日

アルゴリズム

…
    //uの初期化
…
    //u(t,x,y)の更新
    for(int i = 1; i < MESH_NX-1; ++i) //端以外
    {
        for(int j = 1; j < MESH_NY-1; ++j) //端以外
        {
            u[t_index][i][j] = calcHeight(i, j, dt, mtime, t_index);
        }
    }
    //棒が突き抜けている位置は固定
    if (u[t_index][25][25] < 6.0f*sin(mtime))
        u[t_index][25][25] = 6.0f*sin(mtime);
    if (u[t_index][75][75] < -8.0f*cos(0.7f*mtime))
        u[t_index][75][75] = -8.0f*cos(0.7f*mtime);
    if (u[t_index][55][45] < -8.0f*cos(0.2f*mtime))
        u[t_index][55][45] = -8.0f*cos(0.2f*mtime);
    if (u[t_index][48][52] > 10.0f*cos(0.6f*mtime))
        u[t_index][48][52] = 10.0f*cos(0.6f*mtime);

    t_index++;
    if (t_index > 2)
        t_index = 0;
…

float calcHeight(int i, int j, float dt, float time, int t_index)
{
    float height;
    // height[t][x][y]、時間は2つ前(2Δt)のデータまで使用するため、t_indexを回して使いまわす。
    switch(t_index)
    {
    case 0:
        height = 2.0f*u[2][i][j] - u[1][i][j] + (TX*(u[2][i+1][j]-2.0f*u[2][i][j]+u[2][i-1][j]) + TY*(u[2][i][j+1]-2.0f*u[2][i][j]+u[2][i][j-1]))*dt*dt*0.2f + (FPerMass(i,j,time)*dt - K*(u[2][i][j]-u[1][i][j]))*dt;//①の計算
        break;
    case 1:
        height = 2.0f*u[0][i][j] - u[2][i][j] + (TX*(u[0][i+1][j]-2.0f*u[0][i][j]+u[0][i-1][j]) + TY*(u[0][i][j+1]-2.0f*u[0][i][j]+u[0][i][j-1]))*dt*dt*0.2f + (FPerMass(i,j,time)*dt - K*(u[0][i][j]-u[2][i][j]))*dt;//①の計算
        break;
    case 2:
        height = 2.0f*u[1][i][j] - u[0][i][j] + (TX*(u[1][i+1][j]-2.0f*u[1][i][j]+u[1][i-1][j]) + TY*(u[1][i][j+1]-2.0f*u[1][i][j]+u[1][i][j-1]))*dt*dt*0.2f + (FPerMass(i,j,time)*dt - K*(u[1][i][j]-u[0][i][j]))*dt;//①の計算
        break;
    }
    return height;
}

float FPerMass(int i, int j, float t)
{
    return -0.02f;//重力
}