はじめに
最近、勉強会などで数学を専門とする方々とお会いする機会にたくさん恵まれています。
そんな中で私は、場の空気を一切読まないで、事あるごとにD言語D言語D言語くんと連呼しているため、恐れ多くも**「D言語さん」**というたいへん名誉ある愛称まで頂いてしまいました。
D言語はやっぱりまだまだ知名度が低くて、様々な分野の方が集まる勉強会でさえ、こんな素晴らしい言語に触れた事がない方が大半です……。
そこで、D言語くん連呼するだけに留まらず、D言語を使ってどんなプログラミング体験が得られるか、ちゃんと書いていこうと思いつきました。
ゼータ関数を描こう
で、何をしようかと色々考えたところ、どうもゼータ関数というものを描くと (数学者に) モテるらしいという噂を耳にしました。
私は数学にあまり馴染みのない人間なのでゼータ関数が何者かよくわからないのですが、ググったところ、tsujimotterさまの素晴らしいブログ記事を見つけました。
tsujimotterのノートブック
リーマンのゼータ関数で遊び倒そう (Ruby編)
これさえ読めばゼータ関数はバッチリ、おまけにRubyでの実装まで出来てしまいますね。私が改めて付け足せることはありません。
なお、tsujimotterさんはゼータ関数を愛するあまり、「食べられるゼータ関数」や3Dプリントしたゼータ関数といったアート作品まで産み出されているとのことです。
食べられるゼータ関数 by つじもったー [クックパッド] 簡単おいしいみんなのレシピが203万品
というわけで、こんなゼータ関数を、D言語の使い方を紹介しながら調理してみます。
なお、読者には、C/C++やその他のプログラミング言語の基本的な知識があることを想定しています。
今回のソースコード
いきなり完成形を見せてしまいますが、ソースコードはこちらに置いてあります。
コミット履歴も記事の内容に合わせてタグを打ちながら入れてあるので、気になる方は見てみてください。
D言語セットアップ
DMDのインストール
D言語の処理系のインストールは超簡単です。
以下のURLから、自分の環境に適したDMDをダウンロードしてインストールしましょう。
今すぐに。
ほんの20MB弱ダウンロードして、インストーラ動かすなりzip展開するだけの手間です。昨今の巨大化した開発環境のダウンロードやらインストールやら初期設定と比べると、あたかも風に舞うタンポポの綿毛のごとく身軽です。軽快なポーズのD言語くん画像は伊達じゃありません。
dmdは、windowsでもMacでもLinuxでも同じくらいちゃんと動きます。私はここではMacを使っています。
windowsの場合は、64bitバイナリ生成のために事前にVisual Studioをインストールすることが推奨されますが、とりあえず試すだけなら無しでも大丈夫です。
DUBのインストール
パッケージマネージャであるdubのインストールも行います。
こちらもたかだか2MB弱のバイナリ1つに過ぎず、昨今の巨大化し(中略)せん。こちらも是非インストールしましょう。
今すぐに。
helloworld.d
さて、D言語はC/C++の流儀を引き継いだ、普通の実行ファイルを作れる古典的なコンパイラ言語です。つまり、D言語で作ったアプリは、特別なツールや実行環境を準備しなくても直接実行できます。(もちろん、特殊な動的ライブラリを参照した場合、その配布は必要です……)
D言語のHelloworldは以下のような感じです。
import std.stdio;
void main() {
writefln("hello,world!");
}
コンパイルします。すでにDMDをインストールしてパスも通っているあなたには余裕の作業です。
$ dmd helloworld.d
$ ls
helloworld helloworld.d helloworld.o
$ ./helloworld
hello,world!
このhelloworldは、特別なライブラリや環境を何もインストールしていない別のマシンで動作可能です。ただの実行ファイルだから当然です。(OSが違ったりするともちろん無理ですが……)
プロジェクトを作る
D言語のソースを書いてコンパイルするのは上記の通り難しくないのですが、ソースファイルが増えてきたりすると、shを書いたり、いにしえのMakefileを書いたりすることになったりします。
しかし、あなたがすでにインストールしてパスも通っているdubを使えば、ごく簡単に、複数のソースファイルからなるプロジェクトを作ることができます。
適当なディレクトリを掘って、以下のようにdubプロジェクトとして初期化します。
$ mkdir zeta1
$ cd zeta1
$ dub init
Successfully created an empty project in '/Users/dlangkun/zeta1'.
$ find . #何ができたか確認
.
./.gitignore # *.oとか無視する.gitignore
./dub.sdl # これはプロジェクトの設定ファイル
./source # ソースディレクトリ
./source/app.d # main関数のあるソース
app.dの中身はこんな感じです。つまりhelloworldです。
import std.stdio;
void main()
{
writeln("Edit source/app.d to start your project.");
}
ビルド・実行もdubを使って行えます。
$ dub
Performing "debug" build using dmd for x86_64.
zeta ~master: building configuration "application"...
Linking...
Running ./zeta1
Edit source/app.d to start your project. # これはapp.dの実行結果
この状態でsourceディレクトリ内にさらなる*.dファイルを追加しても、自動でコンパイル・リンクしてくれます。
module zeta;
string testZeta() {
return "zeta!";
}
import std.stdio;
import zeta;
void main()
{
writeln(testZeta());
}
$ dub
Performing "debug" build using dmd for x86_64.
zeta ~master: building configuration "application"...
Linking...
Running ./zeta1
zeta!
はい動きました。まだ全然ゼータ関数の片鱗も見えませんが、人生そんなものでしょう。
D言語の文法とか(は細かく解説しません)
今まで少し見てきた通り、D言語はほとんどそのままC/C++の文法と同じです。C/C++やJava・C#などのいずれかの経験があれば、下記サイトを流し見たりしながら何となく使えると思われます。
本家リファレンス
k3kaimuさんによる日本語のマニュアル
ゼータ関数の式
さて、ようやくゼータ関数です。
ゼータ関数は、いろいろやるとこんな形になるらしいです。詳しくはもちろんtsujimotterさんのブログ記事をご参照ください。
\zeta(s) = \frac{1}{1 - 2^{1-s}} \sum_{m=1}^{\infty}2^{-m} \sum_{j=1}^{m}(-1)^{j-1} \binom {m-1}{j-1} j^{-s}
この式のsは複素数です。複素数とか私はあんまり使う機会が無いのでテンションが上がります。むしろ四元数の方が、Unityの回転操作とかで使っていて馴染みがあるかもしれません。無論ライブラリに全部お任せですが……。
D言語で計算
さていよいよD言語で計算するコードを書きます。まず紹介したいのが、D言語の実数計算です。
リアル充実
C/C++と同じように普通にfloatとかdoubleとか使えるわけですが、D言語ではそれに加えてrealが使えます。一部のC/C++処理系で拡張精度で使えるlong doubleとほぼ同様で、IntelのCPUではだいたい80bit精度になるようです。
例えば、以下のようなコードが書けます。
import std.stdio;
import std.math;
void main()
{
real 充実 = PI;
double 非リア = cast(double) PI;
writefln("%.19f", 充実);
writefln("%.19f", 非リア);
}
さて、このコードでD言語ではUTF-8の識別子が使えること、型キャストはcast(T)という形の演算子で行うことが分かりましたね。キャストがもうこれ以上ないほどcastで一目瞭然ですね。
ちなみにこの命名はネタでやっているだけなので、D言語が推奨しているわけでも一般的なわけでもありません。絶対に真似しないでください。正気を疑われます。
$ dub
Performing "debug" build using dmd for x86_64.
zeta ~master: target for configuration "application" is up to date.
To force a rebuild of up-to-date targets, run again with --force.
Running ./zeta1
3.1415926535897932385
3.1415926535897931160
real 充実の方は円周率が小数部18桁までちゃんと出ました。
有効桁として扱って良いのかはよくわかりません。
複素数の計算
D言語には組み込み型で複素数と虚数がありまーす。
import std.stdio;
void main()
{
ireal 虚実 = 1.0i;
writeln(虚実);
writeln(虚実^^2.0);
creal 複実 = 1.0 + 虚実;
writeln(複実);
writeln(複実^^2.0);
}
$ dub
Performing "debug" build using dmd for x86_64.
zeta ~master: building configuration "application"...
Linking...
Running ./zeta1
1i
-1
1+1i
0+2i
と書いたところ、**[将来的にはstd.complexという標準ライブラリに完全移行する](http://dlang.org/deprecate.html#Imaginary and complex types)**との事でした……。
まあぶっちゃけ妥当ですね。std.complexはもう使えます。
import std.stdio;
import std.complex;
void main() {
auto 虚実 = complex(0.0L, 1.0L);
writeln(虚実);
writeln(虚実^^2.0L);
auto 複実 = 1.0L + 虚実;
writeln(複実);
writeln(複実^^2.0L);
}
$ dub
Performing "debug" build using dmd for x86_64.
zeta ~master: target for configuration "application" is up to date.
To force a rebuild of up-to-date targets, run again with --force.
Running ./zeta1
0+1i
-1-5.42101e-20i
1+1i
-5.42101e-20+2i
結果が微妙に違うのが気になる……。
ちなみに、autoという型は、勝手に型推論してくれる「なんでも」型です。複素数はComplex!(real)みたいなめんどくさい型になってしまうので、autoで無精しました。複雑だ!(現実)
二項係数の計算
さて、相変わらずtsujimotterさんの素晴らしいブログ記事におんぶに抱っこなのですが、ゼータ関数を書くために二項係数を計算しなければならない。重ね重ね素晴らしいことに、tsujimotterさんのブログではこの高速な計算アルゴリズムまで公開されています。
最後のキャッシュで求める方法がなんか必要になるっぽいので、そちらも実装してみましょう。
module zeta;
import std.algorithm : min;
import std.bigint : BigInt;
/// BigIntの定数1
private immutable BIG_INT_ONE = BigInt(1);
/**
* Params:
* n = 2項係数の上の数字
* k = 2項係数の下の数字
* Returns:
* 2項係数の値
*/
BigInt binom(int n, int k) @safe
in {
assert(0 <= n);
assert(0 <= k);
assert(k <= n);
} body {
k = min(n, n - k);
if(k == 0) {
return BIG_INT_ONE;
}
return binom(n - 1, k - 1) * n / k;
}
はい、なんか新しいのがたくさん出てきましたね。
実行時のための定数定義
/// BigIntの定数1
private immutable BIG_INT_ONE = BigInt(1);
こちらは計算で使用する1を定義しています。理由は後述しますが、値がBigIntなので1回だけ1個だけ生成して使い回したくなり、ここで定数定義しました。
privateはこのモジュールの外には見えなくするという意味です。
次のimmutableが難しいのですが、これは実行中に不変の値である、ということです。絶対に変わりません。
基本的にはC/C++のconstをイメージしてもらえれば良いのですが、より厳密で、他にスレッドが動いていようが決して変わりません。変えられないようになっています。
他にC/C++流のconst・複数スレッドで共有されることを示すsharedがあります。D言語の型システムでもなかなか難しいところなので、詳しくは言語リファレンス参照です。
ちなみに、目ざとい人は定数定義の左辺に型名が無いことに気づいたと思います。immutableなどのアクセス属性 + 変数名 = 値; となっている場合、型はコンパイラが推論できるので、省略可能です。
関数定義
BigInt binom(int n, int k) @safe
の行がいわゆる関数定義です。今までのmainとかと比べると、後ろに変なものが付いていますね。
後ろの@safeは関数の属性です。**無くても動きます。**でも、これを付けることで、ポインタなどの怪しげな操作やC言語のシステム関数などを呼んでいないことを明記できて、使える場所が増えます。
D言語は関数に付けられる属性が色々あって、それで型システムの表現力を上げています。@nogcという、GCを使ってないことを末代まで保証する属性もあります。出、出ーwwwwGC否定故現代言語否定奴〜もmain() @nogcとかすればイチコロですね。色々使えなくなるけど。
戻り値のBigIntは、読んで字のごとく標準ライブラリの多倍長整数です。
2項係数の値は例えば300とかまで計算すると非常に大きな値になる(80桁くらい?)ため、普通の整数型では収まりません。
そこで、BigIntを使用して何桁でも収まるようにしています。
Rubyでは動的型変換&組み込みのBignumで自然と扱えているのですが、D言語ではちょっと意識しないといけませんね。
きれいなimport
importがなんとなくライブラリをimportしているというのはみなさんご存知と思いますが、今回はimportがちょっと違う形で出てきましたね。
import std.algorithm : min;
import std.bigint : BigInt;
これは、今回std.algorithmモジュールのminしか使ってないので、それだけimportしているということです。モジュールの中身のごく一部しか使用しない場合は、こうやってimportすると名前空間が汚れず、依存関係も明確になって、良い感じです。複数指定も可能です。
import std.algorithm : min, max, any;
契約プログラミング礼賛
さて、関数本体に出てくるこの書き方、
in {
assert(0 <= n);
assert(0 <= k);
assert(k <= n);
} body {
これはD言語の契約プログラミング機能というものです。inの部分は、引数が満たすべき条件を示しています。これは関数の仕様になります。数学で言えば定義域ということになると思います。
なんとなくこれに違反してしまうと、デバッグビルドでは例外が飛びます。
(言い忘れていたけれど、D言語には普通に例外があるのでした。Javaと大体同じ。ただしチェック例外は無し)
リリースビルドではこのチェックは取り除かれ、オーバーヘッドは無くなります。bodyの中はつまり関数本文です。
ちなみに、契約プログラミング機能としては他にout(戻り値)チェック、classやstructに付けられるinvariant(不変性)チェックがあります。invariantは、メンバ関数呼び出し・終了時点で毎回チェックされます。
好きなだけ書こうユニットテスト
さて関数は一気に書いてしまったのですが、これ本当に二項係数計算できるの? と疑問に思いますよね。元記事が完璧でも、私がミスってる可能性ありますもんね。
コードを書いたらすぐテストして確かめたい……。そんなあなたの不安に応えるために、D言語ではユニットテストが超簡単に書けるようになっています。
module zeta;
import std.algorithm : min;
import std.bigint : BigInt;
/// BigIntの定数1
private immutable BIG_INT_ONE = BigInt(1);
/**
* Params:
* n = 2項係数の上の数字
* k = 2項係数の下の数字
* Returns:
* 2項係数の値
*/
BigInt binom(int n, int k) @safe
in {
assert(0 <= n);
assert(0 <= k);
assert(k <= n);
} body {
k = min(n, n - k);
if(k == 0) {
return BIG_INT_ONE;
}
return binom(n - 1, k - 1) * n / k;
}
/// これがユニットテスト
unittest {
assert(binom(0, 0) == 1);
assert(binom(1, 0) == 1);
assert(binom(1, 1) == 1);
assert(binom(2, 0) == 1);
assert(binom(2, 1) == 2);
assert(binom(2, 2) == 1);
assert(binom(3, 0) == 1);
assert(binom(3, 1) == 3);
assert(binom(3, 2) == 3);
assert(binom(3, 3) == 1);
assert(binom(4, 0) == 1);
assert(binom(4, 1) == 4);
assert(binom(4, 2) == 6);
assert(binom(4, 3) == 4);
assert(binom(4, 4) == 1);
assert(binom(5, 0) == 1);
assert(binom(5, 1) == 5);
assert(binom(5, 2) == 10);
assert(binom(5, 3) == 10);
assert(binom(5, 4) == 5);
assert(binom(5, 5) == 1);
}
unittestと書けばユニットテストになります。他にツールもフレームワークもライブラリも追加ライブラリのimportも不要です。
テストの実行は、コンパイラでも簡単に行えるのですが、やはりdubを使うのが簡単です。
$ dub test
Generating test runner configuration '__test__library__' for 'library' (library).
Performing "unittest" build using dmd for x86_64.
zeta ~master: building configuration "__test__library__"...
Linking...
Running ./__test__library__
All unit tests have been run successfully
All unit tests have been run successfullyと出ているのが、ユニットテストを通過した証です。何か間違った場合は、下記のように出ます。
? dub test
Generating test runner configuration '__test__library__' for 'library' (library).
Performing "unittest" build using dmd for x86_64.
zeta ~master: building configuration "__test__library__"...
Linking...
Running ./__test__library__
core.exception.AssertError@source/zeta.d(15): Assertion failure
----------------
4 __test__library__ 0x0000000100937ad0 _d_assert + 104
5 __test__library__ 0x000000010092ab51 void zeta.__assert(int) + 41
6 __test__library__ 0x000000010092b243 pure nothrow @nogc @safe int zeta.binom!(int).binom(int, int) + 31
7 __test__library__ 0x000000010092b20e void zeta.__unittestL26_2() + 578
8 __test__library__ 0x000000010092aaf0 void zeta.__modtest() + 8
9 __test__library__ 0x000000010093863a int core.runtime.runModuleUnitTests().__foreachbody2(object.ModuleInfo*) + 62
10 __test__library__ 0x000000010092d88e int object.ModuleInfo.opApply(scope int delegate(object.ModuleInfo*)).__lambda2(immutable(object.ModuleInfo*)) + 34
11 __test__library__ 0x000000010094bfed int rt.minfo.moduleinfos_apply(scope int delegate(immutable(object.ModuleInfo*))).__foreachbody2(ref rt.sections_osx.SectionGroup) + 85
12 __test__library__ 0x000000010094bf78 int rt.minfo.moduleinfos_apply(scope int delegate(immutable(object.ModuleInfo*))) + 32
13 __test__library__ 0x000000010092d865 int object.ModuleInfo.opApply(scope int delegate(object.ModuleInfo*)) + 33
14 __test__library__ 0x00000001009384e5 runModuleUnitTests + 145
15 __test__library__ 0x000000010094860a void rt.dmain2._d_run_main(int, char**, extern (C) int function(char[][])*).runAll() + 22
16 __test__library__ 0x00000001009485b3 void rt.dmain2._d_run_main(int, char**, extern (C) int function(char[][])*).tryExec(scope void delegate()) + 55
17 __test__library__ 0x0000000100948505 _d_run_main + 497
18 __test__library__ 0x000000010092aae1 main + 33
19 libdyld.dylib 0x00007fff956285ac start + 0
20 ??? 0x0000000000000000 0x0 + 0
Program exited with code 1
ええーまあ起きたことが正確に報告されるのですが、まあ
core.exception.AssertError@source/zeta.d(15): Assertion failure
を見ればzeta.dの15行目でユニットテストが失敗していることがわかります。書きながら動かすユニットテストでは十分ですよね。
このユニットテストと契約プログラミング機能を活用して、バグが少ないプログラムをサクサク書いていけるわけです。そう、D言語ならね。
もちろん他の言語でも、色々ライブラリなりツールなりIDEを使えばできるのでしょう。しかし、このサクサクとしたプログラミング体験は、他では得難いものがあります。守られてるってカンジ。
メモ化
ところで、キャッシュ実現するとか言ってまだしてませんでした。D言語ではメモ化(キャッシュ)はこんな感じで行えます。
import std.functional : memoize;
BigInt binom(int n, int k) @safe
in {
assert(0 <= n);
assert(0 <= k);
assert(k <= n);
} body {
return memoize!(delegate BigInt(int l, int m) @safe {
m = min(l, l - m);
if(m == 0) {
return BIG_INT_ONE;
}
return binom(l - 1, m - 1) * l / m;
})(n, k);
}
delegate BigInt(T l, T m) @safe {/* ... */}の部分はローカル関数リテラルです。D言語はローカル関数も無名関数も自然に使えるのでした。
memoize!(...)のmemoizeは、標準ライブラリに含まれるテンプレート関数です。
!はテンプレートの引数を指定して実体化を明示的に行うための演算子です。memoizeにまず関数リテラルを渡して実体化(!)し、そうしてできた関数に改めて(n, k)を渡しています。
つまり、今回は関数をテンプレート引数に取って新しい関数を作っているのです。新しい関数は、機能としては元の関数と同じですが、引数を元に自動でメモ化(memoize、つまりキャッシュ)を行ってくれます。
メモ化も含めて、こんな色々変えてしまってちゃんと動くのか? ご安心ください。そのためのunittestです。
dub test
# (中略)
All unit tests have been run successfully.
はい、さっきと同じテストケースが全部通りました。安心ですね。
ゼータ関数の実装
二項係数の計算ができたので、これでゼータ関数本体に取り組めます。
\zeta(s) = \frac{1}{1 - 2^{1-s}} \sum_{m=1}^{\infty}2^{-m} \sum_{j=1}^{m}(-1)^{j-1} \binom {m-1}{j-1} j^{-s}
この中で実装に議論があるのは、**無限の総和(Σ)**を計算している部分です。無限回とか計算一生終わらないじゃん! が、この式は収束するので、とりあえずループしてみて変化率が小さくなってきたら計算を打ち切って良いとの事でした。
テストファースト
今回はテストファーストでゼータ関数を実装していきます。
テストファーストとは、まず失敗するユニットテストを書き、コードのインターフェイスと期待される結果を明確にしてから、実装を書いていく方法です。こうすることで、まず最初の実装を作り、その後に内部を改善していく(リファクタリング)することが容易になります。
テストケースの設定
ゼータ関数の零点の値は、下記サイトで公開されています。
こちらをピックアップして、空のゼータ関数実装とテストケースを書きましょう。もちろん、今はまだ絶対失敗します。
import std.complex : complex, Complex, abs;
import std.string : format;
/**
* ゼータ関数を計算する。
*
* Params:
* R = 実数型
* s = ゼータ関数の引数
*/
Complex!R ζ(R)(Complex!R s) @safe {
return s;
}
// 非自明な零点の虚数部の値
immutable ZEROS = [
14.134725141734693790457251983562470270784257115699243175685567460149L,
21.022039638771554992628479593896902777334340524902781754629520403587L,
25.010857580145688763213790992562821818659549672557996672496542006745L,
30.424876125859513210311897530584091320181560023715440180962146036993L,
32.935061587739189690662368964074903488812715603517039009280003440784L,
];
/// 零点で0になること
unittest {
foreach(t; ZEROS) {
immutable z = ζ(complex(0x1p-1L, t));
assert(abs(z) == 0.0L, format("abs(z) == %sでした……。", abs(z)));
}
}
とりあえず実行します。
$ dub test
Generating test runner configuration '__test__library__' for 'library' (library).
Performing "unittest" build using dmd for x86_64.
zeta ~master: building configuration "__test__library__"...
Linking...
Running ./__test__library__
core.exception.AssertError@source/zeta.d(97): abs(z) == 14.1436でした……。
おめでとう!テスト失敗!!
これでユニットテストがちゃんと失敗することが証明されました。めでたしめでたし。
最初の実装
もちろんまだ終われません。最初は本当にベタ書きで良いので、関数の中身を実装します。
/**
* ゼータ関数を計算する。
*
* Params:
* R = 実数型
* s = ゼータ関数の引数
* Returns:
* ゼータ関数の値
*/
Complex!R ζ(R)(Complex!R s) @safe {
alias typeof(s) Complex;
auto outerSum = Complex(0);
// とりあえず255回計算してみる。
foreach(m; 1 .. 255 + 1) {
auto innerSum = Complex(0);
// 1からmまで
foreach(j; 1 .. m + 1) {
innerSum += (-1.0L) ^^ (j - 1) * binom(m - 1, j - 1).toLong() * j ^^ (-s);
}
outerSum += 2.0L ^^ (-m) * innerSum;
}
return 1.0L / (1.0L - 2.0L ^^ (1.0L - s)) * outerSum;
}
immutable ZEROS = [
14.134725141734693790457251983562470270784257115699243175685567460149L,
21.022039638771554992628479593896902777334340524902781754629520403587L,
25.010857580145688763213790992562821818659549672557996672496542006745L,
30.424876125859513210311897530584091320181560023715440180962146036993L,
32.935061587739189690662368964074903488812715603517039009280003440784L,
];
unittest {
foreach(t; ZEROS) {
immutable z = ζ(complex(0.5L, t));
assert(abs(z) == 0.0L, format("abs(z) == %aでした……。", abs(z)));
}
}
幸いなことに、std.complexには複素数の累乗演算子も実装されていたので、式をほぼそのままコードに写すだけで実装できました。
$ dub test
Generating test runner configuration '__test__library__' for 'library' (library).
Performing "unittest" build using dmd for x86_64.
zeta ~master: building configuration "__test__library__"...
Linking...
Running ./__test__library__
core.exception.AssertError@source/zeta.d(106): abs(z) == 0x9.5a895c22735460ap-16でした……。
はい案の定失敗しました〜
そもそも、コンピューターで計算して正確に0になるわけが……。
mainに実装を追加して、一通り値を見てみましょう。
import std.stdio;
import std.complex : abs, complex;
import zeta : ZEROS, ζ;
void main() {
foreach(t; ZEROS) {
writefln("%1$g %1$a", abs(ζ(complex(0.5L, t))));
}
}
$ dub
Performing "debug" build using dmd for x86_64.
zeta1 ~master: building configuration "application"...
Linking...
Running ./zeta1
0.000142726 0x9.5a895c22735460ap-16
0.000210998 0xd.d3f5a8c3fbe4febp-16
0.000203148 0xd.504321acca1e03ap-16
9.51346e-05 0xc.782fa4b389bb804p-17
9.46224e-05 0xc.670085344464f1cp-17
言い忘れましたが、formatやwriteflnは、C言語で言うところのprintfで、似たような書式化文字列を使って値を出力できます。
中でも、%aという指定では、各種実数型を16進数 * 2^^nの形で出力できます。
コンピュータ内部の実数は基本的に2進数で0.0〜1.0の仮数部 * 2^^nの指数部の組み合わせで表現されているので、%aで出力した結果は誤差のない正確な表現になります。
コード上に直接書いても安心です。
さて、どの値も0とは言い切れませんが、だいたい小さい値になっているようです。これらの値をとりあえず正確なものとしてテストコードに組み込みましょう。
少なくとも今より精度が悪くなるような修正を行わないよう、計算結果の絶対値が今以下になるようunittestで強制します。
// 非自明な零点の虚数部の値
immutable ZEROS = [
[14.134725141734693790457251983562470270784257115699243175685567460149L, 0x9.5a895c22735460ap-16],
[21.022039638771554992628479593896902777334340524902781754629520403587L, 0xd.d3f5a8c3fbe4febp-16],
[25.010857580145688763213790992562821818659549672557996672496542006745L, 0xd.504321acca1e03ap-16],
[30.424876125859513210311897530584091320181560023715440180962146036993L, 0xc.782fa4b389bb804p-17],
[32.935061587739189690662368964074903488812715603517039009280003440784L, 0xc.670085344464f1cp-17],
];
/// 零点で0ぐらいになること
unittest {
foreach(t; ZEROS) {
immutable z = ζ(complex(0.5L, t[0]));
assert(abs(z) <= t[1], format("abs(z) == %aでした……。", abs(z)));
}
}
次はリファクタリング(内部構造の改善)を行っていきます。
シグマの定義
数学でよく使うΣが、現状ではforeachループで表現されています。良い機会なので、そのまま式の中で使えるΣ関数を作り、より数式に近い表現ができるようにしてみましょう。
D言語で普通にΣ的なものを実現すると、下記のようになります。
import std.algorithm : map, sum;
import std.range: iota;
unittest {
assert(iota(1, 10 + 1).map!(x => x).sum == 55);
assert(iota(1, 100 + 1).map!(x => x).sum == 5050);
}
これがこんな風になるときっと嬉しいです。
unittest {
assert(Σ(1, 10, x => x) == 55);
assert(Σ(1, 100, x => x) == 5050);
}
これを(ほぼ)実現するのは簡単で、元のコードを関数化すればOKです。
/**
* Params:
* T = 添字の型
* F = 実行する関数の型。添字が渡される。
* begin = 初期値
* end = 終端(この値まで含んで実行される)
* f = 実行される関数
* Retuns:
* fの結果の総和。型は総和の型。
*/
auto Σ(T, F)(T begin, T end, F f) @safe {
return iota(begin, end + 1).map!(f).sum;
}
もはや詳しくは説明しませんが、iotaはbegin〜end(endは含まない)の連番を生成する関数で、mapはその連番を順に関数fに渡す関数です。
関数fにより連番が別の数字に変換され、それがsumにより合計されます。
それぞれの関数やその他の範囲・アルゴリズム関連については、下記ページが一次資料です。
http://dlang.org/phobos/std_algorithm.html
http://dlang.org/phobos/std_range.html
これでほぼ思った通りのことが実現できますが、無名関数の型の類推がうまくいかないので、使うときには明示が必要です。
unittest {
assert(Σ(1, 10, (int x) => x) == 55);
assert(Σ(1, 100, (int x) => x) == 5050);
}
少し残念ですが、ちゃんと動くので、これでよしとしましょう。
これを使ってゼータ関数を書き直せます。
Complex!R ζ(R)(Complex!R s) @safe {
return 1.0L / (1.0L - 2.0L^^(1.0L - s))
* Σ(1, 255, (int m)
=> 2.0L^^(-m) * Σ(1, m, (int j)
=> (-1.0L)^^(j - 1) * binom(m - 1, j - 1).toLong() * j^^(-s)));
}
テストはちゃんと通ったので、機能としては前のコードと正確に一致します。
しかし、あまり読みやすくなってない気が……。
次回予告
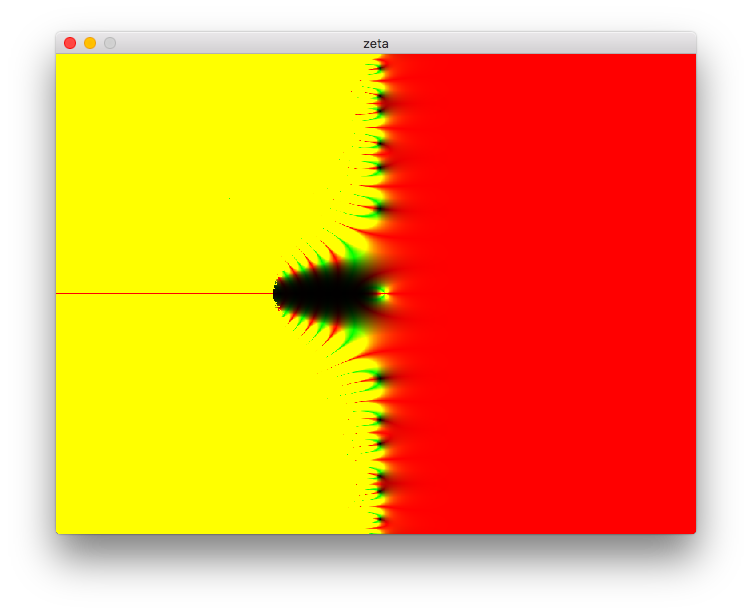
次回は SDL2 + OpenGL 4.0 でゼータ関数を可視化します。さらなる高速化も検討します。
こちらは試作イメージです。さらに進化する予定……。