Unity 4D - Unityで4次元を見てみよう
この記事は数学カフェ_4次元コンテンツ出展の記録 Advent Calendar 2016
の、12月7日分の記事です。
はしがき
いつも出入りさせて頂いている数学カフェで、サイエンスアゴラ2016というイベントへの企画出展にプログラマーとして参加しました。
UnityとOculusで4次元を見てみよう! というコンセプトで、本場の数学者の皆さんと一緒に仕事をする機会を得られて、とても楽しい作業でした。
この記事では、Unity + Oculusを使用した4次元描写についての技術的な知見をまとめてみようと思います。
なお、私はプライベートでは普段D言語しか書いていないような人間なのですが、今回はみんなのためにUnity + C# を駆使する必要性に駆られました。
4次元とは
理論的な枠組みについては、本ACの @miurror さんの各記事が詳しいです。
4次元というと時間 + 空間(3D)で4次元と言われることが多いですが、今回の企画では 空間次元を4つに拡張する という意味で使用されています。
つまり、縦(Y)・横(X)・前後(Z)に、 まったく新しい座標軸(W)が追加 されます。
その 4次元世界で起きることを、3次元人である我々にもVRで体感できるようにしよう! というのが、今回の企画のゴールです。
技術的問題
この腐敗した3次元の世界に4次元空間を落とし込むには、以下のような技術的問題があります。
Unityは3次元空間しか扱えない。どうやって4次元空間を扱うのか?
具体的には、
- カメラや物体の位置を記述する
Transformが3次元しかない - 物体の形状を記述する
Meshの頂点座標データが3次元しかない
人間は3次元人なので、最終的にはどうしても3次元に描画しなければならない
つまり、1次元分の情報は何かしらの方法で残り3次元に反映しなければならない。どう反映すればよいのか?
4次元の体感が得られるようになったとして、それをどう見せれば良いのか?
4次元の体感ができたとして、おそらく斬新で馴染みのないものになる。それをそのまま見せても理解が得られない可能性がある。どうやってそれを来場者に伝えれば良いのか?
技術的解決
私の担当はプログラマーなので、主に上記問題の1番目, 2番目(の技術面)に対応しました。
ざっと書くと、それぞれの解決策は下記のとおりです。
Unityは3次元座標しか扱えない
4次元座標を扱えるコンポーネントを追加した
-
Transformを拡張するTransform_4Dコンポーネントを作成した。 -
GameObjectが4次元分の座標+回転を持てるようにした。
4次元形状データをMeshで表現できるようにした
- 4次元形状データについては、独自のテキストフォーマットを開発した。
-
Meshに4次元分の頂点座標を持たせるため、uv1にW座標を埋め込んだ。
4次元の座標変換・描画を行うために、シェーダーでUnityの描画を拡張した
- 3Dの座標変換は通常4次元ベクトルや4次元行列を使用するが、それをすべて5次元で行うようにした。
- 生の座標変換をいろいろいじらなければならないので、Cg/HLSL使用
4次元を3次元に描画する
この問題については、@miurrouさんの記事で詳しく解説されています。
おおざっぱに言えば、4つ目の座標軸(W)の情報を両眼視差に反映することで4次元を体感させる という手法です。
UnityではHMD使用時に視差のパラメータを参照・調整できるので、視覚の左右それぞれで異なる画像を描画することが可能です。今回はそれを大いに活用しました。
実装
さて、ここからUnityでの実装について解説します。
実際のコードは、年内にもOSSライセンスでGithubで公開しようと考えています。その時には本記事をアップデートしてお伝えする予定です。
(企画出展したものは有料アセットを使用しているので、そのままではアップできないのでした……)
Transform_4D
まず、普通は3次元座標しか持たないGameObjectに4次元座標を与えられるようにします。これを行うことで、各種物体やカメラ・プレーヤー自身も4次元座標を持つことになります。
注意しなければならないのが回転で、**4次元では回転軸が6つになります。**軸周りの回転はXYZWのうち2つの座標軸を選んで値を変えることになるので、3次元では ${}_3\mathrm{C}_2$ で3つです。
しかし、4次元では ${}_4\mathrm{C}_2$ で6つになります。
using UnityEngine;
using System.Collections;
/// <summary>
/// 4次元座標コンポーネント
/// </summary>
public class Transform_4D : MonoBehaviour {
/// <summary>
/// W座標
/// </summary>
public float PositionW;
/// <summary>
/// W座標スケール
/// </summary>
public float ScaleW;
[Header("W軸の関わる回転")]
public float YZ;
public float XZ;
public float XY;
/// <summary>
/// モデル原点のワールド座標
/// </summary>
public Vector4 Position
{
get
{
// 3DのTransformの座標と組み合わせて4次元座標を返す
Vector3 position = transform.position;
return new Vector4(position.x, position.y, position.z, PositionW);
}
}
/// <summary>
/// モデルの向きを定める角度 XY XZ XW
/// </summary>
public Vector3 Rotation1
{
get
{
Vector3 angles = transform.rotation.eulerAngles;
return new Vector3(XY, XZ, angles.x);
}
set
{
XY = value.x;
XZ = value.y;
Vector3 angles = transform.rotation.eulerAngles;
angles.x = value.z;
transform.Rotate(angles);
}
}
/// <summary>
/// モデルの向きを定める角度 YZ YW ZW
/// </summary>
public Vector3 Rotation2
{
get
{
Vector3 angles = transform.rotation.eulerAngles;
return new Vector3(YZ, angles.y, angles.z);
}
set
{
YZ = value.x;
Vector3 angles = transform.rotation.eulerAngles;
angles.z = value.z;
angles.y = value.y;
transform.Rotate(angles);
}
}
/// <summary>
/// モデル各軸方向の拡大率
/// </summary>
public Vector4 Scale
{
get
{
Vector3 scale = transform.lossyScale;
return new Vector4(scale.x, scale.y, scale.z, ScaleW);
}
}
/// <summary>
/// 指定角度だけ回転する。
/// </summary>
/// <param name="rotation1">XY XZ XW</param>
/// <param name="rotation2">YZ YW ZW</param>
public void Rotate(Quaternion rotationXwYwZw, Quaternion rotationXyXzYz)
{
transform.rotation *= rotationXwYwZw;
Vector3 r = (Quaternion.Euler(XY, XZ, YZ) * rotationXyXzYz).eulerAngles;
XY = r.x;
XZ = r.y;
YZ = r.z;
}
}
Mesh4DController
次に、メッシュに4次元座標を格納し、シェーダーで4次元オブジェクトを描画できるようにします。
この時には、4次元の頂点座標に加えて、先ほどのTransform_4Dの情報も参照します。
using UnityEngine;
using System.Collections;
using System.Linq;
using cube4d.hobj; // 4次元形状データライブラリ
/// <summary>
/// 立方体コントローラークラス
/// </summary>
[RequireComponent(typeof(MeshRenderer))]
public class Mesh4DController : MonoBehaviour
{
// 中略
/// <summary>
/// オブジェクト形状のソースコード
/// </summary>
[SerializeField, Tooltip("オブジェクト形状のソースコード")]
public TextAsset objectSource;
// 4次元座標変換
private Transform_4D transform4d_;
// 生成されたメッシュオブジェクト
private Mesh mesh_;
/// <summary>
/// ゲーム開始時の処理
/// </summary>
void Awake()
{
transform4d_ = GetComponent<Transform_4D>();
// オブジェクト形状をテキストファイルから読み込む
HigherObject hobj = HigherObjects.ReadFromSource(objectSource.text).First().Value;
mesh_ = HigherObjects.MakeMesh(hobj);
}
/// <summary>
/// シーン開始時の処理
/// </summary>
void Start ()
{
// 読み込んだメッシュ情報を元にメッシュコンポーネントを追加
gameObject.AddComponent<MeshFilter>().mesh = mesh_;
}
}
4次元形状データは下記のようなフォーマットです。
これを頑張って解析するコードをC#で書きましたが、今考えたらJSONなどにすればよかった……。
### 立方体 ###
o Cube
### 頂点の定義 ###
# 手前の面
v -0.5 0.5 -0.5 0.0 / 1.0 0.0 0.0 0.3 # 0
v 0.5 0.5 -0.5 0.0 / 0.0 1.0 0.0 0.3 # 1
v 0.5 -0.5 -0.5 0.0 / 0.0 0.0 1.0 0.3 # 2
v -0.5 -0.5 -0.5 0.0 / 1.0 0.0 1.0 0.3 # 3
# 奥の面
v -0.5 0.5 0.5 0.0 / 1.0 1.0 0.0 0.3 # 4
v 0.5 0.5 0.5 0.0 / 0.0 1.0 1.0 0.3 # 5
v 0.5 -0.5 0.5 0.0 / 1.0 0.0 0.0 0.3 # 6
v -0.5 -0.5 0.5 0.0 / 0.0 0.0 0.0 0.3 # 7
### 面の定義 ###
# 手前の面
f 0 1 2
f 0 2 3
# 上面
f 0 4 5
f 0 5 1
# 下面
f 3 6 7
f 3 2 6
# 左面
f 0 7 4
f 0 3 7
# 右面
f 1 5 6
f 1 6 2
# 奥の面
f 4 7 6
f 4 6 5
Meshを生成する部分については下記のようになっています。
/// <summary>
/// HigherObjectからMeshを生成する。
/// </summary>
/// <param name="hobj">HigherObject</param>
/// <returns>HigherObjectから生成したMesh</returns>
public static Mesh MakeMesh(HigherObject hobj)
{
Mesh mesh = new Mesh();
// 名称設定
mesh.name = hobj.Name;
// 頂点配列の設定
mesh.vertices = hobj.Vertices.Select(v => new Vector3((float)v.x, (float)v.y, (float)v.z)).ToArray();
// W軸はUVに格納する
mesh.uv = hobj.Vertices.Select(v => new Vector2((float)v.w, 0.0f)).ToArray();
// 面の設定
mesh.triangles = hobj.Facets.SelectMany(f => new int[] { f.a, f.b, f.c }).ToArray();
if(mesh.triangles.Length == 0)
{
// 面が無ければ線の設定
mesh.SetIndices(hobj.Lines.SelectMany(l => new int[] {l.a, l.b}).ToArray(), MeshTopology.Lines, 0);
}
else
{
// 法線の計算
mesh.RecalculateNormals();
mesh.RecalculateBounds();
}
// 色の設定
mesh.colors = hobj.Vertices.Select(v =>
new Color((float)v.color.r, (float)v.color.g, (float)v.color.b, (float)v.color.a)).ToArray();
return mesh;
}
シェーダーでの4次元描画
先述の通り最終的には3次元描画に落とし込まなければならないのですが、そこまでは全て4次元で処理できます。
具体的には、3DCG描画のModel・View・Projection変換のうち、Model・Viewまでは4次元で行い、Projection変換で3次元に射影します。
その最後の射影の時点で、左右どちらのカメラに描画しているかの情報を使用し、差を出します。
まず、5次元行列の乗算などを行えるユーティリティメソッドを作成します。
/// 5次元行列
struct float5x5 {
float values[5][5];
};
/// 5次元ベクトル
struct float5 {
float values[5];
};
/// 5x5単位行列
static const float5x5 IDENTITY_5x5 = { {
{ 1.0f, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 1.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 1.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 1.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 1.0f },
} };
/// 5x5ゼロ行列
static const float5x5 ZERO_5x5 = { {
{ 0.0f, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 0.0f }
} };
/// ゼロベクトル
static const float5 ZERO_5x1 = { {0.0f, 0.0f, 0.0f, 0.0f, 0.0f} };
/// 5x5行列の乗算
float5x5 mul5x5(const float5x5 lhs, const float5x5 rhs)
{
float5x5 result;
for (int rhsCol = 0; rhsCol < 5; ++rhsCol)
{
for (int i = 0; i < 5; ++i)
{
float sum = 0.0f;
for (int j = 0; j < 5; ++j)
{
sum += (lhs.values[i][j] * rhs.values[j][rhsCol]);
}
result.values[i][rhsCol] = sum;
}
}
return result;
}
/// ベクトルと5x5行列の乗算
float5 mul1x5(const float5 lhs, const float5x5 rhs)
{
float5 result;
for (int rhsCol = 0; rhsCol < 5; ++rhsCol)
{
for (int j = 0; j < 5; ++j)
{
result.values[rhsCol] += (lhs.values[j] * rhs.values[j][rhsCol]);
}
}
return result;
}
/// 5x5行列とベクトルの乗算
float5 mul5x1(float5x5 lhs, float5 rhs)
{
float5 result = ZERO_5x1;
for (int i = 0; i < 5; ++i)
{
for (int j = 0; j < 5; ++j)
{
result.values[i] += (lhs.values[i][j] * rhs.values[j]);
}
}
return result;
}
これらを使って、4次元座標の平行移動・回転・スケーリングがおこなえるようにします。
/// スケーリング行列を生成する
float5x5 makeScale(float4 value)
{
const float5x5 result =
{ {
{ value.x, 0.0f, 0.0f, 0.0f, 0.0f },
{ 0.0f, value.y, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, value.z, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, value.w, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 1.0f },
} };
return result;
}
/// 平行移動行列を生成する
float5x5 makeTranslation(float4 value)
{
const float5x5 result =
{ {
{ 1.0f, 0.0f, 0.0f, 0.0f, value.x },
{ 0.0f, 1.0f, 0.0f, 0.0f, value.y },
{ 0.0f, 0.0f, 1.0f, 0.0f, value.z },
{ 0.0f, 0.0f, 0.0f, 1.0f, value.w },
{ 0.0f, 0.0f, 0.0f, 0.0f, 1.0f },
} };
return result;
}
/// ZW平面回転行列を生成する(XY座標が変化)
float5x5 makeRotateZW(float theta)
{
float c = cos(theta);
float s = sin(theta);
const float5x5 result =
{ {
{ c, -s, 0.0f, 0.0f, 0.0f },
{ s, c, 0.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 1.0f, 0.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 1.0f, 0.0f },
{ 0.0f, 0.0f, 0.0f, 0.0f, 1.0f },
} };
return result;
}
回転座標は、これに続けて5つあります(略)。
さて、ここからが一番気持ち悪いところなのですが、上記の各種行列を使用して、Model変換・View変換を行なっていきます。
/// モデル行列の生成
float5x5 makeModelMatrix(float4 scale, float4 rotation1, float4 rotation2, float4 translation)
{
const float5x5 xy = makeRotateXY(radians(rotation1.x));
const float5x5 xz = makeRotateXZ(radians(rotation1.y));
const float5x5 xw = makeRotateXW(radians(rotation1.z));
const float5x5 yz = makeRotateYZ(radians(rotation2.x));
const float5x5 yw = makeRotateYW(radians(rotation2.y));
const float5x5 zw = makeRotateZW(radians(rotation2.z));
const float5x5 r1 = mul5x5(xw, zw);
const float5x5 r2 = mul5x5(yw, r1);
const float5x5 r3 = mul5x5(xz, r2);
const float5x5 r4 = mul5x5(yz, r3);
const float5x5 rot = mul5x5(xy, r4);
const float5x5 s = makeScale(scale);
const float4 t = float4(translation.x, translation.y, -translation.z, translation.w); // z軸は反転する。(前が負の方向)
const float5x5 tr = makeTranslation(t);
const float5x5 rots = mul5x5(rot, s);
return mul5x5(tr, rots);
}
// モデル行列
static const float5x5 M = makeModelMatrix(_CubeScale, _CubeRotation1, _CubeRotation2, _CubePosition);
View変換については、カメラの視差による変換も同時に行なっています。
座標変換の方法について、まだTODOが残っています(汗)。
/// ビュー行列の生成
float5x5 makeViewMatrix(float4 rotation1, float4 rotation2, float4 translation, float separation, float convergence, float squint, int enable4d)
{
const float4 rot1 = float4(-rotation1.x, -rotation1.y, rotation1.z, 0.0f); // TODO: なぜここでxw軸回転は反転させなくてよいのか考える
const float4 rot2 = float4(-rotation2.x, rotation2.y, -rotation2.z, 0.0f); // TODO: なぜここでyw軸回転は反転させなくてよいのか考える
const float4 t = float4(-translation.x, -translation.y, translation.z, -translation.w); // z軸は反転する。(前が負の方向)
const float5x5 tr = makeTranslation(t);
const float5x5 xy = makeRotateXY(radians(rot1.x));
const float5x5 xz = makeRotateXZ(radians(rot1.y));
const float5x5 xw = makeRotateXW(radians(rot1.z));
const float5x5 yz = makeRotateYZ(radians(rot2.x));
const float5x5 yw = makeRotateYW(radians(rot2.y));
const float5x5 zw = makeRotateZW(radians(rot2.z));
const float5x5 r1 = mul5x5(yz, xy);
const float5x5 r2 = mul5x5(xz, r1);
const float5x5 r3 = mul5x5(yw, r2);
const float5x5 r4 = mul5x5(xw, r3);
const float5x5 rot = mul5x5(zw, r4);
const float5x5 worldView = mul5x5(rot, tr); // 移動してから回転
// 右目の場合 tan = +sep / convで atan > 0 になる。
// 左目の場合 tan = -sep / convで atan < 0 になる。
// 眼球を回転させる代わりに世界を逆回転させるため、符号が反転したままでOK
const float eyeRad = atan(separation / convergence);
// 視差分の移動
if (enable4d)
{
// 4D描画
const float4 eyeT = float4(-separation, 0.0f, 0.0f, 0.0f);
const float5x5 eyeTr = makeTranslation(eyeT);
const float5x5 eyeRotYW = makeRotateYW(eyeRad);
const float5x5 eyeRotYZ = makeRotateYZ(0.01 * eyeRad * squint);
const float5x5 e2 = mul5x5(eyeRotYW,eyeTr);
const float5x5 e3 = mul5x5(eyeRotYZ,e2);
return mul5x5(e3, worldView);
}
else
{
// 通常の3D描画
const float4 eyeT = float4(-separation, 0.0f, 0.0f, 0.0f);
const float5x5 eyeTr = makeTranslation(eyeT);
const float5x5 eyeRot = makeRotateYW(eyeRad);
const float5x5 e2 = mul5x5(eyeRot, eyeTr);
return mul5x5(e2, worldView);
}
}
// カメラ行列
static const float5x5 V = makeViewMatrix(
_CameraRotation1,
_CameraRotation2,
_CameraPosition,
_CameraStereoSeparation,
_CameraStereoConvergence,
_CameraSquint,
_Enable4DStereo);
頂点シェーダー本体では、上記の変換行列を使用して頂点の座標変換を行なっています。
/**
* 頂点データ構造体
*
* スクリプトで設定したvertices・colors・uvの値が設定される。
*/
struct appdata
{
float4 vertex : POSITION;
float4 color : COLOR0;
float2 uv : TEXCOORD0;
};
/**
* 頂点シェーダーからフラグメントシェーダーに渡す中間データの構造体
*
* フラグメントシェーダーでは、頂点からの距離に応じて補完された値が設定される。
*/
struct v2f
{
float4 vertex : SV_POSITION;
float4 color : COLOR0;
};
/**
* 頂点シェーダー
*
* スクリプトで設定したvertices・colors・uvの値が渡される。
* 頂点毎に呼び出される。
* 頂点を座標変換し、フラグメントシェーダーに渡す。
*/
v2f vert(appdata v)
{
v2f o;
const float5 vertex = { {v.vertex.x, v.vertex.y, v.vertex.z, v.uv.x, 1.0f} };
const float5 mv = mul5x1(M, vertex);
const float5 vmv = mul5x1(V, mv);
float4 movedVertex4 = toFloat4(vmv);
movedVertex4.w = 1.0f;
o.color = v.color;
o.vertex = mul(UNITY_MATRIX_P, movedVertex4);
return o;
}
超気持ち悪い頂点シェーダーに比べて、フラグメントシェーダーはとてもあっさりしています。
/**
* フラグメントシェーダー
*
* 頂点シェーダーの出力結果をもとに、画素毎の色の計算を行う。
* 頂点シェーダーの出力結果を画素毎に線型補完した値が渡される。
*/
float4 frag(v2f i) : SV_Target
{
// 頂点色をそのまま返す。
return i.color;
}
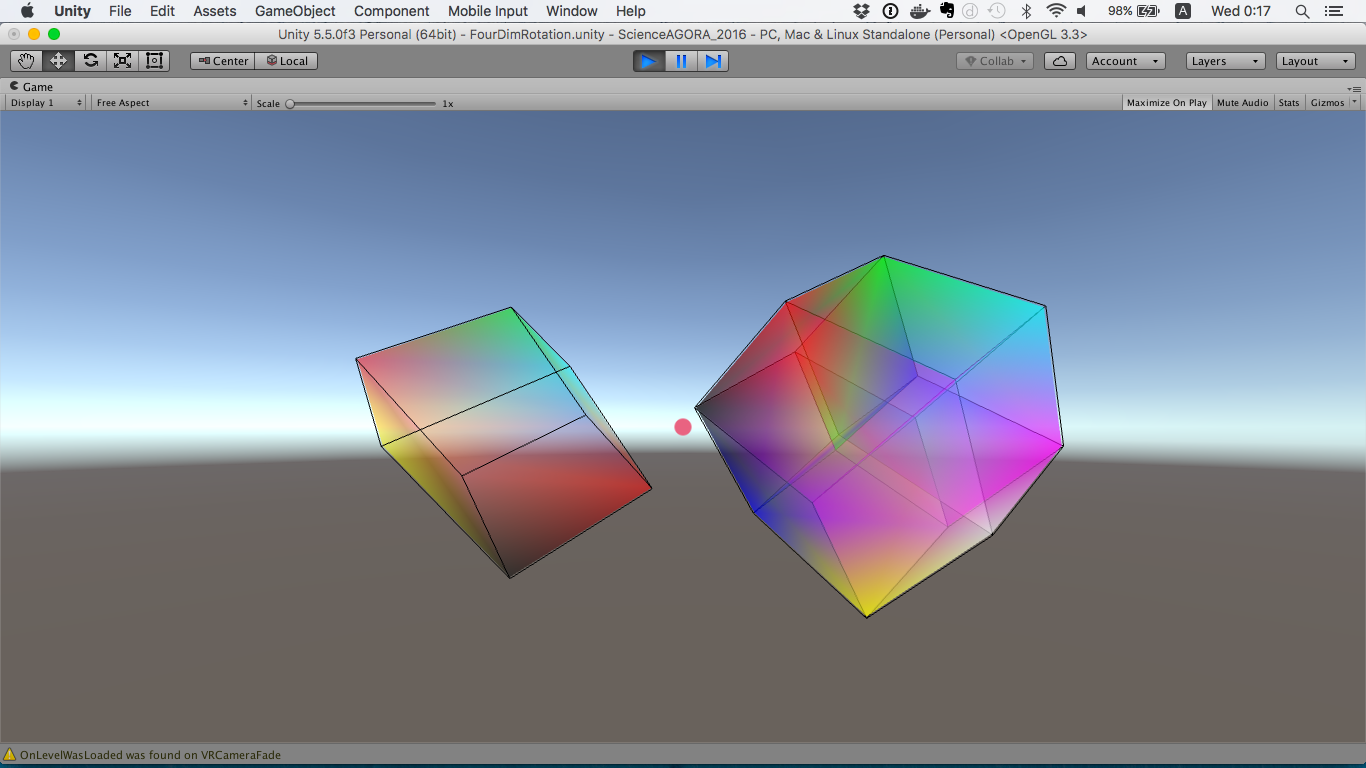
すべてを組み合わせると……。
だいたいこのような見た目になります。
詳細はかなり端折ってしまいましたが、詳細は後日コードを公開した時に見ていただけたら幸いです(汗)。
今月23日頃にOSS化の作業を行う予定で、その時にはより洗練された形で提供できると思います。
4次元に興味のある方は、上記のコンセプトを下敷きに是非実装してみてください!