Ruby-Processing ブレゼンハムのアルゴリズム

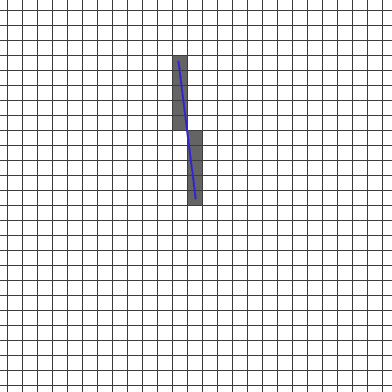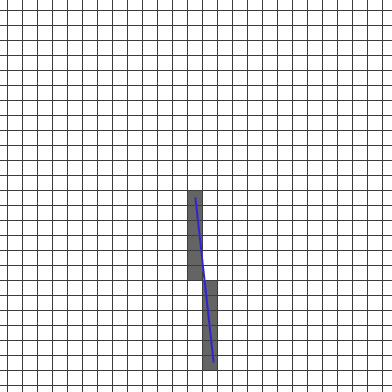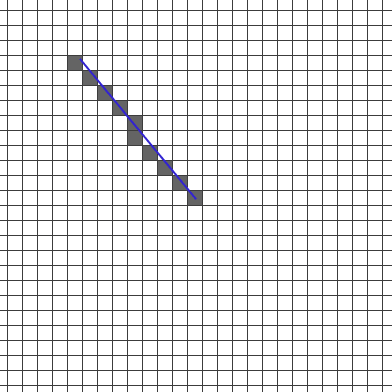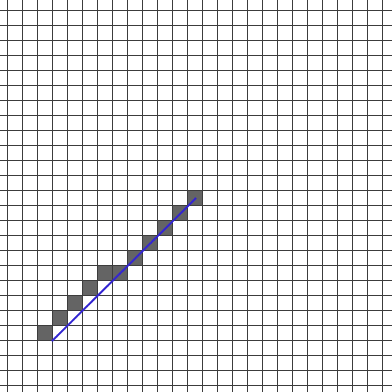
ブレゼンハムアルゴリズム を参考にさせていただいて、Ruby-Processing で実装してみました。

bresenham.rb

load_library :vecmath

# 参考
#
# プレゼンハムアルゴリズム
# http://aidiary.hatenablog.com/entry/20050402/1251514618

def setup
  size 400, 400
end

# プレゼンハムアルゴリズムを用いて
# fm から to へのラインを求める
def build_line(fm, to)
  next_x = fm.x
  next_y = fm.y
  delta_x = to.x - fm.x
  delta_y = to.y - fm.y

  step_x = delta_x < 0 ? -1 : 1
  step_y = delta_y < 0 ? -1 : 1

  delta_x = (delta_x * 2).abs
  delta_y = (delta_y * 2).abs

  line =[Vec2D.new(next_x, next_y)]

  if delta_x > delta_y
    fraction = delta_y - delta_x / 2
    while next_x != to.x
      if fraction >= 0
        next_y += step_y
        fraction -= delta_x
      end
      next_x += step_x
      fraction += delta_y
      line << Vec2D.new(next_x, next_y)
    end
  else
    fraction = delta_x - delta_y / 2
    while next_y != to.y
      if fraction >= 0
        next_x += step_x
        fraction -= delta_y
      end
      next_y += step_y
      fraction += delta_x
      line << Vec2D.new(next_x, next_y)
    end
  end
  line
end

def draw
  background 255

  translate width/2, height/2

  n = 15 # ドットひとつ分のサイズ
  rows = height / n
  cols = width / n

  rect_mode CENTER
  no_fill
  stroke 60
  for i in 0..rows
    for j in 0..cols
      rect (j-cols/2) * n, (i-rows/2) * n, n, n
    end
  end

  x = mouse_x - width/2 + n/2
  y = mouse_y - height/2 + n/2
  fm = Vec2D.new(0, 0)
  to = Vec2D.new(x / n, y / n)
  line = build_line(fm, to)
  if line
    fill(100)
    line.each {|v|
      rect v.x * n, v.y * n, n, n
    }
  end

  # マウスの位置まで line() で直線描画(ブレゼンハムアルゴリズムとの比較用)
  stroke 0x28, 0x28, 0xcc
  stroke_width 2
  line 0, 0, mouse_x - width/2, mouse_y - height/2
  stroke 0
  stroke_width 1
end

コマンドラインから次のように実行します。

$ rp5 run bresenham.rb

リンク

• Bresenham's Algorithm in JRubyArt