CourseraのMachine Learningクラス(Andrew Ng先生)のMatlab/Octaveプログラミング課題をPythonで実装するシリーズ。コンセプトは変わらず以下のとおりです:
- 課題のコードをそのまま再現するのではなく、scikit-learnなどのPythonライブラリを使ってできるだけ効率的に実装する
今週(Week6)は"Advice For Applying Machine Learning"という題で、新しい学習モデルを学ぶのではなく、モデルパラメータのチューニングの方法、モデルの性能の検証方法を学びます。このテーマに1週割り当てるあたりに、このコースの**「理論偏重ではなく実践的」**という特長が現れているのではないかと思います。
モデルのチューニング方法についての、ざくっとした内容は以下のとおり。
- データがある場合、訓練データ、交差検定(Cross-validation)データ、テストデータに分ける。Andrew先生の推奨は、6:2:2の割合。
- 訓練データを用いて、異なるモデルやパラメータで学習する。
- 交差検定をしてどのモデル・パラメータがいいか決定。その際、Learning Curveを描いて決定する。
- 最後に決定したモデルの性能をテストデータで測定する。
プログラミング課題もこの手順ですすめていきます。
まず、データの読み込み
scipyのscio.loadmat()でmatlabの.mat形式のデータを読み込めます。
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import linear_model, preprocessing
# scipy.io.loadmat()を使ってmatlabデータを読み込み
data = scio.loadmat('ex5data1.mat')
X = data['X']
Xval = data['Xval']
Xtest = data['Xtest']
y = data['y']
yval = data['yval']
ytest = data['ytest']
今回のデータは X=ダムの水位レベル を用いて、y=ダムから流出する水量 を予測するものだそうです。
まず線形回帰してみる
とりあえず線形回帰して、プロットしてみます。
model = linear_model.Ridge(alpha=0.0)
model.fit(X,y)
px = np.array(np.linspace(np.min(X),np.max(X),100)).reshape(-1,1)
py = model.predict(px)
plt.plot(px, py)
plt.scatter(X,y)
plt.show()
いつも使っているlinear_model.LinearRegression()モデルでもいいのですが、のちのち正則化項を入れるのでRidge()モデルを使っています。このモデルではパラメータのalphaで正則化の強さを指定できますが、alpha=0.0にすると正則化なしになり、LinearRegression()モデルと同じになります。
結果はこちら。
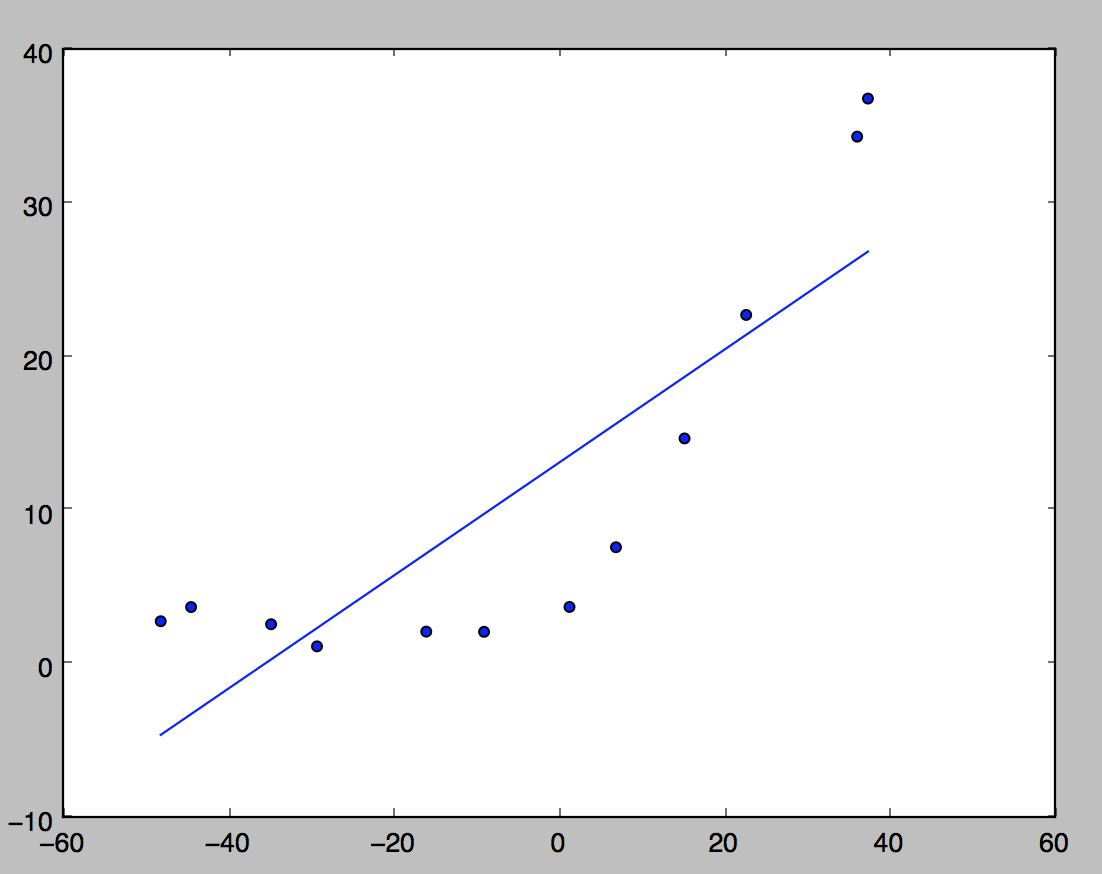
見ての通り、直線ではうまく当てはまらないデータです。
それでも線形回帰でLearning Curveを描いてみる
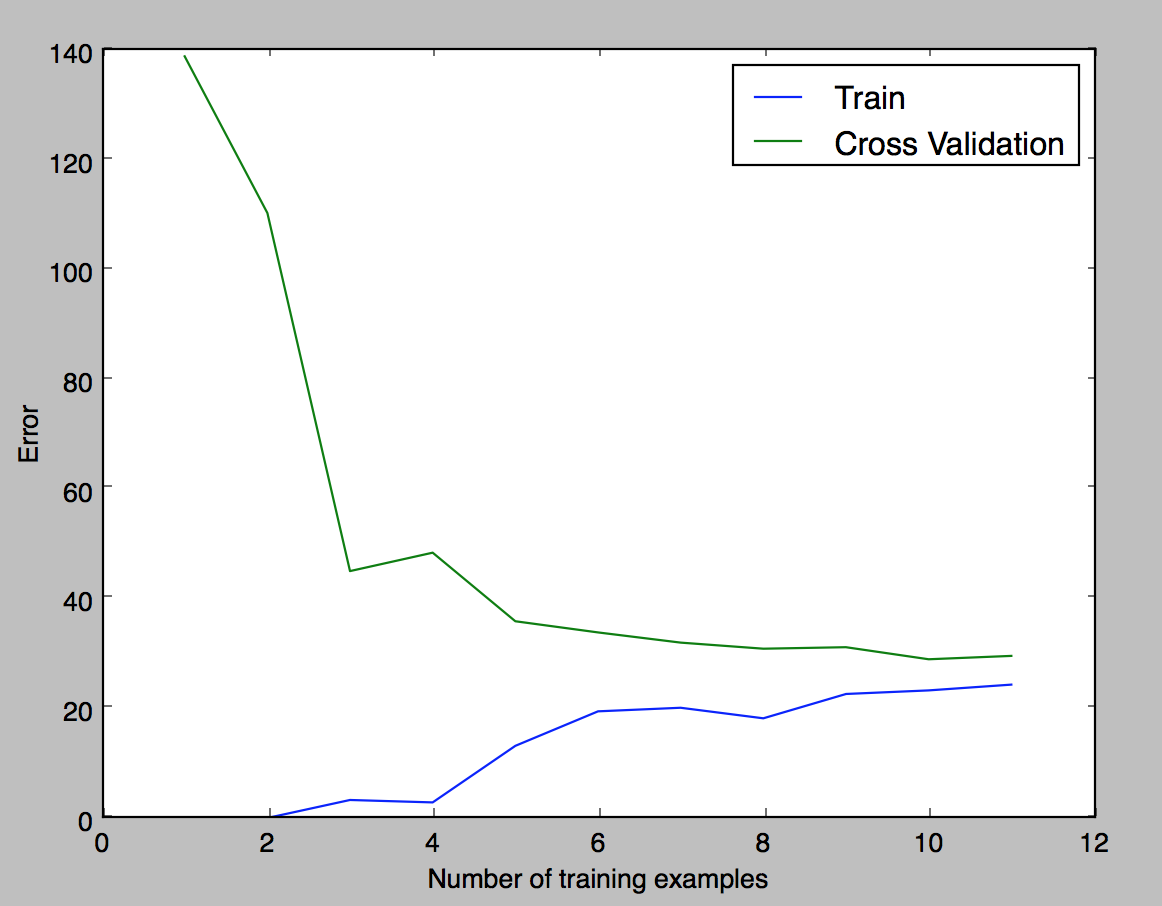
直線では当てはまらないことは知りつつも、訓練データ数を変えて学習曲線を描いてみます。訓練データを1から12個まで変えて線形回帰を行い、訓練データに対するエラーと交差検定(Cross Validation)データに対するエラーをプロットします。「エラー」は以下の式で計算できる2乗誤差です。
$$ \frac{1}{2m} \sum (h_\theta(x^{(i)}) - y^{(i)})^2 $$
コードはこちら。
# 線形回帰でLearning Curveを描いてみる
error_train = np.zeros(11)
error_val = np.zeros(11)
model = linear_model.Ridge(alpha=0.0)
for i in range(1,12):
# 訓練データのサブセットi個のみで回帰を実施
model.fit( X[0:i], y[0:i] )
# その訓練データのサブセットi個でのエラーを計算
error_train[i-1] = sum( (y[0:i] - model.predict(X[0:i]))**2 ) / (2*i)
# 交差検定用データでのエラーを計算
error_val[i-1] = sum( (yval - model.predict(Xval) )**2 ) / (2*yval.size)
px = np.arange(1,12)
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Number of training examples")
plt.ylabel("Error")
plt.legend()
plt.show()
訓練データを12(全部)まで増やしても、Trainデータ、Cross Validationデータともに誤差が下がりません。線形回帰モデルでは当てはまりが悪いということで、次は多項式フィッティングを試します。
多項式フィッティング
上で実施した線形回帰の仮説は
$$ h_\theta(x) = \theta_0 + \theta_1x$$
でしたが、多項式フィッティングはここに$x$の階乗の項を加えていきます。
$$ h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + ... + \theta_px^p$$
のような式です。
具体的には、特徴量$x$の階乗の数値をあらかじめ計算し、これを$x_1, x_2, x_3 ...$という新たな特徴量とし、このデータを用いて
$$ h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + ... + \theta_px_p$$
で表現される線形回帰モデルで学習します。
scikit-learnでは、sklearn.preprocessing.PolynomialFeaturesという、この多項式の特徴量を計算・作成してくれるクラスがあるのでこれを利用します。
コードはこちら。
# Xの階乗を計算して新しい特徴量 X_poly とする
# Xは m x 1行列、X_polyは m x 8 行列
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X)
# X_polyを使って線形回帰
model = linear_model.Ridge(alpha=0.0)
model.fit(X_poly,y)
# プロット
px = np.array(np.linspace(np.min(X)-10,np.max(X)+10,100)).reshape(-1,1)
# 今回のモデルはx_polyをインプットとして受け付けるので、プロット用のxも階乗の形に展開
px_poly = poly.fit_transform(px)
py = model.predict(px_poly)
plt.plot(px, py)
plt.scatter(X, y)
plt.show()
フィッティングの結果はこちら。
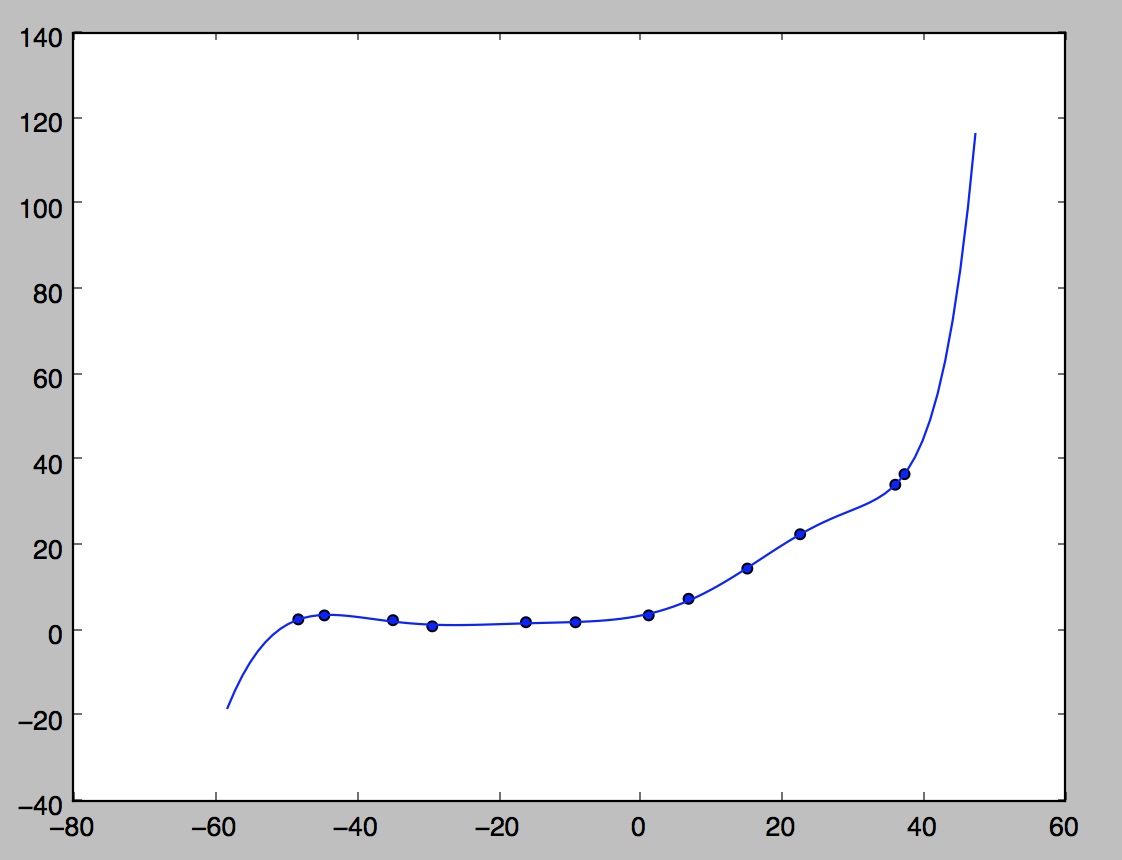
8次多項式でフィッティングするとすべての訓練データに当てはまります。が、これは過学習で、新しいデータにはうまく予測できないモデルになっている可能性があります。今度はこのモデルを交差検定用データで検証しつつ、正則化項を入れて正則化パラメータを調整していきます。
正則化パラメータのチューニング
正則化項を入れることにより、線形回帰のコスト関数は
$$ J = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2$$ のようになります。第2項が正則化項で、0から外れたパラメータの値にペナルティを与えることにより、過学習を防ぐことができます。この形の正則化をL2正則化、Ridge回帰、などと呼びます。
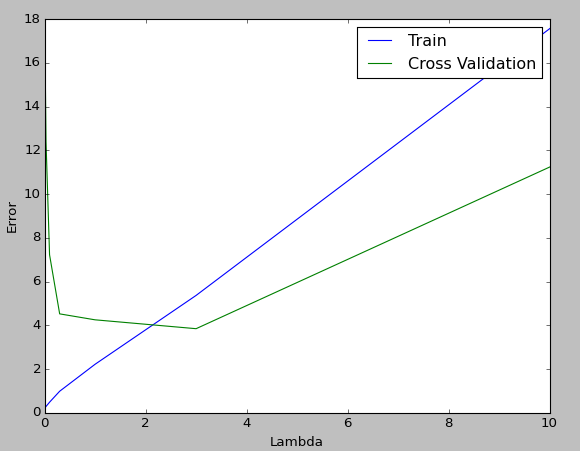
第2項の分子にある$\lambda$が正則化の強さを調整するパラメータです。上で見たように、これはlinear_model.Ridge()ではalphaパラメータに対応します。Courseraと同じくこのパラメータを 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10 と変えてlearning curveをプロットし、どの$\lambda$がいいか検討します。
コードはこちら。
# Xの階乗を計算して新しい特徴量 X_poly とする
# Xは m x 1行列、X_polyは m x 8 行列
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X) # 訓練データ
Xval_poly = poly.fit_transform(Xval) # Cross Validationデータ
# λを変えてLearning Curveを描いてみる
error_train = np.zeros(9)
error_val = np.zeros(9)
lambda_values = np.array([0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1.0, 3.0, 10.0])
for i in range(0,9):
# X_polyを使って線形回帰
model = linear_model.Ridge(alpha=lambda_values[i]/10, normalize=True ) # 正則化パラメータalphaを変える
model.fit(X_poly,y)
# 訓練データでのエラーを計算(正則化項つき)
error_train[i] = sum( (y - model.predict(X_poly))**2 ) / (2*y.size) + sum(sum( model.coef_**2 )) * lambda_values[i]/(2*y.size)
# 交差検定用データでのエラーを計算(正則化項つき)
error_val[i] = sum( (yval - model.predict(Xval_poly) )**2 ) / (2*yval.size) + sum(sum( model.coef_**2 ))* lambda_values[i]/(2*yval.size)
px = lambda_values
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Lambda")
plt.ylabel("Error")
plt.legend()
plt.show()
プロットはこのようになり、交差検定でのエラー値が最小となっている$\lambda=3$あたりがよいという結果になりました。
おわりに
sklearn.linear_model.Ridge()には交差検定用のsklearn.linear_model.RidgeCV()というモデルもあり、学習させると最適なalphaの数字をいっしょに計算してくれるようです。
参考文献