Coursera Machine Learningの課題をPythonで: ex6 (SVM パラメータの調整法)

はじめに

CourseraのMachine Learningクラス(Andrew Ng先生)の課題をPythonで実装するシリーズ。
ex6ではサポートベクターマシン(SVM)を使った分類をやります。

線形SVM

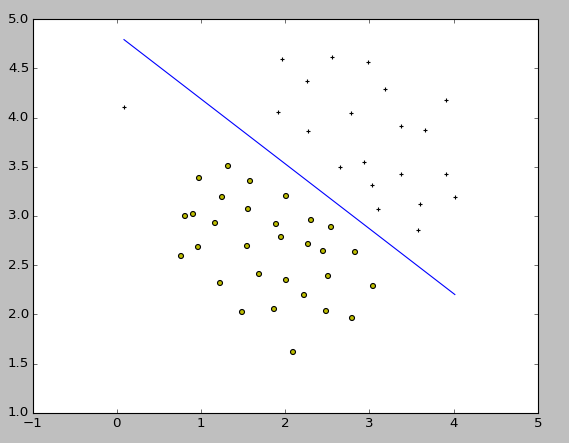
まずは線形（カーネルなし）SVMです。scikit-learnでは、機械学習のモデルのインタフェースが統一されており、どんなモデルでもインスタンスを作ってから model.fit(X,y) で学習できます。線形回帰であろうがロジスティック回帰であろうがSVMであろうが同じ文法になります。SVMはsklearn.svm.SVC()クラスを使います。

コードはこちら。
いつもと同じように、scipy.scio.loadmatを使ってMatlab形式のデータを読み込み、学習を実施します。

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm

# scipy.io.loadmat()を使ってmatlabデータを読み込み
data = scio.loadmat('ex6data1.mat')
X = data['X']
y = data['y'].ravel()

pos = (y==1) # numpy bool index
neg = (y==0) # numpy bool index
plt.scatter(X[pos,0], X[pos,1], marker='+', c='k')
plt.scatter(X[neg,0], X[neg,1], marker='o', c='y')

# 線形SVM
model = svm.SVC(C=1.0, kernel='linear')
model.fit(X, y)

# 決定境界を描く
px = np.linspace( np.min(X[:,0]), np.max(X[:,0]), 100)
w = model.coef_[0]
py = - (w[0]*px + model.intercept_[0]) / w[1]
plt.plot(px,py)
plt.show()

結果はこちら。

ここで課題に従って、SVMの正則化パラメータであるCを調整して挙動の変化を見ます。C=100.0とした結果はこちら。

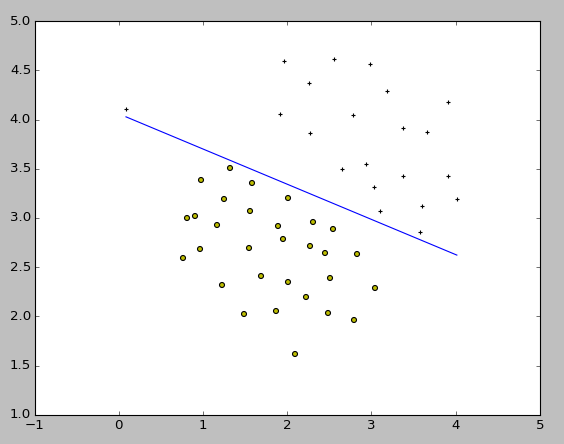
Cを大きくすると正則化が弱まります。このため、左の方にある外れ値もちゃんと分類するように決定境界が変化しています。こちらはオーバーフィット（過学習）気味で、先ほどのC=1.0とした時のほうが自然な形の分類といえるでしょう。

ガウシアンカーネルSVM

次の課題では、直線では分けるのが難しい別のデータセットをガウシアンカーネルSVMで分類します。
ガウシアンカーネルを使うので、svm.SVCのパラメータでkernel='rbf'とします。

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm

# scipy.io.loadmat()を使ってmatlabデータを読み込み
data = scio.loadmat('ex6data2.mat')
X = data['X']
y = data['y'].ravel()

pos = (y==1) # numpy bool index
neg = (y==0) # numpy bool index
plt.scatter(X[pos,0], X[pos,1], marker='+', c='k')
plt.scatter(X[neg,0], X[neg,1], marker='o', c='y')

# ガウシアンカーネル(RBF)SVM
model = svm.SVC(C=1.0, gamma=50.0, kernel='rbf', probability=True)
model.fit(X, y)

# Decision Boundary(決定境界)をプロットする
px = np.arange(0, 1, 0.01)
py = np.arange(0, 1, 0.01)
PX, PY = np.meshgrid(px, py) # PX,PYはそれぞれ 100x100 行列
XX = np.c_[PX.ravel(), PY.ravel()] # XXは 10000x2行列
Z = model.predict_proba(XX)[:,1] # SVMモデルで予測。y=1の確率は結果の2列目に入っているので取り出す。Zは10000次元ベクトル
Z = Z.reshape(PX.shape) # Zを100x100行列に変換
plt.contour(PX, PY, Z, levels=[0.5], linewidths=3) # Z=0.5の等高線が決定境界となる
plt.xlim(0.0,1.0)
plt.ylim(0.4,1.0)
plt.show()

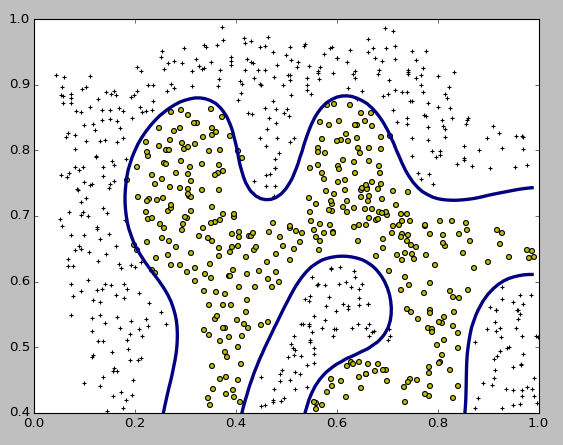
結果のプロットは以下のようになり、複雑な形の決定境界になるデータでもきれいに分類できていることがわかります。

今回ポイントになるのが、SVMのパラメータの一つであるRBFカーネルのgammaについて。Courseraでは、ガウシアンカーネルは
$$ K_{gaussian}(x^{(i)},x^{(j)}) = \exp(-\frac{||x^{(i)} - x^{(j)}||^2}{2\sigma^2}) $$
の形で定義されていました。これに対し、scikit-learnでのRBFカーネルは
$$ \exp(-\gamma \left| x-x' \right| ^2) $$
の形になっており、sklearn.svm.SVC()には$\gamma$ gammaをパラメータとして渡すようになっています。2式を見比べると、$ \gamma = \frac{1}{2\sigma^2} $ と対応しています。Courseraの例題では $\sigma = 0.1$ と設定されていたので、これに対応して $\gamma = 50$ としました。

パラメータ Cとσ の調整法

ここまでで見たように、ガウシアンカーネルSVMではパラメータCと$\sigma$の調整が必要になります。

• Cは正則化の強さ。Cが小さいほど正則化する（＝訓練データにフィットしなくなる、汎化性能が強くなる）、Cが大きいほど正則化しない（＝訓練データにフィットする、過学習になる）
• $\sigma$はガウシアンカーネルの幅の広さ。$\sigma$が大きいほど分類境界がなめらかになる

という特性を踏まえて、両方のパラメータをチューニングをしていきます。

で、次の課題では、新しいデータセットに対し、異なるCと$\sigma$の組み合わせで学習を実施し、分類の正答率が最も高いパラメータの組を採用します。Cと$\sigma$の値として 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30 の8種類の値を試すので、8x8=64回学習を実施します。
コードはこちら。

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm

# scipy.io.loadmat()を使ってmatlabデータを読み込み
data = scio.loadmat('ex6data3.mat')
X = data['X']
y = data['y'].ravel()
Xval = data['Xval']
yval = data['yval'].ravel()

c_values = np.array([0.01, 0.03, 0.1, 0.3, 1.0, 3.0, 10.0, 30.0])
gamma_values = 1/ (2* c_values**2)

# C と gamma を変えて ガウシアンカーネル(RBF)SVMを学習
scores = np.zeros([8,8])
for i_c in range(0,8):
    for i_g in range(0,8):
        model = svm.SVC(C=c_values[i_c], gamma=gamma_values[i_g], kernel='rbf')
        model.fit(X, y)
        # 交差検定用データでのスコアを算出
        scores[i_c, i_g] = model.score(Xval, yval) 

# Scoreが最大のC,gammaを求める
max_idx = np.unravel_index(np.argmax(scores), scores.shape)
# 最大のC, gammaを使って再度SVMを学習
model = svm.SVC(C=c_values[max_idx[0]], gamma=gamma_values[max_idx[1]], kernel='rbf', probability=True)
model.fit(X, y)

# 交差検定データをプロットする
pos = (yval==1) # numpy bool index
neg = (yval==0) # numpy bool index
plt.scatter(Xval[pos,0], Xval[pos,1], marker='+', c='k')
plt.scatter(Xval[neg,0], Xval[neg,1], marker='o', c='y')

# Decision Boundary(決定境界)をプロットする
px = np.arange(-0.6, 0.25, 0.01)
py = np.arange(-0.8, 0.6, 0.01)
PX, PY = np.meshgrid(px, py) # PX,PYはそれぞれ 100x100 行列
XX = np.c_[PX.ravel(), PY.ravel()] # XXは 10000x2行列
Z = model.predict_proba(XX)[:,1] # SVMモデルで予測。y=1の確率は結果の2列目に入っているので取り出す。Zは10000次元ベクトル
Z = Z.reshape(PX.shape) # Zを100x100行列に変換
plt.contour(PX, PY, Z, levels=[0.5], linewidths=3) # Z=0.5の等高線が決定境界となる
plt.show()

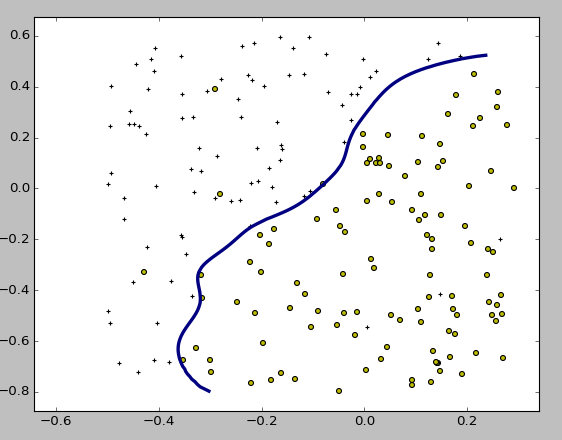
交差検定データで検証した結果 C=1.0, gamma=0.1が最も性能が高くなり、その分類器の決定境界はこのようになりました。

メモ

• numpy 2次元配列Aの中から最大値のインデックスを求める方法 --> np.unravel_index(np.argmax(A),A.shape) インデックスが入ったタプルが結果として返ってくる。

まとめ

Andrew先生は、ロジスティック回帰、線形SVM、ガウシアンカーネルSVMの使い分けについて、以下のようなガイドラインを出していました。
m= サンプル（訓練データ）数、n= featureの数とすると

• n が大きく (~10000) mが小さい (~1000) ならば、ロジスティック回帰 または 線形SVM（-->複雑な非線形決定境界をつくるほどサンプル数が多くないから）
• n が小さく (1~1000) mがほどほど (~5万)ならば ガウシアンカーネルSVM
• n が小さく (1~1000) mがとても大きい（100万とか）ならば Featureを追加して、ロジスティック回帰または線形SVM （mが大きいとガウシアンSVMは遅いから）

ex6の後半（SVMを用いたスパムフィルター）は別途やります。