この文章は書籍『アルゴリズムパズル』の問37の解答を作るために書いたノートの一部です。
整数$n > 1$は、2以上の偶数または奇数である。nが偶数、奇数のいずれの場合にも条件を満たす貨幣の配位を作り出す方法を示せば、それが問題の解答になる。
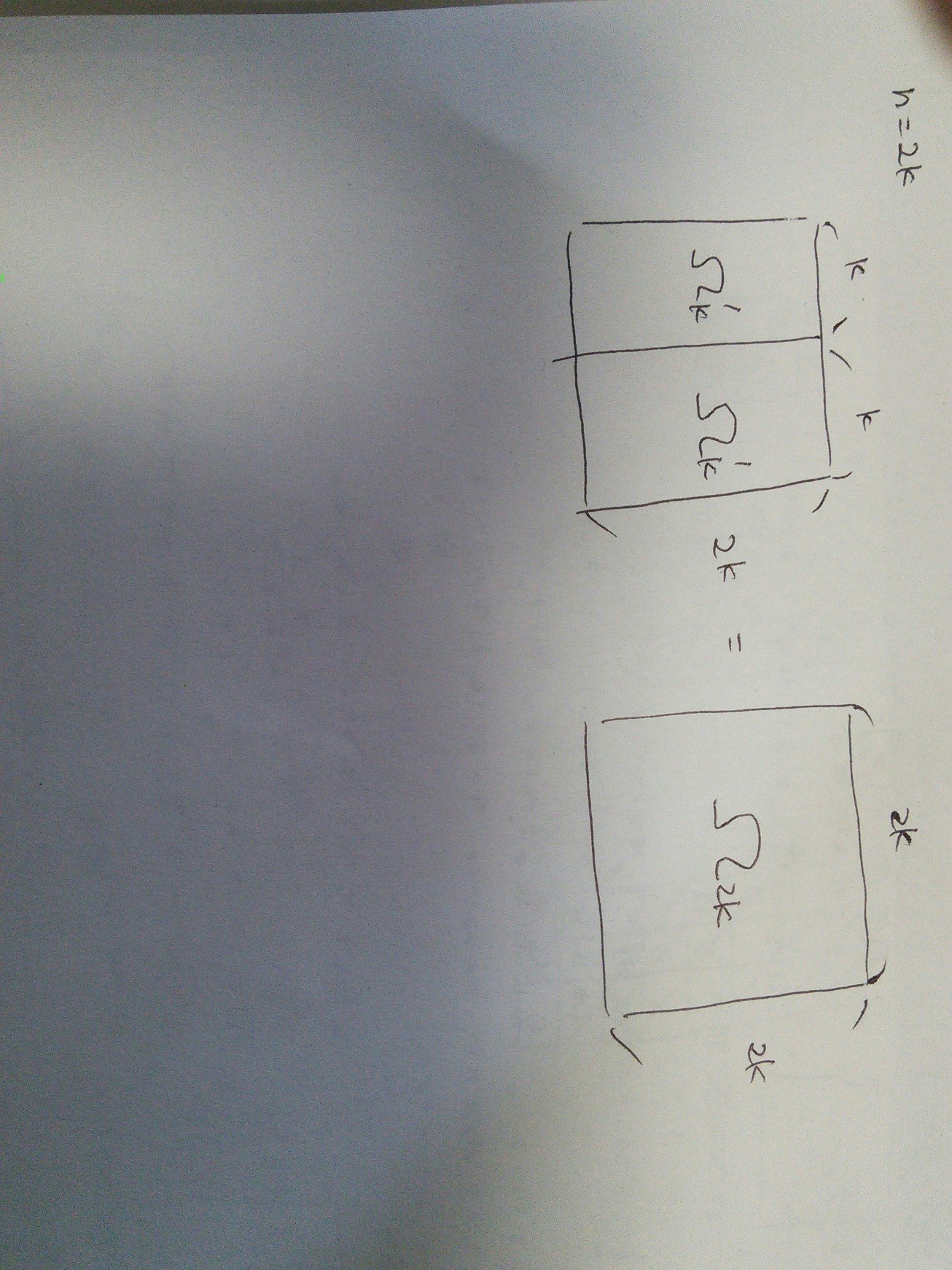
まずは2以上の偶数の場合の貨幣の配位の作り方を考える。$n$を1以上の整数$k$を使って$n=2k$であらわし、このときの貨幣の配位を$\Omega_{2k}$と書くことにする。
$\Omega_{2k}$は、上の図のように$\Omega_{k}^{\prime}$を2つ並べることで作ることができる。$\Omega_{k}^{\prime}$は$2k\times k$の盤面に同じ列、斜めには2以下の貨幣、同じ行には1つ以下の貨幣を合計2k個置いた配位である。ただし、斜めの効果が横に並んだ配位に互いに影響を与えるので、このままでは互いに独立に考えることができない。そこで、左右のマスについては、右と左が繋がっていると考えた上で、上のように書いた配位が作れるかを考える。すると、左と右の配位は完全に別々に考えることができるようになる。
任意の$k$について$\Omega_{k}^{\prime}$の作り方を見つけられれば良いのだけれども、今のところ、うまい方法が思いつかない。更に問題を簡単にするために、斜めの制限をはずして、次回考えてみる。