複数の画像を組み合わせて1枚の画像を作る,コラージュというものがある.
ほとんどのコラージュサービスは,コラージュテンプレートに画像を埋め込むことでこれを実現する.
今回はこのコラージュテンプレートを確率的に生成してみようと思う.
これは,1つの長方形を$n$個の長方形に分割することで実現できる.
この手順を確率的に表現して,乱数のseedを変えることでテンプレートを無限に生成できるようにする.与えるのは$n$のみである.
1ステップで領域を1つ分割するとする.
選ばれる領域は,カテゴリ分布に従うとする.一様分布でも良いが,領域が大きいところを優先的に分割したいみたいな場合を想定して多項分布にしている(今回のコードでは一様分布と同じ).最初は1つの領域しかないので,これが選ばれる.次は2つあるのでどちらかを選び分割する.次は3つあるので...といった具合だ.
さて,分割する領域を決定したあとはこれをどう分割するかを決める.
分割というのは,直線(4次元以上だと超平面)を一つ定めることに対応する.
つまり,直線$w^T x - b$の,$w$と$b$を定めれば良い.
なお,今回は斜めの分割はしないことにする.
そうすると,分割の仕方は縦方向と横方向の2つしかない.
つまり,$w = [1 \ 0]^T$または,$w = [0 \ 1]^T$のみである.
今回は,分割の仕方はベルヌーイ分布に従うとする.
こうすると,残るはbを決めるだけだ.これは一様分布に従うとする.
$b = [b_1 \ b_2]$として,$b \sim U(0, w)$,$b \sim U(0, h)$とする.
ただし,$w$は分割する領域の横幅で,$h$は分割する領域の縦幅である.
ここは真ん中らへんが優先的に分割されるよう,正規分布とかにしても良いかもしれない.
以上で手順は終了.実験してみた.コードは最後に添付する.
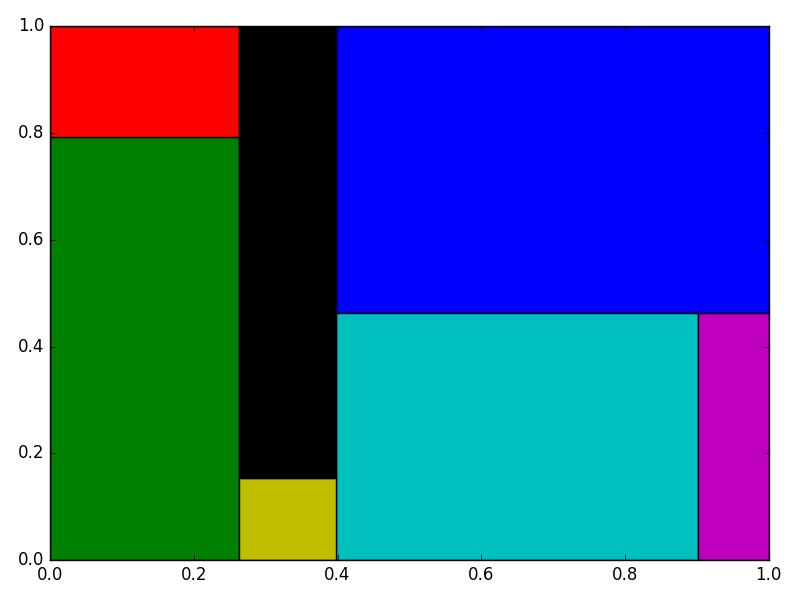
$n = 7$の例を示して終わりにする.
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
def generate_template(n, width, height, random_state=1, max_random_state=10000, offset=0):
L = [np.array([offset, offset, width-offset, height-offset])]
random_state_lists = stats.randint.rvs(0, max_random_state, size=(n-1, 4), random_state=random_state)
for random_state_list in random_state_lists:
n_areas = len(L)
if n_areas == 1:
i = 0
else:
p = np.repeat(1 / (n_areas + i), n_areas)
x = stats.multinomial.rvs(1, p, size=1, random_state=random_state_list[0])[0]
i = x.argmax()
y = stats.bernoulli.rvs(0.5, size=1, random_state=random_state_list[1])[0]
if y == 0:
b = stats.uniform.rvs(L[i][0], L[i][2] - L[i][0], size=1, random_state=random_state_list[2])[0]
#b = stats.uniform.rvs(L[i][0], L[i][2] - L[i][0], size=1, random_state=random_state_list[2])[0]
else:
b = stats.uniform.rvs(L[i][1], L[i][3] - L[i][1], size=1, random_state=random_state_list[3])[0]
#b = stats.uniform.rvs(L[i][1], L[i][3] - L[i][1], size=1, random_state=random_state_list[3])[0]
if y == 0:
area1 = np.array([L[i][0], L[i][1], b-offset/2, L[i][3]])
area2 = np.array([b+offset/2, L[i][1], L[i][2], L[i][3]])
else:
area1 = np.array([L[i][0], L[i][1], L[i][2], b-offset/2])
area2 = np.array([L[i][0], b+offset/2, L[i][2], L[i][3]])
L.pop(i)
L.append(area1)
L.append(area2)
return L
L = generate_template(7, 1, 1, random_state=3, offset=0)
colors=["b", "g", "r", "c", "m", "y", "k"]
fig = plt.figure()
ax = fig.add_subplot(111)
for l_i, c_i in zip(L, colors):
rect = plt.Rectangle(xy=[l_i[0], l_i[1]], width=l_i[2] - l_i[0], height=l_i[3] - l_i[1], facecolor=c_i, fill=True)
ax.add_patch(rect)
plt.tight_layout()
plt.show()