2点間の距離計算 (C, Clojure, Go, Haskell, Java, LOGO, OCaml, Ruby, Rust, Scratch, Swift)

地球を真球とみなして、緯度経度による2点間の距離をいろいろなプログラミング言語で計算する。

基本方針は以下。

• 関数/メソッド1つをコピペして使えそうなコードにする
• require/import系を書かなくてよいなら書かない
• 標準ライブラリだけを使う
• 関数/メソッドの引数はプリミティブな浮動小数点4つ
• 変数/再代入不可変数/定数については「シンプルで違和感のない表現で」と思ってはいるけど決めかねている

C

#include <math.h>
#include <stdio.h>

// 球面三角法により、大円距離(メートル)を求める
double distance(double lat1, double lng1, double lat2, double lng2) {

    // 円周率
    const double pi = 3.14159265359;

    // 緯度経度をラジアンに変換
    double rlat1 = lat1 * pi / 180;
    double rlng1 = lng1 * pi / 180;
    double rlat2 = lat2 * pi / 180;
    double rlng2 = lng2 * pi / 180;

    // 2点の中心角(ラジアン)を求める
    double a =
      sin(rlat1) * sin(rlat2) +
      cos(rlat1) * cos(rlat2) *
      cos(rlng1 - rlng2);
    double rr = acos(a);

    // 地球赤道半径(メートル)
    const double earth_radius = 6378140;

    // 2点間の距離(メートル)
    double distance = earth_radius * rr;

    return distance;
}

int main(int argc, char *argv[]) {
  // 計算サンプル
  printf("%f\n", distance(35.1730990, 136.883466, 35.1855732, 136.899092));
  printf("%f\n", distance(35.1855732, 136.899092, 35.1730990, 136.883466));
  return 0;
}

Clojure

; 球面三角法により、大円距離(メートル)を求める
(defn distance [lat1 lng1 lat2 lng2]

  ; 緯度経度をラジアンに変換
  (let [rlat1 (/ (* lat1 Math/PI) 180)
        rlng1 (/ (* lng1 Math/PI) 180)
        rlat2 (/ (* lat2 Math/PI) 180)
        rlng2 (/ (* lng2 Math/PI) 180)

        ; 2点の中心角(ラジアン)を求める
        a (+ (* (Math/sin rlat1) (Math/sin rlat2))
             (* (* (Math/cos rlat1) (Math/cos rlat2))
                (Math/cos (- rlng1 rlng2))))
        rr (Math/acos a)

        ; 地球赤道半径(メートル)
        earth_radius 6378140]

  ; 2点間の距離(メートル)
  (* earth_radius rr)))

; 計算サンプル
(println (distance 35.1730990 136.883466 35.1855732 136.899092))
(println (distance 35.1855732 136.899092 35.1730990 136.883466))

Go

package main

import (
  "fmt"
  "math"
)

func main() {
  // 計算サンプル
  fmt.Printf("%f\n", distance(35.1730990, 136.883466, 35.1855732, 136.899092));
  fmt.Printf("%f\n", distance(35.1855732, 136.899092, 35.1730990, 136.883466));
}

// 球面三角法により、大円距離(メートル)を求める
func distance(lat1 float64, lng1 float64, lat2 float64, lng2 float64) float64 {

  // 緯度経度をラジアンに変換
  rlat1 := lat1 * math.Pi / 180
  rlng1 := lng1 * math.Pi / 180
  rlat2 := lat2 * math.Pi / 180
  rlng2 := lng2 * math.Pi / 180

  // 2点の中心角(ラジアン)を求める
  a :=
    math.Sin(rlat1) * math.Sin(rlat2) +
    math.Cos(rlat1) * math.Cos(rlat2) *
    math.Cos(rlng1 - rlng2)
  rr := math.Acos(a)

  earth_radius := 6378140. // 地球赤道半径(メートル)
  distance := earth_radius * rr
  return distance
}

Haskell

-- 球面三角法により、大円距離(メートル)を求める
distance :: Double -> Double -> Double -> Double -> Double
distance lat1 lng1 lat2 lng2 = let {

  -- 緯度経度をラジアンに変換
  rlat1 = lat1 * pi / 180;
  rlng1 = lng1 * pi / 180;
  rlat2 = lat2 * pi / 180;
  rlng2 = lng2 * pi / 180;

  -- 2点の中心角(ラジアン)を求める
  a = sin rlat1 * sin rlat2 + cos rlat1 * cos rlat2 * cos (rlng1 - rlng2);
  rr = acos a;

  earth_radius = 6378140; -- 地球赤道半径(メートル)
  distance = earth_radius * rr;

} in distance

main = do
  -- 計算サンプル
  print (distance 35.1730990 136.883466 35.1855732 136.899092)
  print (distance 35.1855732 136.899092 35.1730990 136.883466)

Java

public class Earth {

  public static void main(String args[]) {
    // 計算サンプル
    System.out.println(distance(35.1730990, 136.883466, 35.1855732, 136.899092));
    System.out.println(distance(35.1855732, 136.899092, 35.1730990, 136.883466));
  }

  // 球面三角法により、大円距離(メートル)を求める
  public static double distance(double lat1, double lng1, double lat2, double lng2) {

    // 緯度経度をラジアンに変換
    double rlat1 = Math.toRadians(lat1);
    double rlng1 = Math.toRadians(lng1);
    double rlat2 = Math.toRadians(lat2);
    double rlng2 = Math.toRadians(lng2);

    // 2点の中心角(ラジアン)を求める
    double a =
      Math.sin(rlat1) * Math.sin(rlat2) +
      Math.cos(rlat1) * Math.cos(rlat2) *
      Math.cos(rlng1 - rlng2);
    double rr = Math.acos(a);

    // 地球赤道半径(メートル)
    double earth_radius = 6378140;

    // 2点間の距離(メートル)
    double distance = earth_radius * rr;

    return distance;
  }
}

LOGO

; 球面三角法により、大円距離(メートル)を求める
to distance :lat1 :lng1 :lat2 :lng2

  ; 円周率
  make "pi (radarctan 0 1) * 2

  ; 緯度経度をラジアンに変換
  make "rlat1 :lat1 * :pi / 180
  make "rlng1 :lng1 * :pi / 180
  make "rlat2 :lat2 * :pi / 180
  make "rlng2 :lng2 * :pi / 180

  ; 2点の中心角(ラジアン)を求める
  make "a1 (radsin :rlat1) * (radsin :rlat2)
  make "a2 (radcos :rlat1) * (radcos :rlat2)
  make "a3 radcos (rlng1 - rlng2)
  make "a :a1 + :a2 * :a3
  make "b sqrt((-1 * :a * :a) + 1)
  make "c radarctan((-1 * :a) / :b)
  make "rr :c + :pi / 2

  ; 地球赤道半径(メートル)
  make "earth_radius 6378140

  ; 2点間の距離(メートル)
  make "distance :earth_radius * :rr

  output :distance
end

; 計算サンプル
print distance 35.1730990 136.883466 35.1855732 136.899092
print distance 35.1855732 136.899092 35.1730990 136.883466

OCaml

(* 球面三角法により、大円距離(メートル)を求める *)
let distance lat1 lng1 lat2 lng2 =

  (* 円周率 *)
  let pi = 3.14159265359 in

  (* 緯度経度をラジアンに変換 *)
  let rlat1 = lat1 *. pi /. 180. in
  let rlng1 = lng1 *. pi /. 180. in
  let rlat2 = lat2 *. pi /. 180. in
  let rlng2 = lng2 *. pi /. 180. in

  (* 2点の中心角(ラジアン)を求める *)
  let a = sin rlat1 *. sin rlat2 +. cos rlat1 *. cos rlat2 *. cos (rlng1 -. rlng2) in
  let rr = acos a in

  let earth_radius = 6378140. in (* 地球赤道半径(メートル) *)
  let distance = earth_radius *. rr in

  distance;;

(* 計算サンプル *)
print_endline (string_of_float (distance 35.1730990 136.883466 35.1855732 136.899092));;
print_endline (string_of_float (distance 35.1855732 136.899092 35.1730990 136.883466));;

Ruby

# 球面三角法により、大円距離(メートル)を求める
def distance(lat1, lng1, lat2, lng2)

  # 緯度経度をラジアンに変換
  rlat1 = lat1 * Math::PI / 180
  rlng1 = lng1 * Math::PI / 180
  rlat2 = lat2 * Math::PI / 180
  rlng2 = lng2 * Math::PI / 180

  # 2点の中心角(ラジアン)を求める
  a =
    Math::sin(rlat1) * Math::sin(rlat2) +
    Math::cos(rlat1) * Math::cos(rlat2) *
    Math::cos(rlng1 - rlng2)
  rr = Math::acos(a)

  earth_radius = 6378140 # 地球赤道半径(メートル)
  earth_radius * rr
end

# 計算サンプル
puts distance(35.1730990, 136.883466, 35.1855732, 136.899092)
puts distance(35.1855732, 136.899092, 35.1730990, 136.883466)

Rust

fn main() {
  // 計算サンプル
  println!("{}", distance(35.1730990, 136.883466, 35.1855732, 136.899092));
  println!("{}", distance(35.1855732, 136.899092, 35.1730990, 136.883466));
}

// 球面三角法により、大円距離(メートル)を求める
fn distance(lat1: f64, lng1: f64, lat2: f64, lng2: f64) -> f64 {

  // 緯度経度をラジアンに変換
  let rlat1 = lat1.to_radians();
  let rlng1 = lng1.to_radians();
  let rlat2 = lat2.to_radians();
  let rlng2 = lng2.to_radians();

  // 2点の中心角(ラジアン)を求める
  let a =
    rlat1.sin() * rlat2.sin() +
    rlat1.cos() * rlat2.cos() *
    (rlng1 - rlng2).cos();
  let rr = a.acos();

  let earth_radius = 6378140.; // 地球赤道半径(メートル)
  earth_radius * rr
}

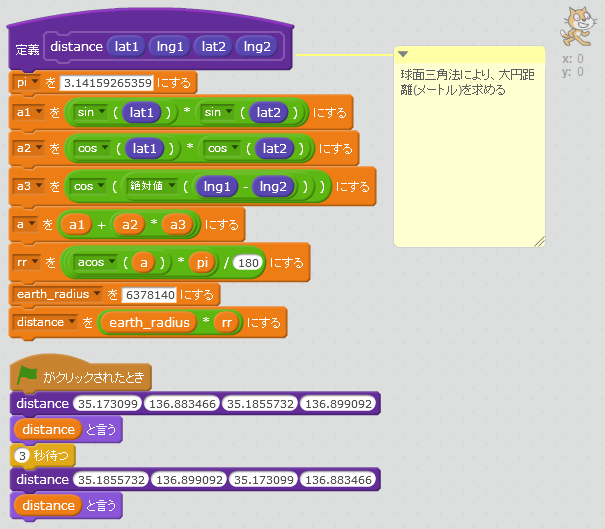
Scratch

Swift

import Foundation

// 球面三角法により、大円距離(メートル)を求める
func distance(lat1: Double, lng1: Double, lat2: Double, lng2: Double) -> Double {
    
  // 緯度経度をラジアンに変換
  let rlat1 = lat1 * M_PI / 180
  let rlng1 = lng1 * M_PI / 180
  let rlat2 = lat2 * M_PI / 180
  let rlng2 = lng2 * M_PI / 180
    
  // 2点の中心角(ラジアン)を求める
  let a =
    sin(rlat1) * sin(rlat2) +
    cos(rlat1) * cos(rlat2) *
    cos(rlng1 - rlng2)
  let rr = acos(a)
    
  // 地球赤道半径(メートル)
  let earth_radius = 6378140.0
    
  // 2点間の距離(メートル)
  let distance = earth_radius * rr
    
  return distance
}

// 計算サンプル
print("\(distance(lat1: 35.1730990, lng1: 136.883466, lat2: 35.1855732, lng2: 136.899092))")
print("\(distance(lat1: 35.1855732, lng1: 136.899092, lat2: 35.1730990, lng2: 136.883466))")

参考資料

• 大円距離 - Wikipedia https://ja.wikipedia.org/wiki/%E5%A4%A7%E5%86%86%E8%B7%9D%E9%9B%A2