みどり本の図10.4をStanで描画方法と信頼区間・予測区間

はじめ

図10.4「生存種子数yの予測分布をstanで作成する」以降の予測区間の説明内容に誤りがあります、現在見直し中

自習用にstanを使い「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル・MCMC)」の「10.3.3 階層ベイズモデルの事後分布推測と予測」の信頼区間と予測区間の求め方をまとめました

上記の章に出てくる図10.4「生存種子数yの予測分布$p(Y|β,s)$と観測データ」をstanで求める方法を初心者がまとめたものです

時間がある方は、このまとめより"StanとRでベイズ統計モデリング"を読むことを強くお勧めします

http://www.kyoritsu-pub.co.jp/bookdetail/9784320112421

用語の確認

Stan

マルコフ連鎖モンテカルロ法(MCMC)を用いた統計モデリング言語です

• C++で実装
• RとPythonのインターフェースがある

統計モデリング

数理モデルを作って観測データをあてはめて現象を解釈、予測することです

あてはめ

あてはめとは、数理モデルに含まれるパラメータを観測データから推測することです
あてはめの方法に、ベイズ推定と最尤推定があります

解釈と予測

統計モデリングの目的は、現象を解釈または現象を予測することです
解釈は、その現象が発生する仕組みを知るためです
予測は、いままで得られたデータから未来（または過去）を予測することです

解釈、予測の結果を評価する方法の１つに区間推定があります
解釈に対応する区間推定が信頼区間、予測に対応するのが予測区間です

-	区間推定	式	範囲
解釈	信頼区間	$p(\theta|Y)$	予測区間より範囲は狭い
予測	予測区間	$p(y|Y)$	信頼区間より範囲は広い

Y:観測データ
$\theta$:パラメータ
y:予測データ

StanとRでベイズ統計モデリング　の図4-8 年齢から年収推測するもでるの左が信頼区間、右が予測区間

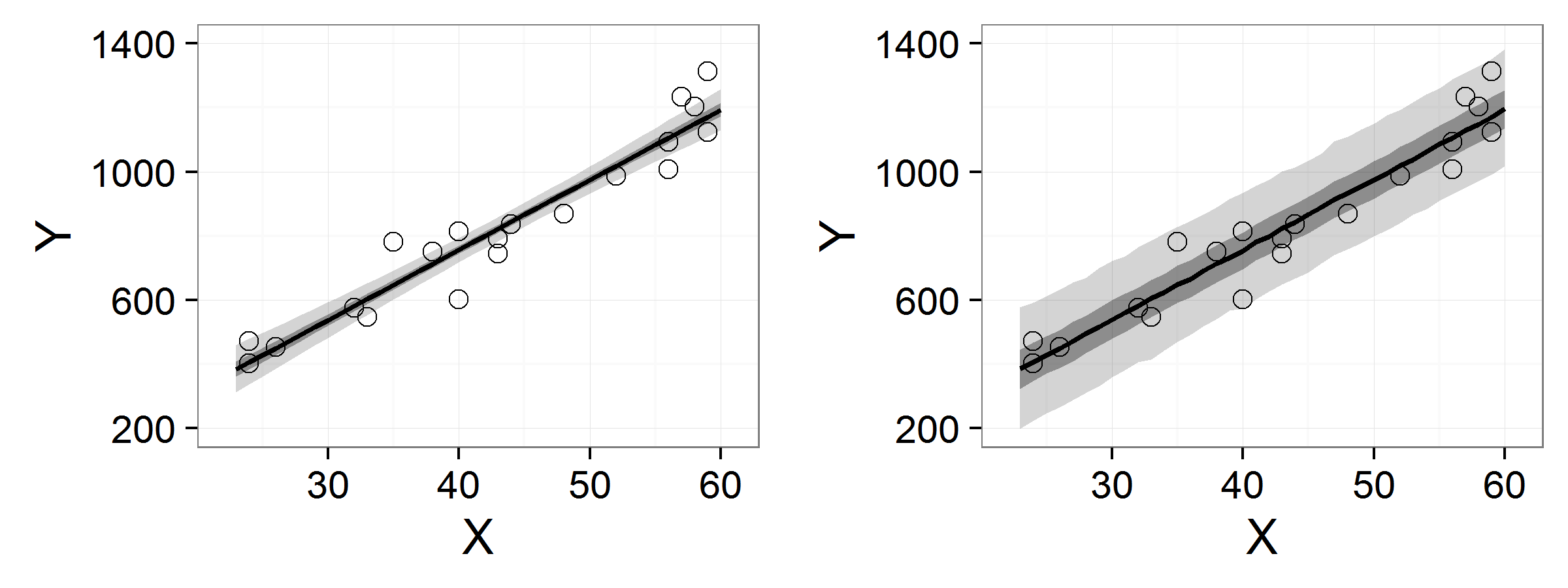
ベイズ統計モデリング

ベイズ定理を利用して統計モデリングを行うことです
あてはめや解釈と予測にベイズ推定を利用します

信頼区間

観測データであてはめたパラメータが、区間内にある確率、または当たっている確率です
95%信頼区間の場合2.5％点から97.5％点の区間内にある確率、または当たっている確率です

StanとRでベイズ統計モデリング　の図4-8 年齢から年収推測の50%と95%信頼区間

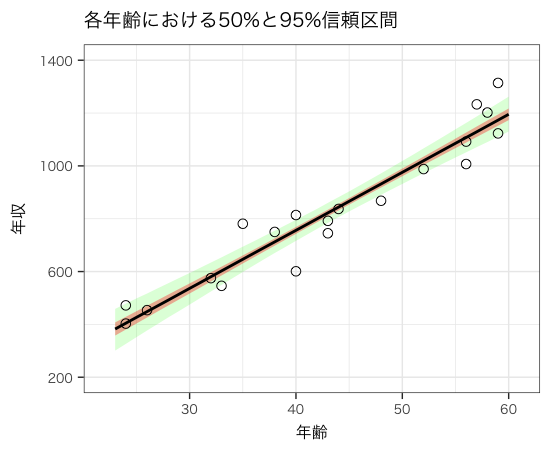
あてはめ方法と信頼区間の解釈
信頼区間の解釈は統計モデリングの手法に依存します

手法	あてはめ方法	信頼区間の解釈	解釈のしやすさ
古典的統計モデリング	最尤推定	100回データをとりなおして解析した場合、区間内に95回くらいはいる	×
ベイズ統計モデリング	ベイズ推定	パラメータが区間内にある確率は95% 信用区間ともいう	◯

予測と予測区間

予測区間は観察されるであろう標本値（現在は測定できない）に対して「どの範囲にあると予測されるか」を示しています

StanとRでベイズ統計モデリング　の図4-8 年齢から年収推測の50%と95%予測区間

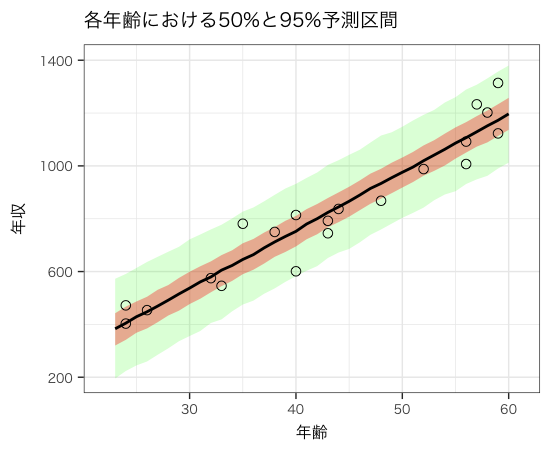
信頼区間と予測区間の数式

例題:個体差と生存種子数(個体差あり）

「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル・MCMC)」の例題
ある植物から種子を8個とり、生存種子が何個あるかを観測したデータがあります

id	y(生存種子数)
1	0
2	2
3	7
...	...
100	1

属性	値
調査した種子数	100
調査種子数	8
求めるもの	生存種子の数
モデル	ベイズ階層モデル
分布	二項分布と正規分布の混合分布

信頼区間の求め方

ベイズ推定の信頼区間は事後分布と一致します

事後分布の計算式

事後分布 = \frac{尤度×事前分布}{データが得られる確率} \propto 尤度×事前分布

属性	式
事後分布	$p(\theta|Y) $
尤度	$p(Y|\theta)$
事前分布	$p(\theta)$
データが得られる確率	p(Y)

 p(θ|Y) =  \frac{p(Y|\theta)p(\theta)}{p(Y)} \propto p(y|\theta)p(\theta)

例題の場合

階層ベイズモデル

パラメータ	説明
β	切片
{r}	個体差
s	個体差を生み出す標準偏差

p(β,{r},s|Y) \propto  p(y|β,{r},s)p(β,{r},s)

予測の求め方

得られたパラメータの事後分布で重み付けし、確率モデルを足し合わせます

予測の数式

属性	式
事後分布	$p(\theta|Y) $
確率モデル	$p(y|\theta)$

p_{{pred}}(y|Y) = \int p(y|\theta)p(\theta|Y)d\theta

Stanで信頼区間を求める

MCMC結果の事後分布から分位点を算出するだけ！
95%信頼区間なら、0.025分位点から0.975分位点をみるだけです

Stanで予測を求める

予測区間の求め方を二つ解説します

• パラメータを積分して求める方法
• MCMCサンプルのパラメータから乱数を作り、乱数の分布を予測分布とする

予測分布の作成方法	あてはめ	予測	特徴
パラメータを積分して周辺化	Stan	R	パラメータが複雑だと積分が大変
パラメータから乱数を作り、新たな分布を作成	Stan	Stan	あてはめと同時に予測もできる

あてはめ、予測のStan,Rの選択はこのまとめでの実現方法です

例題でのStanモデルファイル

StanとRでベイズ統計モデリングのサポートページのモデルのgenerated quantities部分を加えました
https://github.com/MatsuuraKentaro/RStanBook

ex6.stan

data {
  int N;//調査した種子数 
  int Y[N];//生存種子数
}

parameters {
  real b;//切片　
  real b_I[N];//個体差
  real<lower=0> s_I;//個体差を生み出す標準偏差
}

transformed parameters {
  real q[N];
  for (n in 1:N)
    q[n] = inv_logit(b + b_I[n]);
}

model {
  for (n in 1:N)
    b_I[n] ~ normal(0, s_I);

  for (n in 1:N)
    Y[n] ~ binomial(8, q[n]);
}
generated quantities {
  real b_I_new;//切片の予測分布
  real q_new;//個体差を生み出す標準偏差の予測分布
  real y_pred;//生存種子数の予測分布
  
  for (i in 1:4000){
#予測区間を作るだけならループは不要
#図10.4と同じ図をstanだけで作るときにループが必要
      b_I_new = normal_rng(0, s_I);  
      q_new =inv_logit(b + b_I_new);
　    y_pred[i] = binomial_rng(8,q_new);
  }
}

パラメータを積分して周辺化

p_{{pred}}(y|β,s) = \int p(y|β,r)p(r|s)dr

パラメータのうち個体差である$r$を積分し、rが取りうる全ての値をとる分布を作成する

予測分布に対応する分位点が予測区間となる

「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル)」図 10.4: fig10_04.RをWinBugsからstanに改変し、必要な部分のみ抽出したソースです。
（全ソースは最後にあります）
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html

fig10_04_to_Stan.R

library(rstan)
#install.packages("gtools")
library(gtools)

d <- read.csv('http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/data7a.csv')
N <- nrow(d)
data <- list(N=N, Y=d$y)
##################################
###Stanでサンプリング
fit <- stan(file='ex6.stan', data=data, seed=1234)
ms <- rstan::extract(fit)
#積分する関数の定義
f.gaussian.binom <- function(alpha, x, size, fixed, sd)
  dbinom(x, size, logistic(fixed + alpha)) * dnorm(alpha, 0, sd)

#積分の呼び出し
d.gaussian.binom <- function(v.x, size, fixed, sd) sapply(
  #積分
  v.x, function(x) integrate(
    f = f.gaussian.binom,
    lower = -sd * 10,
    upper = sd * 10,
    # for f.gaussian.binom
    x = x,
    size = size,
    fixed = fixed,
    sd = sd
  )$value
)
#Stanの結果代入
beta <- ms$b
sigma <- ms$s_I


cat("# generating mp（事後確率推定値 ")
mp <- sapply(
  1:3,#MCMCのサンプルから3件のみ抽出
  function(i) {
    if (i %% 100 == 0) cat(".")
    d.gaussian.binom(
      0:size, size,
      fixed = beta[i],
      sd = sigma[i]
    )
  }
)

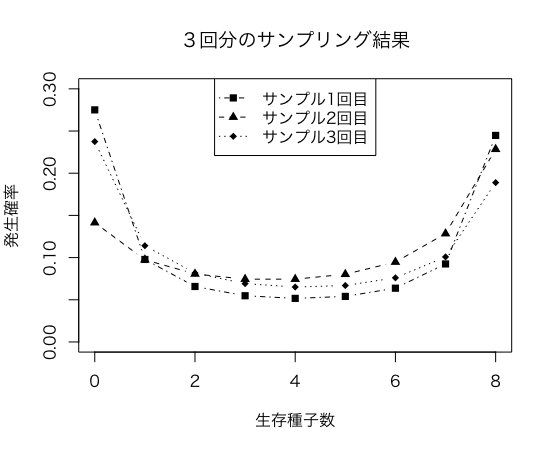
実行結果

サンプルとして3件のみ抽出した結果です
生存種子数ごとの発生確率となります

生存種子数(個）	1回目	2回目	3回目
0	0.27507605	0.14140127	0.23749017
1	0.09778946	0.09744419	0.11407421
2	0.06574734	0.08061195	0.08159960
3	0.05477573	0.07441558	0.06915147
4	0.05164282	0.07442238	0.06508034
5	0.05399055	0.08024038	0.06690871
6	0.06372340	0.09468573	0.07601883
7	0.09246606	0.12840177	0.10080378
8	0.24478855	0.22837675	0.18887288

パラメータから乱数を作り、新たな分布を作成

stanだけで実現できます
具体的には「model」パラグラフまたは「generated quantities」パラグラフ部分で記載します
今回は「generated quantities」で予測してみました

「generated quantities」で定義した、予測結果のy_predを分布としています。
「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル)」図 10.4のようなグラフを書くには、generated quantitiesで4000回ほどのループすればよさそうです。

fig10_04_to_Stan.R

library(rstan)
#install.packages("gtools")
library(gtools)

d <- read.csv('http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/data7a.csv')
N <- nrow(d)
data <- list(N=N, Y=d$y)
##################################
###Stanでサンプリング
fit <- stan(file='ex6.stan', data=data, seed=1234)
ms <- rstan::extract(fit)

plot(
  0:size, 
  table(ms$y_pred[1,]),type = "b",
  ylim = range(c(0, 1300)),#
  xlab = "生存種子数",
  ylab = "サンプリング時の頻度",
  pch = 0, main="３回分のサンプリング結果",
  col = "black",
  bg = "white",
  
  lty = 1
)

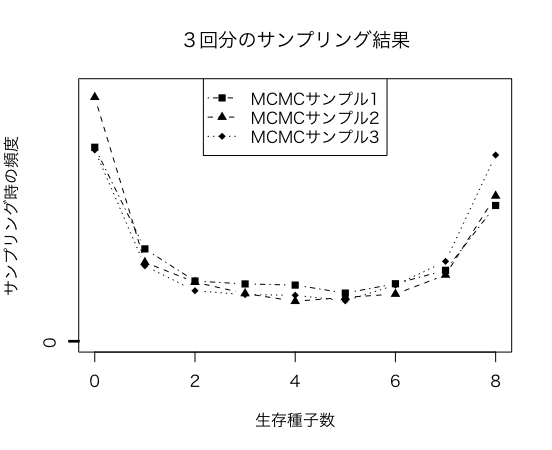
実行結果

サンプルとして3回実行です
4000サンプルの頻度となります

生存種子数(4000回)	MCMC1回目	MCMC2回目	MCMC3回目
0	1000	1257	986
1	478	409	391
2	313	307	263
3	298	249	243
4	292	209	240
5	251	229	211
6	299	246	292
7	368	344	414
8	701	750	960

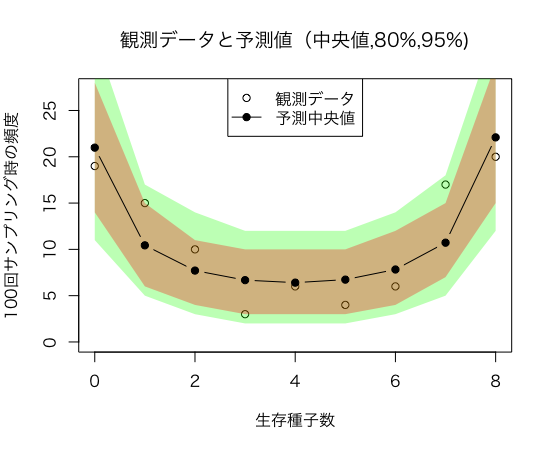
図10.4「生存種子数yの予測分布をstanで作成する

図10.4「生存種子数yの予測分布$p(Y|β,s)$と観測データ」の予測分布は予測する生存種子数yの分布ではなく、生存種子数(0..8)がそれぞれどの予測区間を表現している

図を作成するために予測分布を複数個(4000個）作成し、そこから生存種子数(0..8)それぞれの予測区間を求めている

##「パラメータを積分して周辺化版

「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル)」図 10.4: fig10_04.RをWinBugsからstanに改変するだけです

生存種子数ごとの確率(%)	2.5%パーセンタイル	10%パーセンタイル	50パーセンタイル%	90%パーセンタイル	97.5%パーセンタイル
0	0.14073058	0.16352565	0.20986948	0.25954604	0.29014848
1	0.08579645	0.09258903	0.10435539	0.11695097	0.12332079
2	0.06101239	0.06683494	0.07710027	0.08737962	0.09288967
3	0.05229914	0.05734506	0.06677069	0.07673788	0.08238204
4	0.04989203	0.05480968	0.06406959	0.07413396	0.07990446
5	0.05278356	0.05763164	0.06730962	0.07769051	0.08342632
6	0.06267173	0.06797085	0.07825451	0.08958981	0.09567091
7	0.08881159	0.09545877	0.10721223	0.12033319	0.12780923
8	0.15350783	0.17391524	0.22096061	0.27213672	0.30606913

fig10_04_to_Stan_integrate.R

library(rstan)
#install.packages("gtools")
library(gtools)

##################################
#積分する関数の定義
f.gaussian.binom <- function(alpha, x, size, fixed, sd)
  dbinom(x, size, logistic(fixed + alpha)) * dnorm(alpha, 0, sd)

#積分の呼び出し
d.gaussian.binom <- function(v.x, size, fixed, sd) sapply(
  #積分
  v.x, function(x) integrate(
    f = f.gaussian.binom,
    lower = -sd * 10,
    upper = sd * 10,
    # for f.gaussian.binom
    x = x,
    size = size,
    fixed = fixed,
    sd = sd
  )$value
)

##################
#生存種子数の頻度を表示
plot.data <- function() plot(
  0:size, 
  summary(as.factor(d$y)),#頻度
  ylim = range(c(0, dbinom(0:size, size, q) * n)),#Yの最大は27あたり
  xlab = "予測した生存種子数",
  ylab = "100回予測した時の頻度",
  pch = 19#黒丸
)
#予測区間をポリゴンで描画
plot.polygon <- function(mm, p)
{
  pp <- 1 - p
  qp <- apply(mm, 1, quantile, probs = c(0.5 * pp, 1 - 0.5 * pp))
  polygon(
    c(0:size, size:0),
    c(qp[1,], rev(qp[2,])),
    border = NA,
    col = "#00000020"
  )
}
#生存種子数ごとの頻度をラインでむすぶ
plot.lines <- function(mm)
{
  apply(
    mm, 2,
    function(x) lines(0:size, x, col = "#00000001", lwd = 2)
  )
}
#事後確率最大推定値の頻度を表示
plot.median <- function()
{
  lines(
    0:size, apply(mp * n, 1, median),
    type = "b",
    col = "black",
    bg = "white",
    pch = 21
  )
}
##################################
#main
d <- read.csv('http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/data7a.csv')
#setwd("~/work/StanR/RStanBook/chap08/exercise")
##################################
###Stanでサンプリング
data <- list(N=nrow(d), Y=d$y)
fit <- stan(file='ex6.stan', data=data, seed=1234)
ms <- rstan::extract(fit)
##################################
#予測
logistic <- function(z) 1 / (1 + exp(-z))
n <- nrow(d)
size <- 8
q <- sum(d$y) / (size * n)

######
#Stanの結果代入
beta <- ms$b
sigma <- ms$s_I

cat("# generating mp（事後確率最大推定値 ")
mp <- sapply(
  1:nrow(beta),
  function(i) {
    if (i %% 100 == 0) cat(".")
    d.gaussian.binom(
      0:size, size,
      fixed = beta[i],
      sd = sigma[i]
    )
  }
)
#
my <- apply(
  mp, 2, function(prob) summary(
    factor(
      sample(0:size, n, replace = TRUE, prob = prob),
      levels = 0:size
    )
  )
)

##################################
par(family = "HiraKakuProN-W3")
plot.data()
#95%予測区間
q.env95 <- apply(my, 1, quantile, probs = c(0.025, 0.975))
polygon(
  c(0:size, size:0),
  c(q.env95[1,], rev(q.env95[2,])), # 0.025 and 0.975
  border = FALSE,
  col = "#00000020"
)
#80%予測区間
q.env80 <- apply(my, 1, quantile, probs = c(0.1, 0.9))
polygon(
  c(0:size, size:0),
  c(q.env80[1,], rev(q.env80[2,])), # 0.025 and 0.975
  border = FALSE,
  col = "#00000010"
)
plot.median()

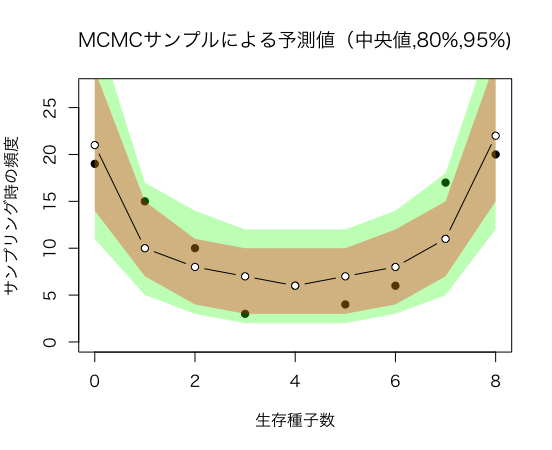
パラメータから乱数を作り、新たな分布を作成

「パラメータを積分して周辺化」している部分をStanのMCMCサンプル結果抽出するだけなので一行ですみます。

予測区間を比較すると大体あってそうです

生存種子数ごとの確率(%)	2.5%パーセンタイル	10%パーセンタイル	50パーセンタイル%	90%パーセンタイル	97.5%パーセンタイル
0	0.1412437	0.162475	0.21075	0.264275	0.2935000
1	0.0840000	0.090725	0.10475	0.119025	0.1262500
2	0.0605000	0.065500	0.07700	0.089000	0.0950000
3	0.0507500	0.056250	0.06675	0.077750	0.0842500
4	0.0485000	0.053500	0.06400	0.074775	0.0815000
5	0.0512500	0.056250	0.06725	0.078750	0.0847500
6	0.0607500	0.066250	0.07775	0.090000	0.0962500
7	0.0857500	0.093000	0.10700	0.121750	0.1302563
8	0.1507500	0.172725	0.21950	0.274250	0.3090063

fig10_04_to_Stan.R

library(rstan)
#install.packages("gtools")
library(gtools)


##################
#dummy
plot.data <- function() plot(
  0:size, 
  summary(as.factor(d$y)),#頻度
  ylim = range(c(0,27)),#
  xlab = "生存種子数",
  ylab = "サンプリング時の頻度",
  #col = "white",
  pch = 19,#黒丸,
  main="MCMCサンプルによる予測値（中央値,80%,95%)"
  
)
#予測区間をポリゴンで描画
plot.polygon <- function(mm, p)
{
  pp <- 1 - p
  qp <- apply(mm, 1, quantile, probs = c(0.5 * pp, 1 - 0.5 * pp))
  polygon(
    c(0:size, size:0),
    c(qp[1,], rev(qp[2,])),
    border = NA,
    col = "#00000020"
  )
}
#生存種子数ごとの頻度をラインでむすぶ
plot.lines <- function(mm)
{
  apply(
    mm, 2,
    function(x) lines(0:size, x, col = "#00000001", lwd = 2)
  )
}
#事後確率最大推定値の頻度を表示
plot.median <- function(mm)
{
  lines(
    0:size, apply(mm , 1, median),
    type = "b",
    col = "black",
    bg = "white",
    pch = 21
  )
}
##################################
#main
d <- read.csv('http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/data7a.csv')
setwd("~/work/StanR/RStanBook/chap08/exercise")
##################################
###Stanでサンプリング
##################################
data <- list(N=nrow(d), Y=d$y)
fit <- stan(file='ex6_base.stan', data=data, seed=1234)
ms <- rstan::extract(fit)

##################################
###Stanでサンプリング
##################################
#サンプル数4000なので確率にするため4000で割る
d1 <- apply(ms$y_pred, 1, table)[]/4000

##################################
###予測区間の描画
##################################
my <- apply(
  d1, 2, function(prob) summary(
    factor(
      sample(0:size, n, replace = TRUE, prob = prob),
      levels = 0:size
    )
  )
)
#summary( apply(d1, 2, prop.table))
#smy <- t(apply(d1, 1, quantile, probs = c(0.025,0.1,0.5,0.9,0.975)))


par(family = "HiraKakuProN-W3")
plot.data()
#95%予測区間
q.env95 <- apply(my, 1, quantile, probs = c(0.025, 0.975))
polygon(
  c(0:size, size:0),
  c(q.env95[1,], rev(q.env95[2,])), # 0.025 and 0.975
  border = FALSE,
  col=rgb(0, 1, 0,0.3)
)
#80%予測区間
q.env80 <- apply(my, 1, quantile, probs = c(0.1, 0.9))
polygon(
  c(0:size, size:0),
  c(q.env80[1,], rev(q.env80[2,])), # 0.025 and 0.975
  border = FALSE,
  col=rgb(1, 0, 0,0.3)
)
plot.median(my)

まとめ

「データ解析のための統計モデリング(一般化線形モデル・階層ベイズモデル・MCMC)」の図10.4「生存種子数yの予測分布$p(Y|β,s)$と観測データ」がなんなのかを理解できないためまとめました
結果を比較する限り元のソースと同じ結果が取れたため、理解が間違っていないと考え公開しましたが、間違えがあればご指摘ください

Stanを用いれば、予測区間はo信頼区間と同様にMCMCでサンプル結果から求めることがわかりました
このまとめを書くことでベイズ推定の凄さがわかりました、また勉強期間１週間でようやく初心者から中級者の入り口くらいに到達したとおもうのでベイジアンと名乗りたいです