これはHaskell Advent Calendar 2013の16日目の記事です。突っ込み・コメントなど歓迎します。
HLearnは、代数的構造を利用した統計・機械学習ライブラリということで、型の表現力が豊かであるHaskellの面目躍如の分野と言えそうだ。代数的構造に着目することで、同じ代数的構造を持つデータはその詳細によらず共通の抽象化を使えるというメリットがある。
まだ実験レベルのライブラリでAPIが頻繁に変わり、機能も多くないが、コンセプトが面白そうだったのでどういうふうに使えるか見てみた。
特徴
- データポイントからモデル(統計分布、分類など)を計算。
- 確率分布(多変数正規分布、指数分布、二項分布、ポアソン分布、など)
- 分類(単純ベイズ、K近傍法、パーセプトロン、など)
- マルコフ連鎖
- この論文 のTable 3に実装されているアルゴリズムのリストがある。
- データポイントからモデルを生成した後、モデルの更新がデータポイントの数によらず高速にできる。
- ロジックを非常に簡潔に書け、さまざまな学習器(バッチ、オンライン、並列)を自動で生成。
- http://izbicki.me/blog/hlearns-code-is-shorter-and-clearer-than-wekas
また、これらの実装済みのアルゴリズム以外でも、一般にHomTrainer型クラス(後述)のインスタンスとなるアルゴリズムを用意してやれば、HLearnの枠組みが使える。
インストール・使用例
sudo cabal install HLearn-classification
なのだが、僕の環境だとコンパイルに失敗した。Githubのレポをクローンしてそこからcabal installでインストールできた(Github issue)。
確率分布の計算
数値データ
import HLearn.Models.Distributions
import HLearn.Algebra.Models.HomTrainer
dataset = [1,2,3,4,5,6]
dist = train dataset :: Normal Integer Integer
非数値データの分布
-- 引用元: http://izbicki.me/blog/functors-and-monads-for-analyzing-data
-- いろいろな色のビー玉の定義
data Marble = Red | Pink | Green | Blue | White
deriving (Read,Show,Eq,Ord)
bagOfMarbles = [ Pink,Green,Red,Blue,Green,Red,Green,Pink,Blue,White ]
-- カテゴリーデータ(このカテゴリーというのは離散変数・非数値データという意味で、圏論とは無関係の用語(https://en.wikipedia.org/wiki/Categorical_distribution))
marblesDist :: Categorical Double Marble
marblesDist = train bagOfMarbles
-- EPSで出力
plotMarbles = plotDistribution (plotFile "output" EPS) marblesDist
-- ビー玉の重さ
marbleWeight :: Marble -> Int -- weight in grams
marbleWeight Red = 3
marbleWeight Pink = 2
marbleWeight Green = 3
marbleWeight Blue = 6
marbleWeight White = 2
-- 重さの分布
weightsDist :: Categorical Double Int
weightsDist = train $ map marbleWeight bagOfMarbles
-- 作者のブログにある例なのだが、なぜかNo instance for (Functor (Categorical Double))と言われコンパイルできない。
-- weightsDist == weightsDist'になるはずである。
-- weightsDist' :: Categorical Double Int
-- weightsDist' = fmap marbleWeight marblesDist
plotWeights = plotDistribution (plotFile "weightsDist" EPS) weightsDist
分類
HLearn-classificationパッケージなのだが、例が見つからず使い方が不明。後ほど追記予定。
その他
変わり種として、NP困難問題である Bin packing problem の近似解法。このMonad Readerの記事で解説されている。
解説記事
以下全て英語。ライブラリ作者による論文とチュートリアルがある。
-
色々リンクが貼ってある。
-
http://themonadreader.files.wordpress.com/2013/08/issue221.pdf
-
Two Monoids for Approximating NP-Complete Problems (The Monad.Reader Issue 22)という記事。
-
http://faculty.cs.byu.edu/~jay/conferences/2013-tfp/proceedings/tfp2013_submission_10.pdf
-
2013年の論文。
-
2013年の論文。K-foldの交差検定が、通常ではO(kn)であるところを、HLearnを使うとO(k+n)の計算量でできるという話。
-
http://izbicki.me/blog/functors-and-monads-for-analyzing-data
-
モデルがファンクタになっていて、一旦モデルを生成した後の元データの変更という操作を表現できる。
-
さらに、元データに変更があったときのモデルの更新が単純にモデルを更新するよりも高速にできる。
ちなみに、一般的に代数的構造からアルゴリズムを導くという話は、Algebra of Programming で議論されている。
(しばらく前に買ったが、難しすぎて挫折中。どなたか一緒に読書会でもやりませんか。)
内部構造: 基本の型クラス HomTrainer
HomTrainerクラスがHLearn.Algebra.Models.HomTrainer モジュールに定義されていて、これが核となる。
この型クラスは、「 フリーモノイドからのモノイドモノモーフィズム」であるアルゴリズムを表す。この圏論の言葉の意味はよく分からないが、指していることは単純で、
- 細切れのデータセットからそれぞれに対応するモデルを計算し、そのモデルを後から合算して一つの最終的なモデルを計算する。
- 細切れのデータセットを最初に集約して、そのデータセットから1つのモデルを計算する。
これらの、モデル計算と集計の順番が入れ替わっている2つのルートが同じ結果を与える。
という条件である。学習(モデル計算)と集計が可換という条件と言ってもよい。
わりと強い条件ではあるが、この条件を満たす場合に、HomTrainerが良きに計らってくれて、さまざまな学習モードが自動的に定義される。
HomTrainerの基本となるのは以下の4つのメソッドである。オンライン学習、バッチ学習などのメソッドがある。
--HomTrainerのモデルはモノイドなので、結果をmappendで合算できる。
class Monoid model => HomTrainer model where
-- シングルトン学習器
train1dp :: HomTrainer model => Datapoint model -> model
-- バッチ
train :: (Functor container, Foldable container) => container (Datapoint model) -> model
-- オンライン(データポイントの漸次的な追加)
add1dp :: model -> Datapoint model -> model
-- オンラインバッチ
addBatch :: (Functor container, Foldable container) => model -> container (Datapoint model) -> model
ここで、Datapoint model型はtype familyなので、HomTrainerクラスのインスタンスごとに異なる型を持つ(type familyとは、型クラスのメソッドが、インスタンスごとに異なる型シグネチャを持てるようにする仕組み。インスタンス宣言の中でDatapoint modelの実際の型を指定する。)。
以下に挙げる関係によってこれら4つのメソッドは変換可能である(画像は論文より引用)。つまり、どれか一つのメソッド(とそれに加え、モデルのモノイドのインスタンス定義)を定義すればあとは自動で定義される。
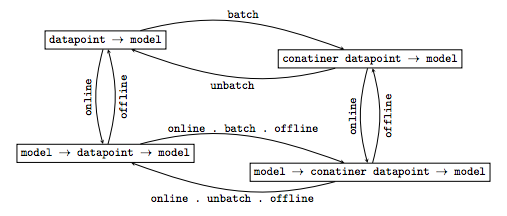
そして、先に挙げたMarbleの例の場合、モデルにfmap fを掛けてモデルを変更するときに、その計算量が元データのデータポイントの数によらず、集計後のモデルに出現するMarbleの数にのみ依存する。
以上がHLearnライブラリのキモである。作者いわく、この枠組に当てはまるアルゴリズムを探索し実装するのが作者の今後の計画だということである。なお、2013年のライブラリの作者の論文によれば、既存の統計・機械学習モデルがHomTrainerのようなきれいな代数的構造を持つかどうかというのは大部分は未解明とのことである。
まとめ
統計やデータ処理を代数的構造によって定義することで自動で効率的なアルゴリズムを生成するというのは非常に興味深い。ソースコードも非常に簡潔であるし、コードの再利用性も高くなると思われる。個人的には、こういった概念の生物などの画像処理への応用にも興味がある。