http://scikit-learn.org/0.18/modules/decomposition.html を google翻訳した
2.5. コンポーネント内の信号を分解する(行列分解問題)
2.5.1. 主成分分析(PCA)
2.5.1.1. 正確なPCAと確率論的解釈
PCAは、分散の最大量を説明する連続する直交成分の集合における多変量データセットを分解するために使用される。 scikit-learnでは、 PCA はn個のコンポーネントを fit メソッドで学習し、これらのコンポーネントに新しいデータを使用してこれらのコンポーネントに投影するトランスフォーマーオブジェクトとして実装されています。
オプションのパラメータ whiten = True を使用すると、各コンポーネントを単位分散にスケーリングしながら、データを特異空間に投影することができます。 モデルのダウンストリームが信号の等方性を強く前提とする場合、これはしばしば有効です。これは、例えば、RBFカーネルとK-Meansクラスタリングアルゴリズムを使用したサポートベクターマシンの場合です。
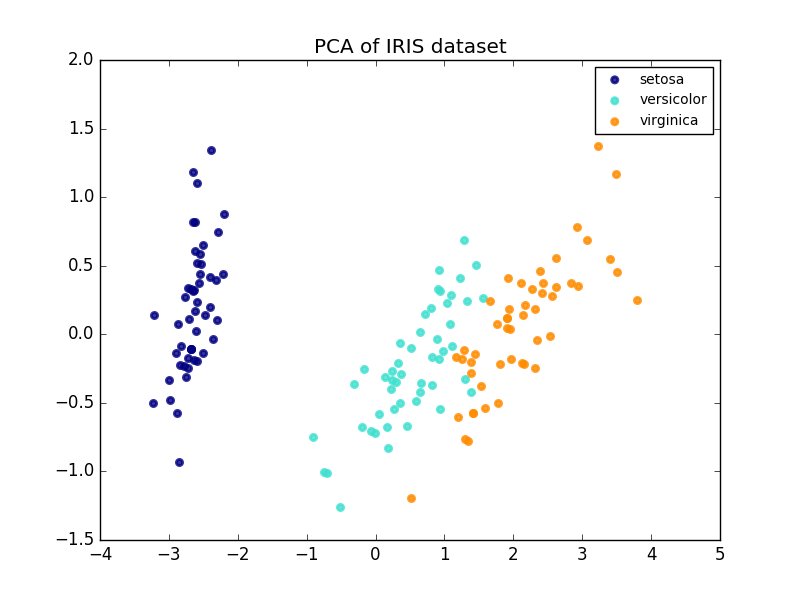
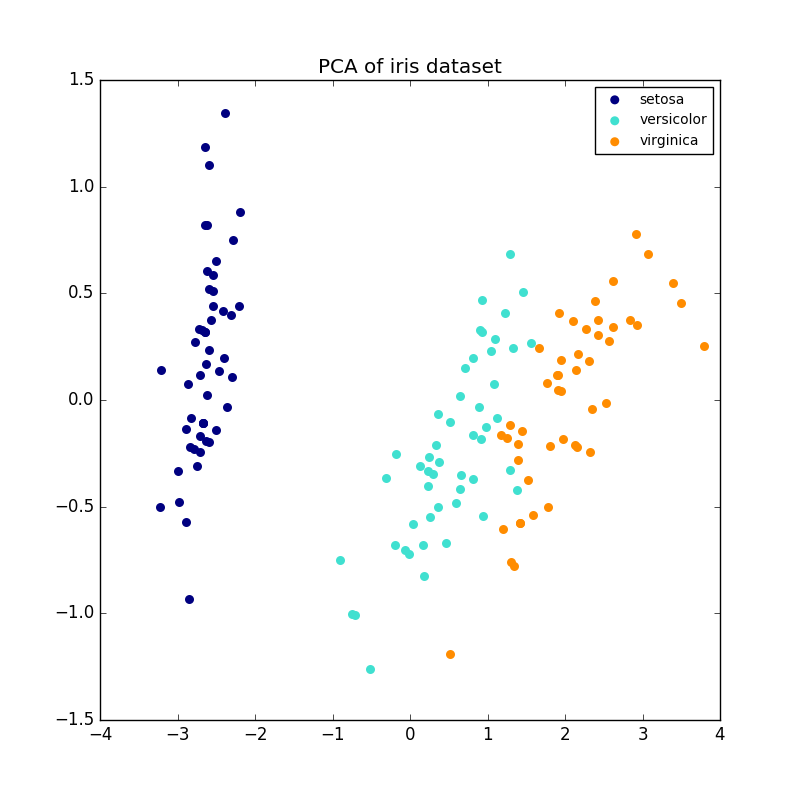
以下は、アイリスデータセットの例です。これは、4つのフィーチャで構成され、2つのディメンションに投影され、ほとんどの分散が説明されています。
PCAオブジェクトはまた、PCAの確率論的解釈を提供し、PCAは、それが説明する分散量に基づいてデータの可能性を与えることができる。このように、相互認証に使用できるスコアメソッドを実装しています。
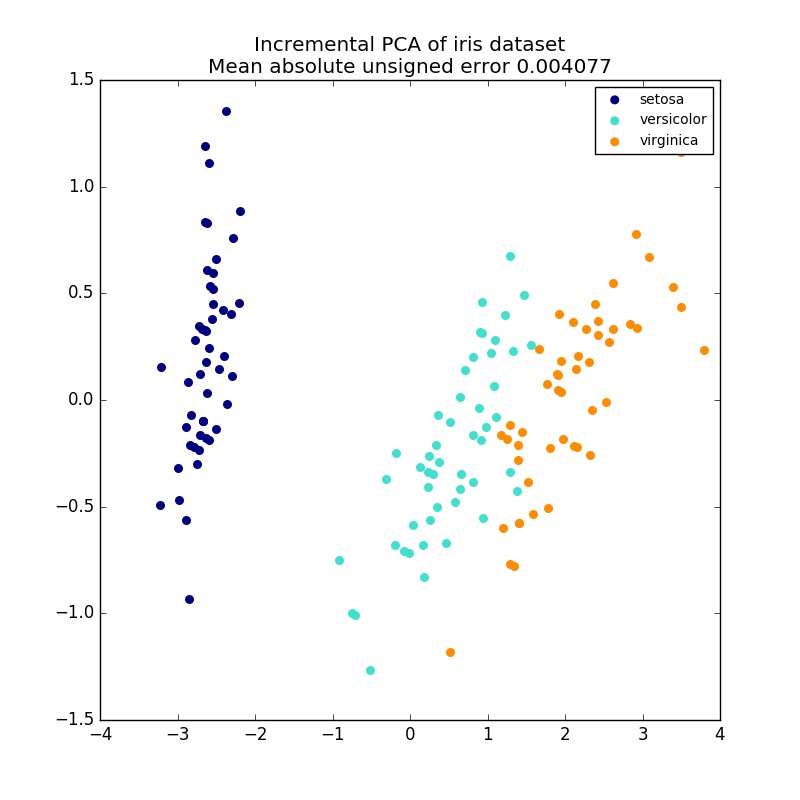
2.5.1.2. インクリメンタルPCA
PCA オブジェクトは非常に便利ですが、大きなデータセットには一定の制限があります。 PCAはバッチ処理のみをサポートしているため、処理されるすべてのデータがメインメモリに収まる必要があります。 IncrementalPCA オブジェクトは、異なる形式の処理を使用し、PCAの結果とほぼ正確に一致する部分的な計算を可能にし、ミニバッチの方法でデータを処理します。 IncrementalPCAを使用すると、次のいずれかの方法でコア外の主成分分析を実装することができます。
- ローカルハードドライブまたはネットワークデータベースから順番にフェッチされたデータのチャンクに対して
partial_fitメソッドを使用します。 -
numpy.memmapを使用してメモリマップされたファイルにfitメソッドを呼び出します。
IncrementalPCAはコンポーネントとノイズの分散の推定値を格納しているだけで、 explain_variance_ratio_ を段階的に更新します。 このため、メモリ使用量は、データセットで処理されるサンプル数ではなく、バッチあたりのサンプル数に依存します。
- 例:
2.5.1.3. ランダム化SVDを用いたPCA
より特異な値に関連付けられたコンポーネントの特異ベクトルを削除することによって、ほとんどの分散を保存する低次元空間にデータを投影することは、しばしば興味深いことです。
例えば、顔認識のために64×64画素のグレイレベル画像を扱う場合、データの次元は4096であり、このような広いデータに対してRBFサポートベクトルマシンを訓練するのは遅い。さらに、人間の顔のすべての画像が幾分似ているので、データの固有次元が4096よりはるかに小さいことがわかります。サンプルは、はるかに低い次元(例えば、約200など)の多様体上にある。 PCAアルゴリズムを使用すると、データを線形変換することができ、同時に次元を減らし、説明された分散の大部分を保存することができます。
オプションパラメータ svd_solver = 'randomized' で使用されるPCAクラスは、そのような場合に非常に便利です。ほとんどの特異ベクトルを削除するので、計算を特異ベクトルの近似推定値に限定する方がはるかに効率的です。実際に変換を実行してください。
たとえば、Olivettiデータセットからの16のサンプル肖像画(0.0を中心に)を以下に示します。右側には、ポートレートとして再構成された最初の16個の特異ベクトルがあります。 $ n_{samples} = 400$ と $n_{features} = 64 \times 64 = 4096$ のデータセットの上位16個の特異ベクトルのみが必要なので、計算時間は1秒未満です。
注意:オプションパラメータ svd_solver = 'randomized' を使用して、必須入力パラメータとして低次元空間 n_components のサイズをPCAに与える必要もあります。
$n_{max} = max(n_{samples}, n_{features})$ と $n_{min} = min(n_{samples}, n_{features})$ に注目すると、ランダム化PCAの時間複雑さは、PCAで実装された正確な方法では $O(n_{max}^2 \cdot n_{components})$ ではなく $O(n_{max}^2 \cdot n_{min})$ です。
ランダム化されたPCAのメモリフットプリントは、正確な方法では $n_{max}
\cdot n_{min}$ の代わりに $2 \cdot n_{max} \cdot n_{components}$ に比例します。
注: svd_solver = 'randomized' を使用したPCAでの inverse_transform の実装は、 whiten = False(デフォルト)の場合でも transform の正確な逆変換ではありません。
- 例:
- 参考文献:
- ランダム性を有する構造を見つける:近似行列分解を構築するための確率的アルゴリズム Halko、et al。、2009
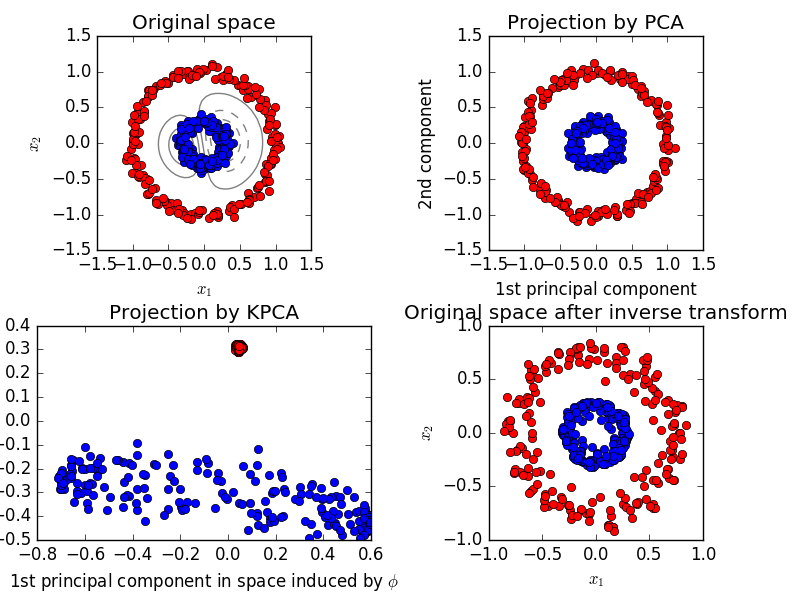
2.5.1.4. カーネルPCA
KernelPCA は、カーネルの使用によって非線形次元削減を実現するPCAの拡張です( ペアメトリック、アフィニティーおよびカーネル を参照)。それには、ノイズ除去、圧縮、構造化予測(カーネル依存性推定)などの多くのアプリケーションがあります。 KernelPCAは、 transform と inverse_transform の両方をサポートします。
- 例:
2.5.1.5. まばらな主成分分析(SparsePCAおよびMiniBatchSparsePCA)
SparsePCAは、データを最もよく再構成する疎なコンポーネントのセットを抽出する目的で、PCAの変種です。
ミニバッチスパースPCA( MiniBatchSparsePCA )は、SparsePCAの変形であり、高速ですが精度は劣ります。増加した速度は、指定された回数の反復に対して、フィーチャセットの小さなチャンクを反復することによって達成されます。
主成分分析(PCA)は、この方法によって抽出された成分が独占的に濃密な表現を有する、すなわち元の変数の線形結合として表現されたとき非ゼロ係数を有するという欠点を有する。これは解釈を困難にする可能性があります。多くの場合、実際の基礎となるコンポーネントは、より自然に疎ベクトルとして想像することができます。例えば顔認識では、コンポーネントは自然に顔の一部にマッピングされることがあります。
スパースな主成分は、元の特徴のどれがサンプル間の差異に寄与するかを明確に強調し、より簡潔で解釈可能な表現をもたらす。
次の例は、OlivettiフェイスのデータセットからSparsePCAを使用して抽出された16のコンポーネントを示しています。正規化項がどのように多くのゼロを誘導するかを見ることができます。さらに、データの自然な構造は、非ゼロ係数を垂直に隣接させる。モデルは、これを数学的に強制するわけではありません。各構成要素はベクトル $h \in \mathbf{R}^{4096}$ であり、64 x 64ピクセル画像のような人に優しい視覚化の間を除いて、垂直隣接の概念はありません。以下に示す構成要素が局所的に現れるという事実は、データの固有の構造の影響であり、そのような局所パターンは再構成誤差を最小限にする。隣接性とさまざまな種類の構造を考慮した希薄性を誘導する規範が存在する。そのような方法のレビューについては、 [Jen09] を参照してください。スパースPCAの使用方法の詳細については、下記の例のセクションを参照してください。
SparsePCA 問題には多くの異なる式が存在することに注意してください。ここで実装されているのは[Mrl09]に基づいています。解決された最適化問題は、PCA問題(辞書学習)であり、コンポーネント上に $\ell_1$ のペナルティがあります。
(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
||X-UV||_2^2+\alpha||V||_1 \\
\text{subject to\,} & ||U_k||_2 = 1 \text{ for all }
0 \leq k < n_{components}
スパース性を誘導する $\ell_1$ ノルムは、利用可能な訓練サンプルがほとんどない場合、学習コンポーネントのノイズからの保護も防ぎます。ペナルティの程度(したがってスパース性)は、ハイパーパラメータ alpha を介して調整することができる。小さな値は緩やかに正則化された因数分解をもたらし、大きな値は多くの係数をゼロに縮めます。
注意: オンラインアルゴリズムの中で、 MiniBatchSparsePCA クラスは partial_fit を実装していませんが、アルゴリズムはサンプル方向ではなく、特徴方向に沿ってオンラインであるためです。
- 例:
- 参考文献:
- [Mrl09] スパースコーディングのためのオンライン辞書学習 J. Mairal、F. Bach、J. Ponce、G.Sapiro、2009
- [Jen09] 構造化スパース主成分分析 R. Jenatton、G. Obozinski、F. Bach、2009
2.5.2. 切り捨て特異値分解と潜在意味解析
TruncatedSVD は、 $k$ がユーザ指定のパラメータである $k$ 個の最大特異値のみを計算する特異値分解(SVD)の変形を実装します。
切り捨てられたSVDが( CountVectorizer または TfidfVectorizer によって返される)term-document行列に適用されるとき、この変換は 潜在意味解析(latent semantic analysis:LSA) として知られている。行列を低次元の「意味論的」空間に変換するためです。特に、LSAは、同義語や多義語(どちらもおおまかに言えば、複数の意味があることを意味する)の効果と戦うことが知られています。これは、用語文書行列が過度に疎であり、コサイン類似性などの手段で類似性が低いことを示します。
注意: LSAは潜在意味索引付け、LSIとも呼ばれますが、厳密には情報検索目的で永続インデックスに使用されることを指します。
数学的には、訓練サンプル $X$ に適用された truncated SVD は、低ランク近似 $X$ を生成する。
X \approx X_k = U_k \Sigma_k V_k^\top
この操作の後、 $U_k\Sigma_k^\top$ は $k$ 個の特徴量(APIで n_components と呼ばれます)を持つ変換された訓練セットです。
また、テスト集合 $X$ を変換するために、 $V_k$ を乗算します。
X' = X V_k
注意: 自然言語処理(NLP)および情報検索(IR)の文献でのLSAのほとんどの処理は、行列 $n$ の軸をスワップして n_features × n_samples という形を持つようにします。我々はscikit-learn APIによくマッチする異なる方法でLSAを提示しますが、見つかった特異値は同じです。
TruncatedSVD は PCAと非常によく似ていますが、共分散行列ではなくサンプル行列 $X$ で直接動作するという点で異なります。列方向(特徴ごと)の $X$ の平均を特徴量から差し引くと、結果として得られる行列上の切り捨てられたSVDはPCAと等価である。実際には、これは、TruncatedSVD変換器が、密度の高密度化が中規模の文書コレクションであってもメモリをいっぱいにする可能性があるため、 scipy.sparse 行列を高密度化せずに受け入れることを意味します。
TruncatedSVD 変換器は任意の(疎な)特徴行列で動作しますが、 tf-idf行列 での使用は、LSA/ドキュメント処理設定の未処理の頻度カウントよりも推奨されます。特に、テキストデータに関するLSAの誤った仮定を補うために、特徴量値をガウス分布に近づけるために、サブ線形スケーリングと逆ドキュメント頻度をオンにする必要があります( sublinear_tf = True 、use_idf = True )。
- 例:
- 参考文献:
- Christopher D. Manning、Prabhakar Raghavan and HinrichSchütze(2008)、ケンブリッジ大学出版会、第18章: マトリックス分解と潜在意味索引付け
2.5.3. 辞書学習
2.5.3.1. あらかじめ計算された辞書によるスパースコーディング
SparseCoder オブジェクトは、信号を離散ウェーブレットベースなどの固定された事前計算された辞書からの疎な線形結合に変換するために使用できる推定器です。したがって、このオブジェクトは fit メソッドを実装しません。この変換は、疎な符号化問題になります。可能な限り少数の辞書アトムの線形結合としてデータの表現を見つけることです。辞書学習のすべてのバリエーションは、 transform_method 初期化パラメータを介して制御可能な以下の変換方法を実装しています。
- 直交マッチング追求( OMP:Orthogonal Matching Pursuit)
- 最小角度回帰( 最小角度回帰 )
- 最小角回帰によって計算されたラッソ
- 座標降下(ラッソ)を使用するラッソ ( Lasso )
- しきい値
しきい値は非常に高速ですが、正確な再構成はできません。それらは、分類作業のための文献において有用であることが示されている。画像再構成タスクのために、直交マッチング追跡は最も正確で不偏な再構成をもたらす。
辞書学習オブジェクトは、 split_code パラメータを介して、スパース符号化の結果における正の値と負の値とを分離する可能性を提供する。これは、学習アルゴリズムが特定の原子の負の負荷に対応する正の負荷から負の負荷に異なる重みを割り当てることを可能にするため、教師あり学習に使用される特徴を抽出するために辞書学習を使用する場合に便利です。
1つのサンプルの分割コードは 2 * n_components の長さを持ち、次の規則を使用して作成されます。まず、長さ n_components の通常のコードが計算されます。次に、 split_code の最初の n_components エントリは、正規コードベクトルの正の部分で埋められます。分割コードの後半は、正の符号のみでコードベクトルの負の部分で埋められます。したがって、 split_code は負ではありません。
2.5.3.2. 一般的な辞書学習
辞書学習( DictionaryLearning )は、適合したデータをまばらに符号化することで良好に機能する(通常は過度の)辞書を見つけることに相当する行列分解問題である。
オーバーコンプリート辞書からの原子の希薄な組み合わせとしてデータを表現することは、哺乳類の主要な視覚野の働きを示唆している。その結果、画像パッチに適用された辞書学習は、画像補完、修復およびノイズ除去、ならびに監視された認識タスクのような画像処理タスクにおいて良好な結果を与えることが示されている。
辞書学習は、複数のラッソ問題の解決策として、疎コードを代替的に更新し、辞書を修正して疎コードに最もよく適合するように辞書を更新することによって解決される最適化問題である。
(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
||X-UV||_2^2+\alpha||U||_1 \\
\text{subject to\,} & ||V_k||_2 = 1 \text{ for all }
0 \leq k < n_{atoms}
このような手順を使用して辞書に適合させた後、変換は、すべての辞書学習オブジェクトと同じ実装を共有する単純なコーディングステップです( 事前計算された辞書によるスパースコーディング を参照)。
次の画像は、アライグマの顔の画像の一部から抽出された4x4ピクセル画像パッチから辞書がどのようにして学習されたかを示しています。
- 例:
- 参考文献:
- "スパースコーディングのためのオンライン辞書学習" J. Mairal、F. Bach、J. Ponce、G.Sapiro、2009
2.5.3.3. ミニバッチ辞書学習
MiniBatchDictionaryLearning は、大規模なデータセットに適した辞書学習アルゴリズムのより高速ではあるが精度の低いバージョンを実装します。
デフォルトでは、MiniBatchDictionaryLearningはデータをミニバッチに分割し、指定された反復回数だけミニバッチを循環させることによってオンラインで最適化します。しかし、現時点では停止状態を実装していません。
また、推定器は partial_fit を実装しています。これは、ミニバッチで一度だけ繰り返して辞書を更新します。これは、データが最初から容易に利用できない場合、またはデータがメモリに収まらない場合にオンライン学習に使用できます。
辞書学習のためのクラスタリング
表現を抽出するために辞書学習を使用するとき(例えば疎コーディングの場合)、クラスタリングは辞書を学習する良いプロキシであり得ることに留意されたい。例えば、 MiniBatchKMeans 推定器は計算上効率的であり、 partial_fit 法を用いてオンライン学習を実施する。
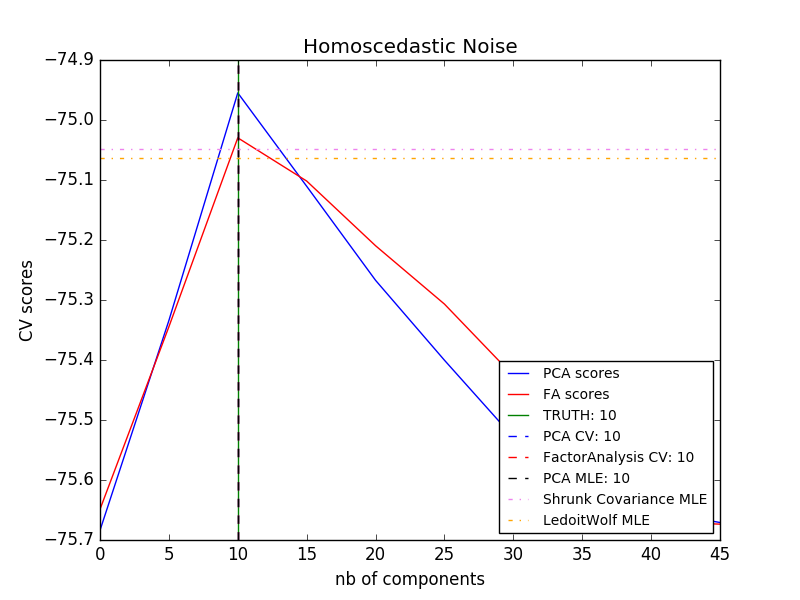
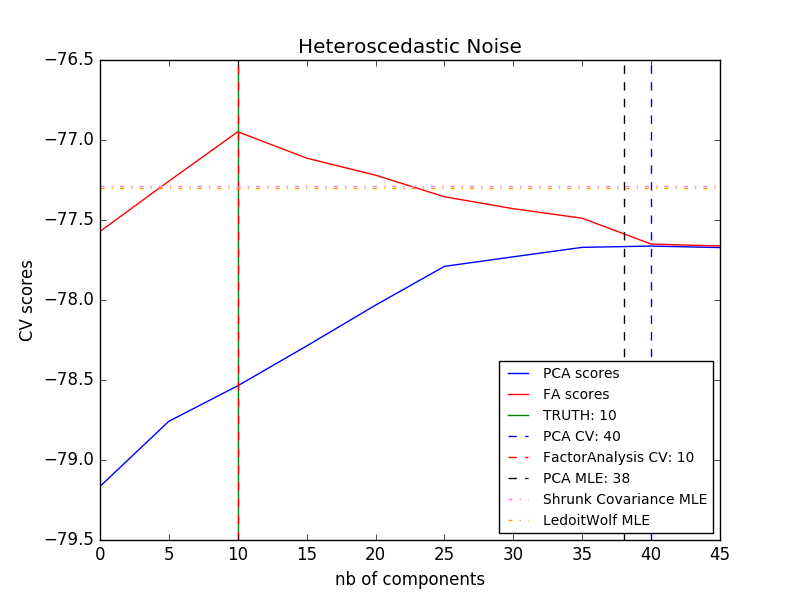
2.5.4. 因子分析
教師なし学習では、データセットは $X = {x_1, x_2, \dots, x_n
}$ しかない。このデータセットはどのように数学的に記述できるか? 非常に単純な連続潜在変数モデルでは $X$ は、
x_i = W h_i + \mu + \epsilon
ベクトル $h_i$ は観察されないので「潜伏(latent)」と呼ばれる。 $ε$ は、平均 0 、共分散 $\Psi$(すなわち、 $\epsilon \sim \mathcal{N}(0, \Psi))$ )を有するガウス分布に従って分布されたノイズ項と見なされ、 $μ$ は任意のオフセットベクトルである。そのようなモデルは、 $h_i$ から $x_i$ がどのように生成されるかを記述するので、「生成的(generative)」と呼ばれます。すべての $x_i$ を列として使用して行列 $\mathbf{X}$ を作成し、すべての $h_i$ を行列 $\mathbf{H}$ の列として使用すると、(適切に定義された $\mathbf{M}$ と $\mathbf{E}$ を使用して)次のように書くことができます:
\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}
言い換えれば、行列 $\mathbf{X}$ を分解した。
$h_i$ が与えられると、上記の式は自動的に以下の確率的解釈を意味する。
p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)
完全確率モデルの場合、潜在変数 $h$ に対する事前分布も必要である。ガウス分布の良い特性に基づく最も単純な仮定は、$h \sim \mathcal{N}(0,
\mathbf{I})$ です。これは、 $x$ の限界分布としてガウス分布を生成する:
p(x) = \mathcal{N}(\mu, WW^T + \Psi)
さて、さらなる仮定なしに、潜在変数 $h$ を持つ考えは余計なものになるでしょう。 $x$ は平均と共分散で完全にモデル化できます。これら2つのパラメータのうちの1つに、より具体的な構造を課す必要があります。シンプルな追加の仮定は、誤差共分散 $\Psi$ の構造に関する:
- $\Psi = \sigma^2 \mathbf{I}$ :この仮定はPCAの確率論的モデルにつながる。
- $\Psi = diag(\psi_1, \psi_2, \dots, \psi_n)$ :このモデルは古典的な統計モデルである 因子分析 FactorAnalysis と呼ばれます。行列Wは、「因子負荷行列」と呼ばれることがあります。
両方のモデルは、本質的に、低ランクの共分散行列を有するガウス分布を推定する。両方のモデルは確率的なので、より複雑なモデルに統合することができます。例えば因子分析同士の組み合わせ等。潜在変数上の非ガウス型事前確率が想定される場合、非常に異なるモデル(例えば FastICA )を得る。
因子分析は、類似の成分(その負荷マトリックスのカラム)を PCA に生成することができる。しかしながら、これらの構成要素に関する一般的な記述(例えば、それらが直交しているかどうか)を行うことはできない。
PCA に対する因子分析の主な利点は、入力空間のすべての方向で分散を個別にモデル化できることです(信号値比例変動型(heteroscedastic)ノイズ)。
これは、異方性雑音の存在下での確率的PCAよりも優れたモデル選択を可能にする。
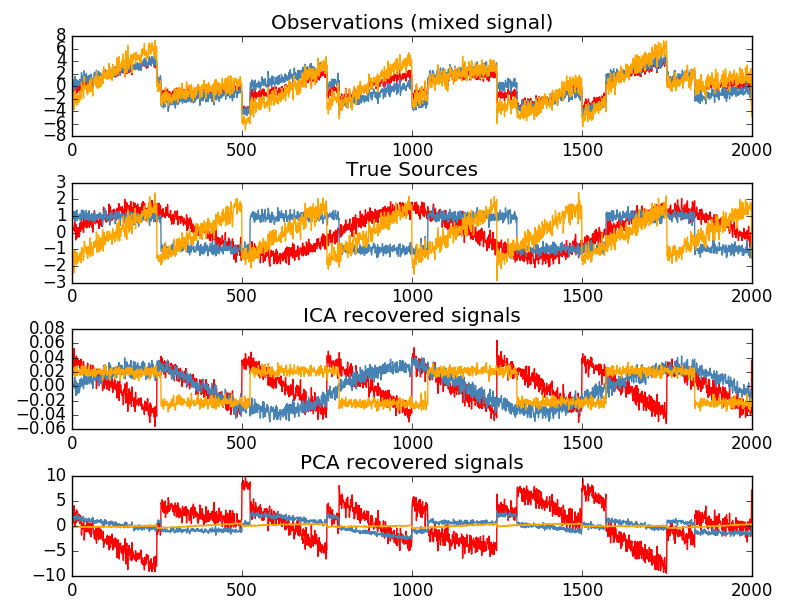
2.5.5. 独立成分分析(ICA)
独立成分分析は、多変量信号を最大限独立した加法サブ成分に分離します。 FastICA アルゴリズムを使用してscikit-learnで実装されています。 典型的には、ICAは次元性を低下させるためではなく、重畳信号を分離するために使用される。 ICAモデルにはノイズ項が含まれていないため、モデルが正しいためには、ホワイトニングを適用する必要があります。 これはwhiten引数を使用して内部的に、またはPCAまたはその変形の1つを使用して手動で行うことができます。
これは、以下の例のように、混合信号を分離するために古典的に使用されます(ブラインド音源分離と呼ばれる問題)。
ICAはまた、まばらな構成要素を見つけるさらに別の非線形分解としても使用できます。


2.5.6. 非負行列分解(NMFまたはNNMF)
2.5.6.1. フロベニウスノルムを持つNMF
NMF は、データとコンポーネントが非負であることを前提とした分解の代替アプローチです。データ行列に負の値が含まれていない場合は、PCAまたはその変形の代わりにNMFを差し込むことができます。 $X$ と行列積 $WH$ との間の距離 $d$ を最適化することによって、サンプル $X$ の非負要素の2つの行列 $W$ および $H$ への分解を求める。最も広く使用されている距離関数は、ユークリッド距離の行列への明らかな拡張である、二乗Frobeniusノルムです。
d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2
PCAとは異なり、ベクトルの表現は、減算することなく成分を重ね合わせることによって、加算的に得られる。このような加法モデルは、画像およびテキストを表現するのに有効である。
[Hoyer, 04] では、注意深く拘束された場合、NMFがデータセットのパーツベースの表現を生成し、解釈可能なモデルとなることが観察されています。次の例では、Olivettiフェイスデータセットの画像から、NMAがPCA固有サーフェスと比較して見つけた16の希薄成分を表示しています。


init 属性は、適用される初期化メソッドを決定します。これは、メソッドのパフォーマンスに大きな影響を与えます。 NMFは、非負2重特異値分解法(NNDSVD) を実装しています。 NNDSVDは、データ行列に近似する2つのSVDプロセスに基づいており、結果として得られる部分SVD係数の他の近似する正のセクションは、単位ランク行列の代数的性質を利用しています。基本的なNNDSVDアルゴリズムは、疎な因子分解に適しています。 高密度の場合は、その変種NNDSVDa(すべてのゼロがデータのすべての要素の平均と等しく設定されている)とNNDSVDar(ここで、ゼロはデータの平均を100で割ったものより小さいランダムな摂動に設定される)が推奨されます。
NMFは、 init = "random" を設定することによって、正しくスケーリングされたランダムな非負行列で初期化することもできます。再現性を制御するために整数シードまたは RandomState を、 random_state に渡すこともできます。
NMFでは、モデルを正規化するために、L1関数とL2関数を損失関数に追加することができます。 L2 priorは、Frobeniusノルムを使用し、L1 priorは、要素単位L1 normを使用します。 ElasticNetのように、L1とL2の組み合わせを l1_ratio( $\rho$ )パラメータで制御し、正則化の強度を alpha( $\ alpha$ )パラメータで制御します。priors用語は次のとおりです。
\alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2
正規化された目的関数は次のとおりです。
\frac{1}{2}||X - WH||_{Fro}^2
+ \alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2
NMFはWとHの両方を正規化します。関数 non_negative_factorization は、正規化属性による細かい制御が可能で、W、Hのみ、またはその両方を正規化できます。
- 例:
- 参考文献:
- "非負行列分解による物体の部分の学習" D. Lee、S. Seung、1999
- "スパースネス制約を伴う非負行列の因子分解"P. Hoyer、2004
- "非負行列分解のための投影勾配法" C.-J. Lin、2007
- "SVDベースの初期化:非負行列分解の先頭" C. Boutsidis、E. Gallopoulos、2008
- "大規模な非負行列とテンソル分解のための高速局所アルゴリズム" A. Cichocki、P. Anh-Huy、2009
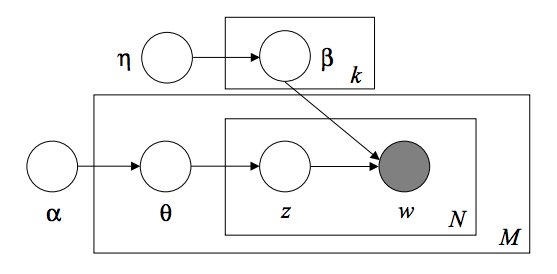
2.5.7. 潜在的ディリクレ配分法(LDA)
潜在的ディリクレ配分法(Latent Dirichlet Allocation) は、テキストコーパスなどの離散データセットを収集するための生成的確率モデルです。これは、ドキュメントの集合から抽象トピックを発見するために使用されるトピックモデルでもあります。
LDAのグラフィカルモデルは、3レベルのベイジアンモデルです。
テキストコーパスをモデリングするとき、モデルはD文書とKトピックを持つコーパスに対して次の生成プロセスを仮定します。
- 各トピック $k$ について、 $\beta_k \sim Dirichlet(\eta),: k =1...K$
- 各文書 $d$ について、 $\theta_d \sim Dirichlet(\alpha), : d=1...D$
- 文書 $d$ の各単語 $i$ について:
- トピックインデックスを描画する $z_{di} \sim Multinomial(\theta_d)$
- 観測された単語を描写する $w_{ij} \sim Multinomial(beta_{z_{di}}.)$
パラメータ推定の場合、事後分布は次のようになります。
p(z, \theta, \beta |w, \alpha, \eta) =
\frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}
後方は扱いにくいので、変分ベイズ法ではより簡単な分布を使って $q(z,\theta,\beta | \lambda, \phi, \gamma)$ を近似し、それらの変分パラメータ $\lambda, \phi, \gamma$ はEvidence Lower Bound(ELBO)を最大にするように最適化されています。
log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=}
E_{q}[log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[log\:q(z, \theta, \beta)]
ELBOを最大化することは、 $q(z,\theta,\beta)$ と真の事後 $p(z, \theta, \beta |w, \alpha, \eta)$ の間のKullback-Leibler(KL)の相違を最小化することと同等です。
LatentDirichletAllocation は、オンライン変分ベイズアルゴリズムを実装し、オンラインとバッチ更新の両方の方法をサポートします。バッチメソッドは、各フルパスをデータに渡した後に変量変数を更新しますが、オンラインメソッドでは、変分変数がミニバッチデータポイントから更新されます。
注意: オンライン方法は局所最適点に収束することが保証されていますが、最適点の品質と収束速度は、学習速度設定に関連するミニバッチサイズと属性に依存する場合があります。
LatentDirichletAllocation が "ドキュメント-用語" マトリックスに適用されると、マトリックスは "トピック-用語" マトリックスと "ドキュメント-トピック" マトリックスに分解されます。 「トピック-用語」行列はモデル中に components_ として格納されるが、 transformメソッドで "ドキュメント-トピック" 行列を計算することができる。
LatentDirichletAllocation は partial_fit メソッドも実装しています。これは、データが連続して取り出されるときに使用されます。
- 例:
- 参考文献:
- 潜在的ディリクレ配分法 D.ブレイ、A.ン、M.ジョーダン、2003年
- 潜在的ディリクレ配分法のためのオンライン学習 M.ホフマン、D.Blei、F.Bach、2010
- 確率的変分推論 M.ホフマン、D.Blei、C.Wang、J.Pasley、2013
©2010 - 2016、scikit-learn developers(BSDライセンス)。