http://scikit-learn.org/0.18/modules/density.html を google翻訳した
scikit-learn 0.18 ユーザーガイド 2. 教師なし学習 より
2.8. 密度推定
密度推定は、教師なし学習、フィーチャエンジニアリング、およびデータモデリングの間の線に沿っています。 最も一般的で有用な密度推定技術のいくつかは、ガウス混合( sklearn.mixture.GaussianMixture )のような混合モデルと、カーネル密度推定( sklearn.neighbors.KernelDensity )のような近傍ベースのアプローチです。 ガウス混合は、 クラスタ化 の文脈でより詳しく説明されています。これは、教師なしクラスタリングスキームとしても役立ちます。
密度推定は非常に単純な概念であり、ほとんどの人は既に一般的な密度推定手法であるヒストグラムに精通しています。
2.8.1. 密度推定:ヒストグラム
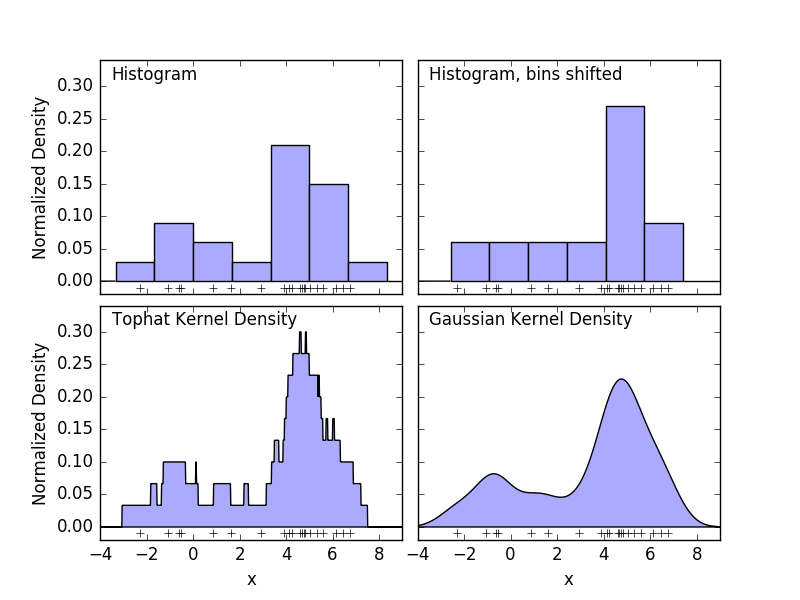
ヒストグラムは、ビンが定義されているデータの簡単なビジュアライゼーションであり、各ビン内のデータポイントの数が集計されます。ヒストグラムの例は、次の図の左上パネルに表示されます。
しかし、ヒストグラムの大きな問題は、ビニングの選択が、結果として得られる視覚化に不均衡な影響を及ぼす可能性があることです。上の図の右上のパネルを考えてみましょう。ビンを右にシフトして、同じデータのヒストグラムを表示します。2つの視覚化の結果は全く異なって見え、データの解釈が異なる場合があります。
直感的に、ヒストグラムはブロックのスタックとして、1ポイントにつき1ブロックと考えることもできます。ブロックを適切な格子空間に積み重ねることによって、ヒストグラムを回復する。しかし、通常のグリッド上にブロックを積み重ねる代わりに、各ブロックをそれが表すポイントの中心に置き、各位置の合計高さを合計するとどうなりますか?この考え方は、左下の視覚化につながります。おそらくヒストグラムほどきれいではないかもしれませんが、データがブロックの位置を駆動するという事実は、それが基になるデータをはるかに良く表現していることを意味します。
この視覚化は、カーネル密度推定の一例であり、この場合はトップハットカーネル(各点の四角形ブロック)を使用します。よりスムーズなカーネルを使用することで、よりスムーズな分布を回復することができます。右下のプロットは、ガウスカーネル密度推定値を示しています。ここで、各点は合計にガウス曲線を与えます。その結果、データから導き出された平滑な密度の推定値が得られ、点分布の強力な非パラメトリックモデルとして機能します。
2.8.2. カーネル密度推定
scikit-learnにおけるカーネル密度の推定は sklearn.neighbors.KernelDensity 推定器として実装されています。それは、効率的なクエリのためにボールツリーまたはKDツリーを使用します(これらのディスカッションについては Nearest Neighbors を参照してください)。 上記の例では単純化のために1Dデータセットを使用していますが、カーネル密度推定は任意の次元数で実行できます。しかし実際には次元の呪縛によって性能が高次元で低下します。
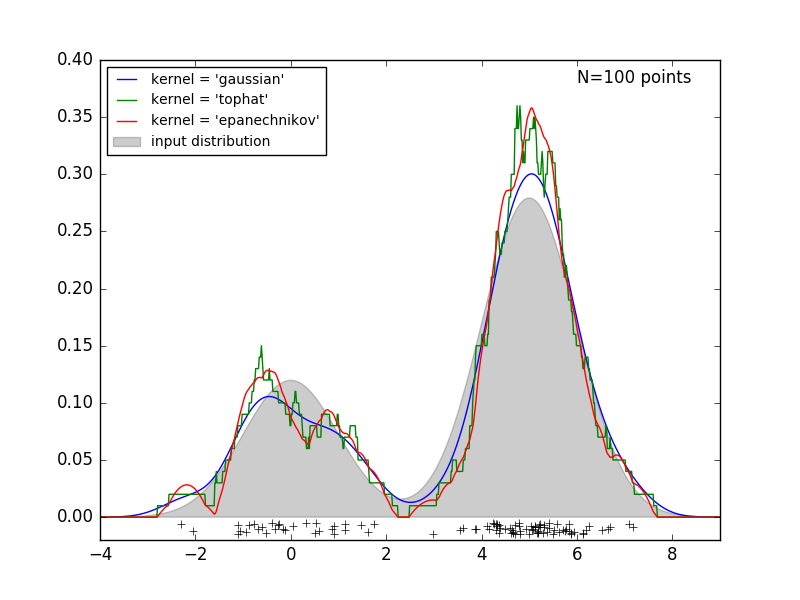
次の図では、バイモーダル分布から100点が引き出され、カーネルの3つの選択肢についてカーネル密度の推定値が示されています。
カーネルシェイプが結果として得られる分布の滑らかさにどのように影響するかは明らかです。scikit-learn カーネル密度推定器は、次のように使用できます。
>>> from sklearn.neighbors.kde import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
-0.41076071])
ここでは、上記のように kernel='gaussian' を使用しています。 数学的には、カーネルは、正の関数 $K(x;h)$ であり、これは帯域幅パラメータ $h$ によって制御される。このカーネル形式が与えられると、点群N内の点yにおける密度推定値は、次の式で与えられる。
\rho_K(y) = \sum_{i=1}^{N} K((y - x_i) / h)
ここでの帯域幅は平滑化パラメータとして作用し、結果におけるバイアスと分散との間のトレードオフを制御する。 広い帯域幅は、非常に滑らかな(すなわち、高バイアスの)密度分布をもたらす。 狭い帯域幅は、滑らかでない(すなわち、高分散)密度分布をもたらす。
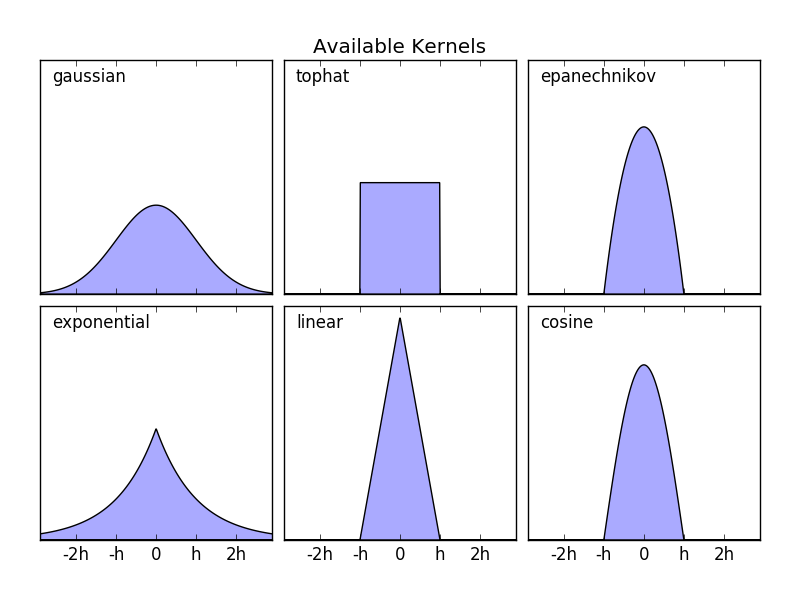
sklearn.neighbors.KernelDensity はいくつかの一般的なカーネル形式を実装しています。これを次の図に示します。
これらのカーネルの形式は次のとおりです。
- ガウスカーネル
kernel='gaussian'- $K(x; h) \propto \exp(- \frac{x^2}{2h^2} )$
- Tophatカーネル
kernel='tophat'- $K(x; h) \propto 1 if x < h$
- Epanechnikov カーネル
kernel='epanechnikov'- $K(x; h) \propto 1 - \frac{x^2}{h^2}$
- 指数関数的カーネル
kernel='exponential'- $K(x; h) \propto \exp(-x/h)$
- 線形カーネル
kernel='linear'- $K(x; h) \propto 1 - x/h if x < h$
- コサインカーネル
kernel='cosine'- $K(x; h) \propto \cos(\frac{\pi x}{2h}) if x < h$
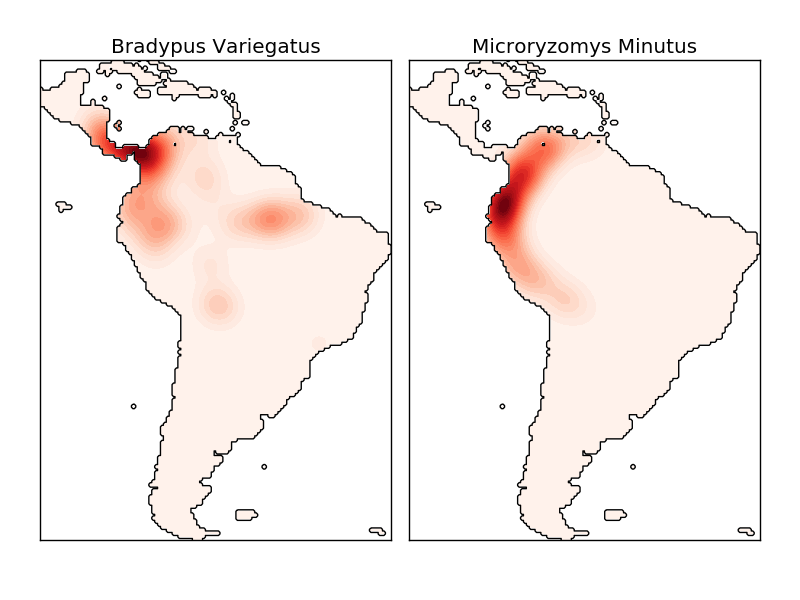
カーネル密度推定値は、有効な距離メトリック( sklearn.neighbors.DistanceMetric を参照)のどれでも使用できますが、結果はユークリッドメトリックに対してのみ適切に正規化されます。 1つの特に有用な測定基準は、球上の点間の角度距離を測定する Haversine距離 である。 地理空間データの可視化のためにカーネル密度推定を使用する例を示します。この例では、南米大陸の2つの異なる種の観測値の分布です:
カーネル密度推定の他の有用な応用例は、この生成モデルから新しいサンプルを効率的に引き出すために、データセットのノンパラメトリック生成モデルを学習することである。このプロセスを使用して、データのPCA投影で学んだガウスカーネルを使用して、手書き数字の新しいセットを作成する例を示します。
「新しい」データは入力データの線形結合で構成され、KDEモデルを仮定して確率的に描画されます。
- 例:
- 単純な1Dカーネル密度推定 :1次元における単純なカーネル密度推定値の計算。
- カーネル密度推定 :カード密度推定を使用して、手書き数字データの生成モデルを学習し、このモデルから新しいサンプルを描画する例。
- 種分布のカーネル密度推定 :地理空間データを視覚化するためのHaversine距離メトリックを用いたカーネル密度推定の一例
scikit-learn 0.18 ユーザーガイド 2. 教師なし学習 より
©2010 - 2016、scikit-learn developers(BSDライセンス)。