http://scikit-learn.org/0.18/modules/learning_curve.html を google 翻訳した
scikit-learn 0.18 ユーザーガイド 3. モデルの選択と評価 より
3.5. 検証曲線:スコアをプロットしてモデルを評価する
すべての推定値には長所と欠点があります。 その一般化誤差はバイアス、分散、ノイズの観点から分解することができます。 推定器の バイアス は、異なるトレーニングセットの平均誤差です。 推定器の 分散 は、それが変化するトレーニングセットに対してどれほど敏感であるかを示す。 ノイズはデータの特性です。
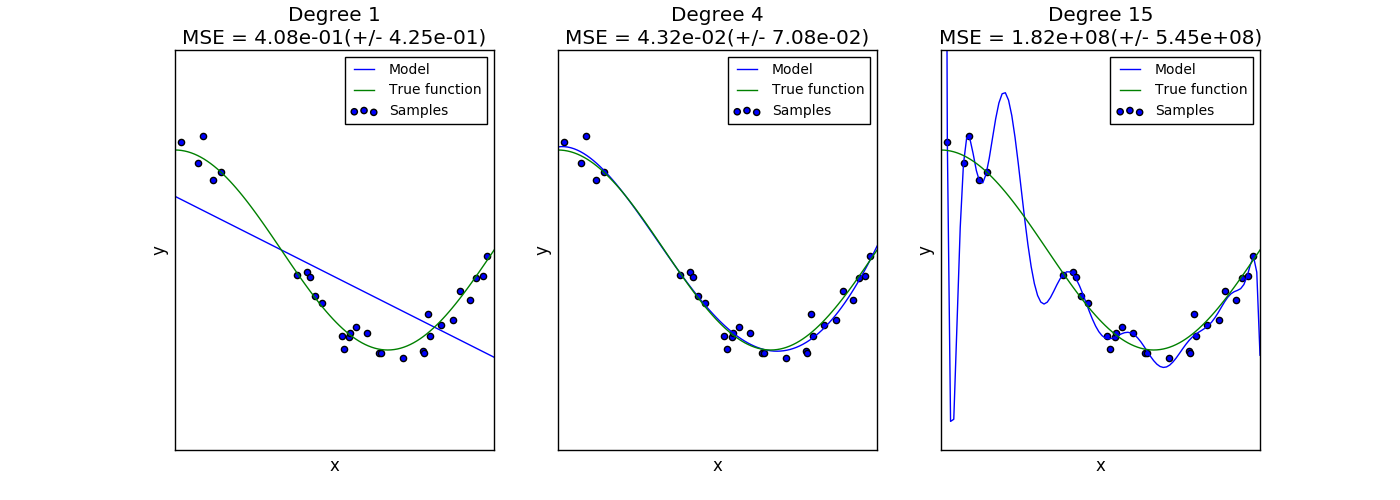
次のプロットには、関数 $f(x) = \cos (\frac{3}{2} \pi x)$ と、その関数からのノイズの多いサンプルが示されています。 我々は、次の3つの異なる評価関数をその関数に適合させるために使用します。1次、4次、15次の多項式フィーチャを使用した線形回帰。最初の推定量はあまりに単純すぎるためサンプルと実際の関数にあまり適合しないことがあります(高バイアス)。第2の推定器は、それをほぼ完全に近似する。最後の推定器は訓練データを完全に近似するが、真の関数に非常に良く適合しない。すなわち、訓練データが変化することに非常に敏感である(高分散)。
バイアスと分散は推定値の固有の特性であり、バイアスと分散の両方ができるだけ小さくなるように、通常、学習アルゴリズムとハイパーパラメータを選択する必要があります( バイアス偏差のジレンマ を参照)。モデルの分散を減らす別の方法は、より多くのトレーニングデータを使用することです。ただし、実際の関数が複雑すぎて分散が小さい推定器で近似できない場合は、さらに多くの訓練データを収集する必要があります。
この例で見たような単純な1次元問題では、推定器が偏りや分散に悩まされているかどうかを見るのは簡単です。しかし、高次元の空間では、モデルを視覚化することが非常に困難になることがあります。このため、下記のツールを使用すると便利なことがあります。
3.5.1. 検証曲線
モデルを検証するには、スコアリング関数が必要です( モデル評価:予測の品質を定量化する を参照)。たとえば、分類器の精度です。推定器の複数のハイパーパラメータを選択する適切な方法は、グリッド探索または同様の方法( 推定器のハイパーパラメータの調整 を参照)であり、検証セットまたは複数の検証セットで最大スコアを持つハイパーパラメータを選択します。検証スコアに基づいてハイパーパラメータを最適化した場合、検証スコアは偏っており、もはや一般化の良い見積もりではないことに注意してください。一般化の適切な評価を得るためには、別のテストセットでスコアを計算する必要があります。
ただし、1つのハイパーパラメータの影響を訓練スコアと検証スコアにプロットして、推定値がいくつかのハイパーパラメータ値にあまりにも適合しているか不十分であるかを調べることが役立つことがあります。
この場合、関数 validation_curve を使用すると次のようになります。
>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
... np.logspace(-7, 3, 3))
>>> train_scores
array([[ 0.94..., 0.92..., 0.92...],
[ 0.94..., 0.92..., 0.92...],
[ 0.47..., 0.45..., 0.42...]])
>>> valid_scores
array([[ 0.90..., 0.92..., 0.94...],
[ 0.90..., 0.92..., 0.94...],
[ 0.44..., 0.39..., 0.45...]])
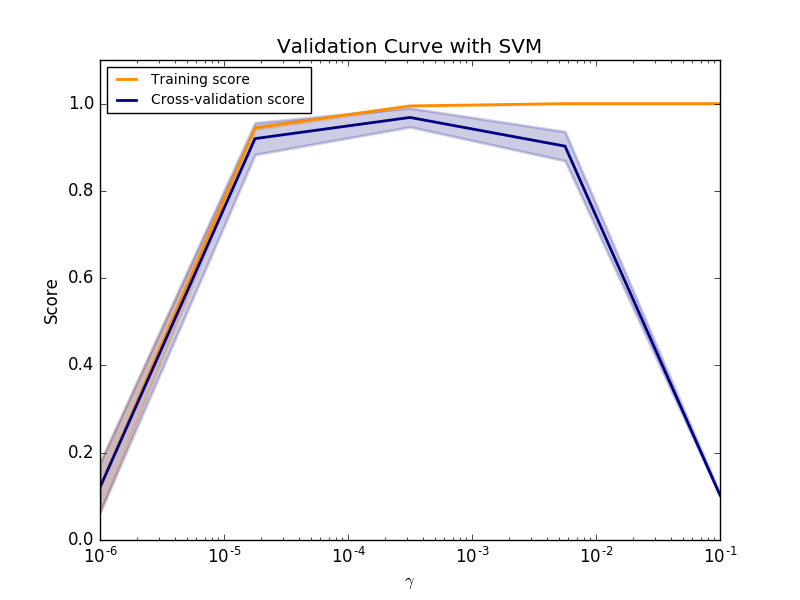
訓練スコアと検証スコアがともに低い場合、推定器はアンダーフィットです。訓練スコアが高く、検証スコアが低い場合、推定器はオーバーフィットであり、それ以外の場合は非常にうまく機能しています。低い訓練スコアと高い検証スコアは、通常ありません。 3つのケースはすべて、digitsデータセットのSVMのパラメータ $\gamma$ を変更する下のプロットで見つけることができます。
3.5.2. 学習曲線
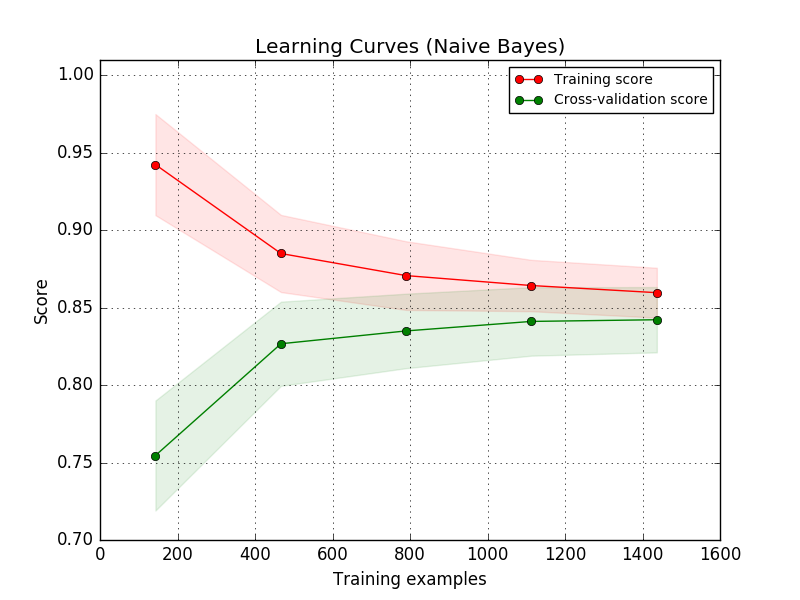
学習曲線は、様々な数の訓練サンプルに対する推定器の検証および訓練スコアを示す。これは、訓練データを追加することによってどれだけ恩恵を受けるか、また、推定器が分散誤差またはバイアス誤差によってさらに苦しんでいるかどうかを調べるためのツールです。検証スコアと訓練スコアの両方が、訓練セットのサイズが大きくなるにつれて低すぎる値に収束した場合、訓練データを増やしても利益を得ることはできない。以下のプロットで例を見ることができます。ネイティブベイズは、概して低いスコアに収束します。
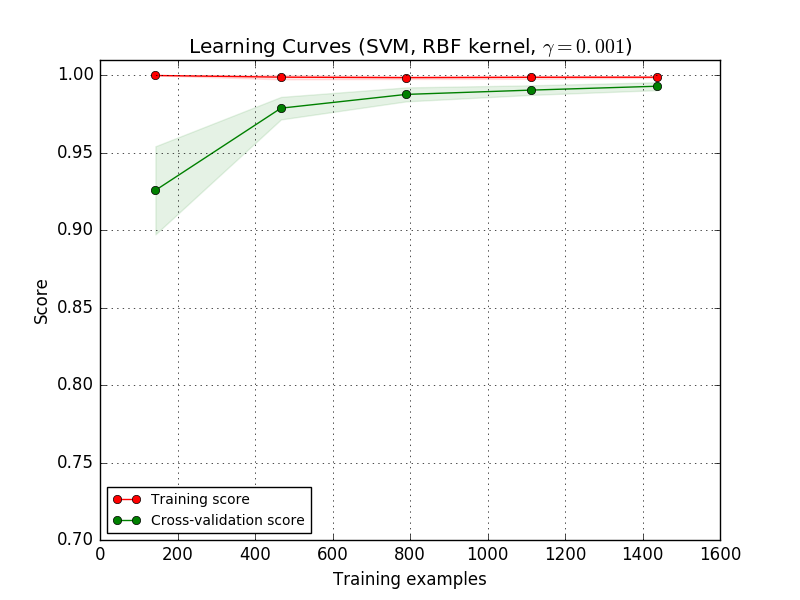
おそらく、より複雑な概念を学ぶことができる(すなわち、よりバイアスが低い)推定器または現在の推定器のパラメータ化を使用しなければならない。 訓練スコアが訓練サンプルの最大数に対する検証スコアよりもはるかに大きい場合、訓練サンプルを追加することは、一般化を増加させる可能性が最も高い。 以下のプロットでは、SVMがより多くの訓練例の恩恵を受けることが分かります。
learning_curve 関数を使用して、このような学習曲線(使用されたサンプルの数、訓練セットの平均スコア、および検証セットの平均スコア)をプロットするために必要な値を生成することができます。
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[ 0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[ 0.98..., 1. , 0.98..., 0.98..., 0.98...],
[ 0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[ 1. , 0.93..., 1. , 1. , 0.96...],
[ 1. , 0.96..., 1. , 1. , 0.96...],
[ 1. , 0.96..., 1. , 1. , 0.96...]])
scikit-learn 0.18 ユーザーガイド 3. モデルの選択と評価 より
©2010 - 2016、scikit-learn developers(BSDライセンス)。