http://scikit-learn.org/0.18/modules/calibration.html を google 翻訳した
scikit-learn 0.18 ユーザーガイド 1. 教師付き学習 より
1.16. 確率較正
分類を実行するときには、クラスラベルを予測するだけでなく、それぞれのラベルの確率を得ることがしばしばあります。 この確率は、予測に対して何らかの信頼を与えます。 モデルによっては、クラス確率の見積もりが悪いものもあれば、確率予測をサポートしていないモデルもあります。 較正モジュールを使用すると、特定のモデルの確率をより適切に調整したり、確率予測のサポートを追加したりすることができます。
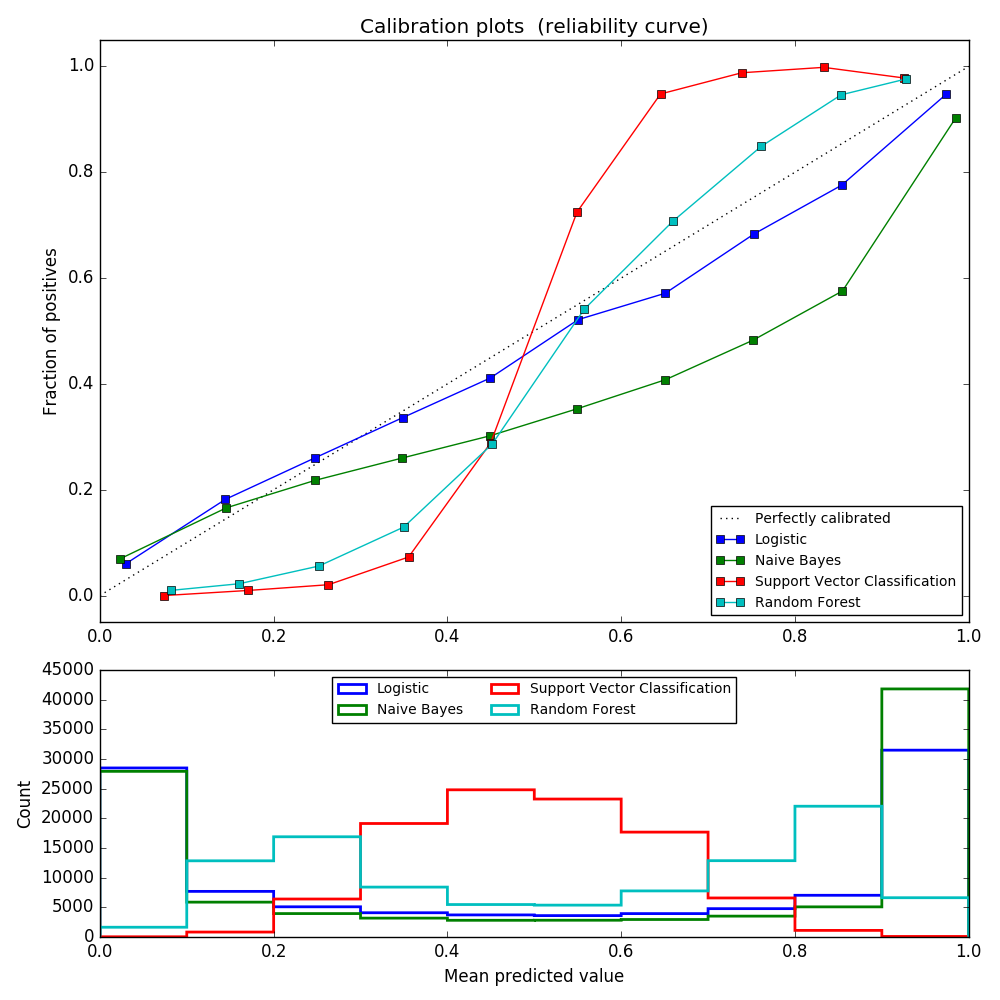
よく較正された分類器は、predict_probaメソッドの出力を信頼水準として直接解釈できる確率的分類器である。 例えば、よく較正された(バイナリ)分類器が 0.8 の predict_proba 値を与えたサンプルは、約80%が実際に陽性クラスに属する。 次のプロットは、さまざまな分類器の確率的予測がどの程度うまく較正されているかを比較しています。
LogisticRegression は、ログ損失を直接最適化するため、デフォルトで適切に較正された予測を返します。対照的に、他の方法は偏った確率を返す。メソッドごとに異なる偏りを持つ:
- GaussianNB は確率を0または1に押し出す傾向があります(ヒストグラムの数に注意してください)。これは、クラスが与えられたときに特徴量が条件付きで独立しているという前提があるためです。2つの冗長特徴量を含むこのデータセットの場合には当てはまらない。
- RandomForestClassifier は反対の振る舞いを示します。ヒストグラムは約0.2と0.9の確率でピークを示し、0または1に近い確率は非常にまれです。これについての説明は、Niculescu-Mizil and Caruana [4]によって行われています。「バギングやランダムフォレストなど、モデルの基本セットからの予測を平均化する方法では、基礎となるベースモデルの分散がこれらの値から0または1に近づくはずの予測をバイアスするため、0および1に近い予測を行うことが困難になります。予測は区間[0,1]に制限されるため、分散に起因する誤差は0と1に近い片側になる傾向があります。たとえば、モデルがケースに対してp = 0を予測する必要がある場合、バギングがこれを達成する唯一の方法は、すべてのバグ付きツリーがゼロを予測することです。バギングが平均化されているツリーにノイズを追加すると、このノイズによって、このケースでは0より大きい値を予測するツリーが生成され、バックグラウンドアンサンブルの平均予測が0から離れることになります。ランダムフォレストで訓練されたベースレベルのツリーは、特徴量サブセット化のため比較的分散が大きいため、この効果はランダムフォレストで最も強く観察されます」。結果として、較正曲線は特徴的なシグモイド形状を示し、分類器がその「直観」をより信頼し、一般的に0または1に近い確率を返すことができることを示している。
- 線形サポートベクトル分類( LinearSVC )は、RandomForestClassifierとしてより大きなシグモイド曲線を示します。これは、決定境界に近いハードサンプルに焦点を当てた最大マージン法(Niculescu-MizilとCaruana [4]と比較して)では一般的です。
確率的予測の較正を実行するための2つのアプローチ、すなわち、プラットのシグモイドモデルに基づくパラメトリックアプローチおよびアイソトニック回帰( sklearn.isotonic )に基づくノンパラメトリックアプローチが提供される。 モデルフィッティングに使用されない新しいデータに対して確率較正を実行する必要があります。 CalibratedClassifierCV クラスは、クロスバリデーションジェネレータを使用して、訓練サンプル上のモデルパラメータとテストサンプルのキャリブレーションの各スプリットを推定します。 次に、fold のために予測される確率が平均化される。 既に適合している分類器は、パラメータ cv="prefit" を介して CalibratedClassifierCV によって較正することができます。 この場合、モデルのフィッティングと較正のためのデータが不連続であることをユーザが手動で注意しなければならない。
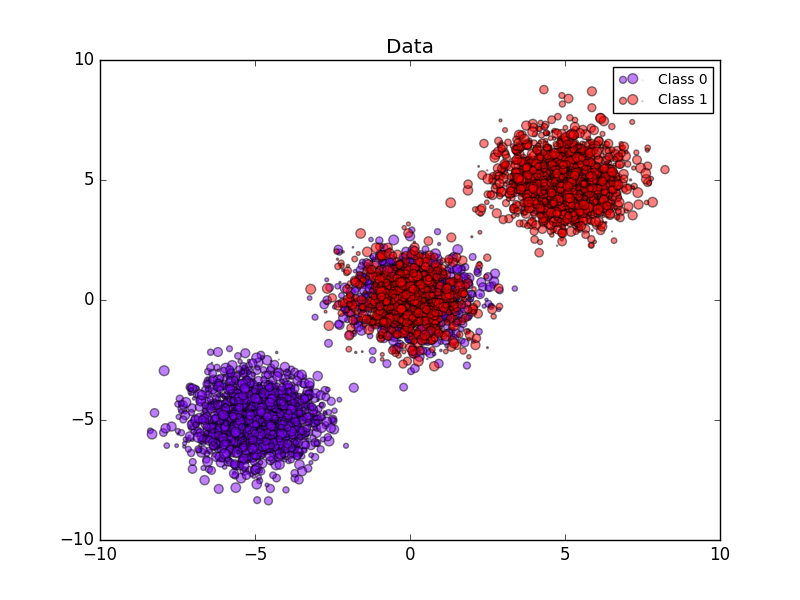
次の画像は確率較正の利点を示しています。最初の画像は、データセットの2つのクラスと3つの塊を表します。中央の塊には、各クラスのランダムサンプルが含まれています。この塊のサンプルの確率は0.5でなければなりません。
次の画像は、校正なしのガウス型ナイーブベイズ分類器、シグモイド校正、およびノンパラメトリックアイソトニック校正を使用して、推定確率より上のデータを示しています。ノンパラメトリックモデルは、中央のサンプルについて最も正確な確率推定値、すなわち0.5を提供することを観察することができる。
次の実験は、20個の特徴量を有する100.000個のサンプル(モデルフィッティングに1.000個のサンプルが使用される)を有するバイナリ分類のための人工データセットに対して実施される。 20の特徴量のうち、2つだけが有益であり、10は冗長です。この図は、ロジスティック回帰、線形サポートベクトル分類器(SVC)、およびアイソトニック較正およびシグモイド較正の両方を有する線形SVCで得られた推定確率を示す。校正性能は、Brierスコア brier_score_loss で評価され、凡例で報告されます(小さい方が良い)。
ここで、ロジスティック回帰は、その曲線がほぼ対角であるため、較正されていることが分かります。線形SVCの検量線にはシグモイド曲線があり、これは「自信のある」分類器に特有のものです。 LinearSVCの場合、これはヒンジ損失のmarginプロパティによって引き起こされます。これにより、モデルは決定境界に近いハードサンプル(サポートベクトル)に焦点を合わせることができます。両方の種類のキャリブレーションでこの問題が解決され、ほぼ同じ結果が得られます。次の図は、両方の種類のキャリブレーションとキャリブレーションなしで、同じデータ上のガウス・ナイーブベイズのキャリブレーション曲線を示しています。
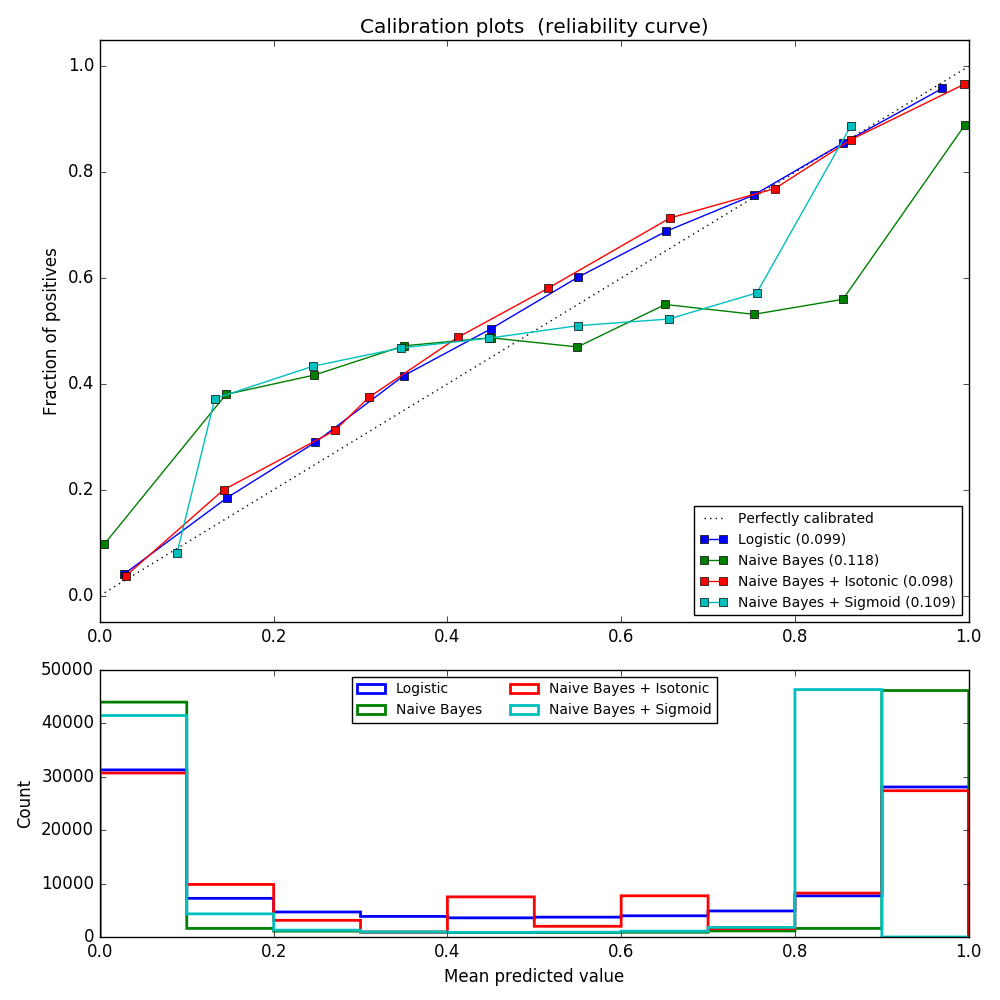
Gaussian naive Bayesは非常に悪い結果を出すが、リニアSVC以外の方法で実行されることがわかる。 線形SVCはシグモイド較正曲線を示したが、ガウス式ナイーブベイズ較正曲線は、転置されたシグモイド形状を有する。 これは、楽観的すぎる分類器では一般的です。 この場合、分類器の過信は、特徴量非依存性のナイーブベイズ仮定に違反する冗長な特徴量によって引き起こされます。
ほぼ対角の較正曲線から分かるように、Gaussian naive Bayesのアイソトニック回帰確率較正はこの問題を修正することができる。シグモイド較正はまた、非パラメトリックアイソトニック較正ほど強力ではないが、brierスコアをわずかに改善する。これは、シグモイド較正の本質的な制限であり、そのパラメトリック形式は、転置されたシグモイド曲線ではなくシグモイドを仮定している。しかし、ノンパラメトリックなアイソトニック較正モデルは、そのような強い仮定を立てておらず、十分な較正データがあれば、いずれの形状にも対処することができる。一般に、較正曲線がシグモイドであり、較正データが限られている場合には、シグモイド較正が好ましいが、非シグモイド較正曲線および較正のために大量のデータが利用可能な状況では、アイソトニック較正が好ましい。
CalibratedClassifierCV は、ベース推定がそうすることができる場合、2つ以上のクラスを含む分類タスクも処理できます。この場合、分類器は、各クラスに対して1対1の別の方法で個別に較正される。見えないデータの確率を予測する場合、各クラスの較正された確率は別々に予測される。それらの確率は必ずしも1に合わないので、事後処理を行ってそれらを正規化する。
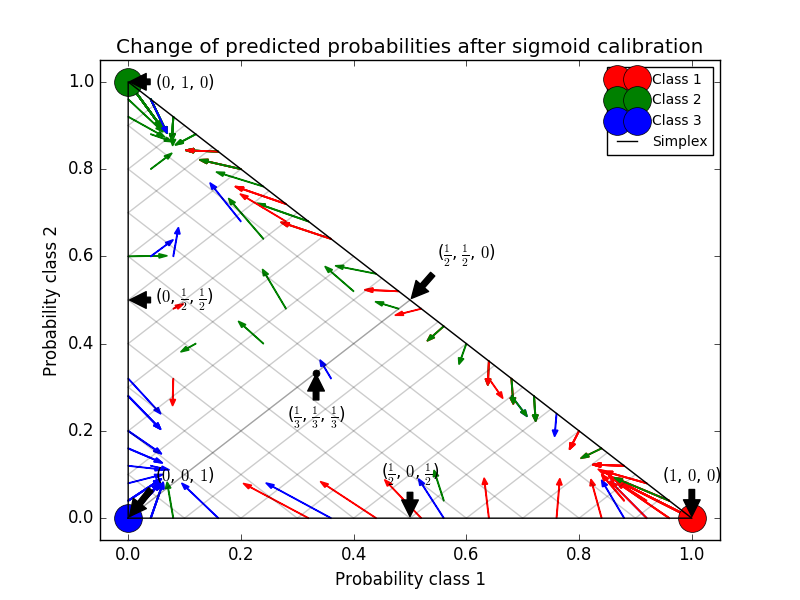
次の画像は、シグモイド較正が3クラス分類問題の予測確率をどのように変化させるかを示しています。 3つのコーナーが3つのクラスに対応する標準の2シンプレックスが例示されている。矢印は、較正されていない分類器によって予測された確率ベクトルから、ホールドアウト検証セットのシグモイド較正の後に同じ分類器によって予測された確率ベクトルを指す。色はインスタンスの真のクラスを示します(赤:クラス1、緑:クラス2、青:クラス3)。
ベース分類器は、25個のベース推定器(ツリー)を有するランダムフォレスト分類器である。この分類器がすべての800のトレーニングデータポイントで訓練されている場合、その予測には過度の自信があり、大きなログ損失が発生します。残りの200個のデータポイント上で、600個のデータポイントで訓練された同一の分類器を method='sigmoid' で較正することは、予測の信頼性を低下させる、すなわち、シンプレックスのエッジから中心に向かって確率ベクトルを移動させる。
この較正は、より低い対数損失をもたらす。代替案は、対数損失の同様の減少をもたらすであろうベース推定量の数を増加させることであったことに留意されたい。
- 参考文献:
- [1]決定木とナイーブベイズ分類器から較正された確率推定値を得る、B. Zadrozny&C. Elkan、ICML 2001
- [2]クラシファイアスコアを正確なマルチクラス確率推定に変換する、B. Zadrozny&C. Elkan、(KDD 2002)
- [3]サポートベクトルマシンの確率的出力と正規化された尤度法との比較、J. Platt、(1999)
- [4]教師付き学習による良い確率の予測、A. Niculescu-Mizil&R. Caruana、ICML 2005
scikit-learn 0.18 ユーザーガイド 1. 教師付き学習 より
©2010 - 2016、scikit-learn developers(BSDライセンス)。