http://scikit-learn.org/0.18/modules/ensemble.html を google翻訳した
scikit-learn 0.18 ユーザーガイド 1. 教師付き学習 より
1.11. アンサンブルメソッド
アンサンブル学習 の目標は、単一の推定器に対する汎用性/頑健性を向上させるために、与えられた学習アルゴリズムで構築されたいくつかの基本推定器の予測を組み合わせることです。
通常、アンサンブル学習は2つのファミリに区別されます。
-
平均化手法 は、いくつかの推定器を独立して作成し、それらの予測値を平均化することを原則としています。 平均して、結合された推定器は、その分散が減少するので、通常、単一の推定器よりも優れている。
- 例:バギング法、無作為化された木の森、...
-
対照的に、 ブースティング法 では、ベース推定器が順次構築され、結合推定器のバイアスを低減しようとする。 モチベーションはいくつかの弱いモデルを組み合わせて強力なアンサンブルを作り出すことです。
- 例:AdaBoost、勾配ツリーブースト、...
1.11.1. バギング メタ推定器
アンサンブルアルゴリズムでは、バギング法は、元のトレーニングセットのランダムなサブセットにブラックボックス推定器を構築し、個々の予測を集約して最終的な予測を形成する、アルゴリズムのクラスを形成します。これらの方法は、ランダム化をその構築手順に導入し、アンサンブルを作成することによって、ベース推定器(例えば、決定木)の分散を低減します。多くの場合、バギング法は、基礎となる基本アルゴリズムを適応させる必要なく、単一のモデルに関して改善する非常に簡単な方法を構成します。それらが過剰適合を減らす方法を提供するので、通常、弱いモデル(例えば、浅い決定木)で最も効果的なブースティング方法とは対照的に、バギング法は強くて複雑なモデル(例えば、完全に展開された決定木)で最も効果的である。
バギング法は多くの種類がありますが、トレーニングセットのランダムな部分集合を描く方法による違いがほとんどです。
- データセットのランダムなサブセットがサンプルのランダムなサブセットとして描かれるとき、このアルゴリズムは Pasting と呼ばれます。[B1999]
- サンプルを置き換えて描画する場合、この方法は Bagging として知られています。[B1996]
- データセットのランダムな部分集合が特徴量のランダムな部分集合として描かれるとき、その方法はランダムな部分空間として知られている。[H1998]
- 最後に、ベース推定器がサンプルと特徴量の両方のサブセット上に構築される場合、この方法はランダムパッチとして知られている。[LG2012]
scikit-learnでは、バギング法は、 BaggingClassifier メタ推定器(及び BaggingRegressor )として提供され、ランダムサブセットを描画するための戦略を指定するパラメータと共にユーザ指定のベース推定器を入力として受け取ります。特に、 max_samples と max_features はサブセットのサイズを(サンプルと特徴量の観点から)制御しますが、 bootstrap と bootstrap_features はサンプルと特徴量を置き換えるかどうかを制御します。使用可能なサンプルのサブセットを使用する場合、 oob_score = True を設定することにより、アウトオブバッグサンプルで一般化の精度を推定することができます。例として、以下のスニペットは、サンプルの50%と特徴量の50%のランダムなサブセットで構築された KNeighborsClassifier ベースの特徴器値のバギングアンサンブルをインスタンス化する方法を示します。
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5, max_features=0.5)
-
例:
-
参考文献
- [B1999] L. Breiman、 "大きなデータベースとオンラインで分類するために小さな票を貼る"機械学習、36(1)、85-103、1999
- [B1996] L. Breiman、 "Bagging predictors"、機械学習、24(2)、123-140、1996
[H1998] T. Ho、「決定フォレストを構築するためのランダム部分空間法」、パターン解析と機械知能、20(8)、832-844、1998。 - [LG2012] G. LouppeとP. Geurts、「無作為パッチに関するアンサンブル」、データベースにおける機械学習と知識発見、346-361、2012。
1.11.2. ランダム化された木の森
sklearn.ensemble モジュールには、RandomForestアルゴリズムとExtra-Treesメソッドというランダム化された決定木に基づく2つの平均化アルゴリズムが含まれています。 両方のアルゴリズムは、樹木のために特別に設計された摂動と結合技術 [B1998] です。 これは、分類器構築にランダム性を導入することによって、多様な分類器セットが作成されることを意味する。 アンサンブルの予測は、個々の分類器の平均予測として与えられる。
他の分類器として、フォレスト分類器には2つの配列が必要です。トレーニングサンプルを保持するサイズ [n_samples, n_features] のスパースまたは密な配列Xと、ターゲット値(クラスラベル)を保持するサイズ [n_samples] の配列Y トレーニングサンプル:
>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)
決定木 と同様に、ツリーの森は マルチ出力問題 にも拡張されます(Yがサイズ [n_samples, n_outputs] の配列の場合)。
1.11.2.1. ランダムフォレスト
ランダムフォレスト( RandomForestClassifier クラスと RandomForestRegressor クラスを参照)では、アンサンブルの各ツリーは、トレーニングセットの置換(すなわち、ブートストラップサンプル)で描画されたサンプルから構築されます。さらに、ツリーの構築中にノードを分割する場合、選択された分割は、もはやすべての特徴量の中で最良の分割ではなくなりました。代わりに、ピックされた分割は、特徴量のランダムなサブセットの中で最も良い分割です。このランダム性の結果として、森林の偏りは、通常、(単一の非ランダム木の偏りに関して)わずかに増加するが、平均化のために、その偏差も減少し、通常はバイアスの増加を補うだけでなく、全体としてより良いモデルが得られます。
元の論文 [B2001] とは対照的に、scikit-learnの実装は、各分類器に単一のクラスに投票させる代わりに、確率的予測を平均化することによって分類器を組み合わせる。
1.11.2.2. 非常にランダム化された木
非常にランダム化されたツリー( ExtraTreesClassifier クラスと ExtraTreesRegressor クラスを参照)では、分割が計算される方法において、ランダム性はさらに一歩進んでいます。ランダムフォレストの場合と同様に、候補特徴量のランダムなサブセットが使用されますが、最も顕著なしきい値を探す代わりに、候補特徴量ごとにランダムにしきい値が描画され、これらのランダムに生成されたしきい値の最高値が分割ルールとして選択されます。これは、通常、バイアスのわずかな増加を犠牲にして、モデルの分散をさらに少しだけ減らすことを可能にします。
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
... random_state=0)
>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
... random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.97...
>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.999...
>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean() > 0.999
True
1.11.2.3. パラメーター
これらのメソッドを使用するときに調整する主なパラメータは n_estimators と max_features です。前者は木の数です。大きい方が良いですが、計算に時間がかかります。さらに、重要な数のツリーを超えても結果が大幅に改善されないことに注意してください。後者は、ノードを分割するときに考慮すべき特徴量のランダムなサブセットのサイズです。低いほど、分散の減少は大きくなるが、バイアスの増加も大きくなる。経験的に良いデフォルト値は、回帰問題の場合は max_features = n_features 、分類タスクの場合は max_features = sqrt(n_features) です( n_features はデータ内の特徴量の数です)。 max_depth = None を min_samples_split = 1(すなわち、ツリーを完全に展開するとき)と組み合わせて設定すると、良い結果が得られることが多い。しかし、これらの値は通常最適ではなく、多くのRAMを消費するモデルになる可能性があることに注意してください。最良のパラメータ値は常にクロスバリデーションされるべきです。さらに、ランダムフォレストでは、デフォルトでブートストラップサンプルが使用され( bootstrap = True )、エクストラツリーのデフォルト戦略はデータセット全体を使用する( bootstrap = False )ことに注意してください。ブートストラップサンプリングを使用するとき、一般化の精度は、レフトアウトまたはアウトオブバッグサンプルで推定することができます。これを有効にするには、 oob_score = True を設定します。
1.11.2.4. 並列化
最後に、このモジュールはツリーの並列構造と、 n_jobs パラメータによる予測の並列計算も特長としています。 n_jobs = k の場合、計算は k 個のジョブに分割され、マシンの k 個のコアで実行されます。 n_jobs = -1 の場合、マシン上で使用可能なすべてのコアが使用されます。プロセス間通信オーバヘッドのために、スピードアップは線形ではないかもしれない(すなわち、 k ジョブを使用することは残念ながら k 倍高速ではない)。多数の木を構築するときや、単一の木を構築するときにかなりの時間(例えば、大規模なデータセット)を必要とするときでさえも、大幅なスピードアップを達成することができる。
-
例:
-
参考文献
- [B2001] Breiman、 "ランダムフォレスト"、機械学習、45(1)、5-32,2001。
- [B1998] Breiman、 "Arcing Classifiers"、Annals of Statistics 1998
- [GEW2006] P. Geurts、D. Ernst。、およびL. Wehenkel、「超無作為化された木」、Machine Learning、63(1)、3-42,2006。
1.11.2.5. 特徴量の重要度評価
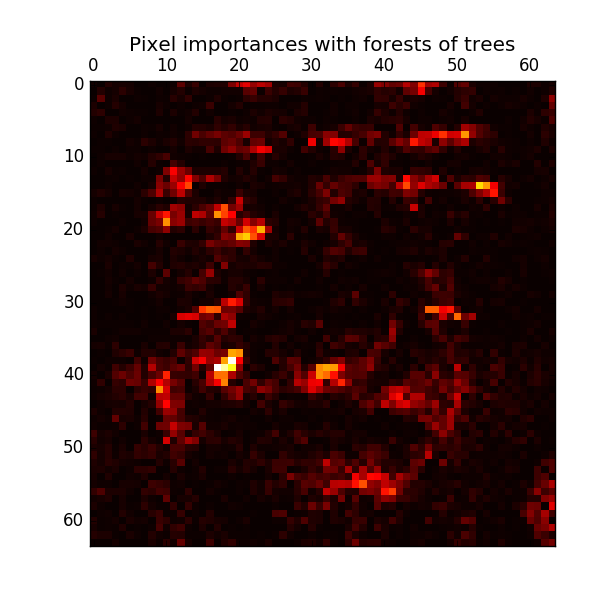
ツリー内の決定ノードとして使用される特徴量の相対的ランク(すなわち深さ)を使用して、ターゲット変数の予測可能性に関するその特徴量の相対的重要度を評価することができる。木の頂部で使用される特徴量は、入力サンプルのより大きな部分の最終的な予測決定に寄与する。したがって、 それらが寄与するサンプルの期待される割合 は、 特徴量(説明変数)の相対的重要度 の推定値として使用することができる。
いくつかの無作為化された樹木にわたってこれらの期待された活動率を 平均化 することにより、そのような推定値の 分散を減少 させ、それを特徴量選択に使用することができる。
次の例は、 ExtraTreesClassifier モデルを使用した顔認識タスクの各ピクセルの相対的な読み込みの色分けされた表現を示しています。
実際には、これらの推定値はフィッティングされたモデルに feature_importances_ という名前の属性として保存されます。これはシェイプ (n_features, ) の値が正の値で1.0の合計を持つ配列です。値が高いほど、一致関数の予測関数への寄与がより重要になります。
1.11.2.6. 完全にランダムなツリー埋め込み
RandomTreesEmbedding は、教師なしのデータ変換を実装します。完全にランダムなツリーのフォレストを使用して、 RandomTreesEmbedding は、データポイントが終わるリーフのインデックスによってデータをエンコードします。このインデックスは、Kの1対1の方法でエンコードされ、高次元の疎なバイナリコーディングにつながります。このコーディングは非常に効率的に計算され、他の学習タスクの基礎として使用できます。コードのサイズと希薄さは、ツリーの数とツリーあたりの最大深さを選択することによって影響を受ける可能性があります。アンサンブル内の各ツリーに対して、コーディングには1つのエントリが含まれます。コーディングのサイズは最大で n_estimators * 2 ** max_depth 、フォレスト内の最大葉数です。
隣接するデータポイントがツリーの同じリーフ内にある可能性が高いので、変換は暗黙の非パラメトリック密度推定を実行する。
- 例:
- 完全無作為木を使ったハッシュ変換
- 手書き数字のマニホールド学習:局所的線形埋め込み、Isomap... は手書き数字の非線形次元削減技術を比較します。
- ツリーのアンサンブルによる特徴量変換 は、監督されたツリーと管理されていないツリーベースの特徴量変換を比較します。
See also: マニホールド学習 技術は、特徴量空間の非線形表現を導出するのにも役立ちます。また、これらのアプローチは次元削減にも重点を置いています。
1.11.3. AdaBoost
モジュール sklearn.ensemble には、Freund と Schapire によって1995年に導入された一般的なブースティングアルゴリズム AdaBoost [FS1995] が含まれています。
AdaBoost のコア原則は、繰り返し修正されたバージョンのデータに対して、弱学習器のシーケンス(小さな決定木など、ランダムな推測よりわずかに優れたモデル)を適合させることです。それらのすべてからの予測は、最終的な予測を生成するために重み付けされた多数決(または合計)によって結合されます。各ブースティング反復におけるデータ修正は、トレーニングサンプルのそれぞれに重み $w_1, w_2, ..., w_N$ を適用することからなる。最初は、これらの重みはすべて $w_i = 1 / N$ に設定されているため、最初のステップでは弱学習器に元のデータを単純に訓練します。反復ごとに、サンプルの重みが個別に変更され、学習アルゴリズムが再加重されたデータに再適用されます。与えられたステップでは、前のステップで誘発されたブーストされたモデルによって誤って予測されたトレーニング例は、重みが増加し、正しく予測されたものに対しては、重みが減少する。反復が進むにつれて、予測が困難な例はますます増加する影響を受ける。その後の各弱学習器は、シーケンスの前の弱学習器が見逃した例に集中することを余儀なくされる [HTF]。
- AdaBoostは、分類問題と回帰問題の両方に使用できます。
- マルチクラス分類では、AdaBoost-SAMMEとAdaBoost-SAMME.R [ZZRH2009]を実装した AdaBoostClassifier を。
- 回帰の場合、AdaBoost.R2 [D1997] を実装した AdaBoostRegressor を。
1.11.3.1. 使用法
次の例は、AdaBoost分類器で 100の弱学習器を用いて学習する方法を示しています。
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> iris = load_iris()
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, iris.data, iris.target)
>>> scores.mean()
0.9...
弱学習器の数は、パラメータ n_estimators によって制御されます。 learning_rate パラメータは、最終的な組み合わせにおける弱学習器の寄与を制御します。デフォルトでは、弱学習器は 決定株 です。 base_estimator パラメータを使用して、弱学習器を指定することができます。良好な結果を得るために調整する主なパラメータは、 n_estimator と、ベース推定値の複雑さ(例えば、デプスツリーの場合、デプス max_depth またはリーフ min_samples_leaf でのサンプルの最小必要数)です。
-
例:
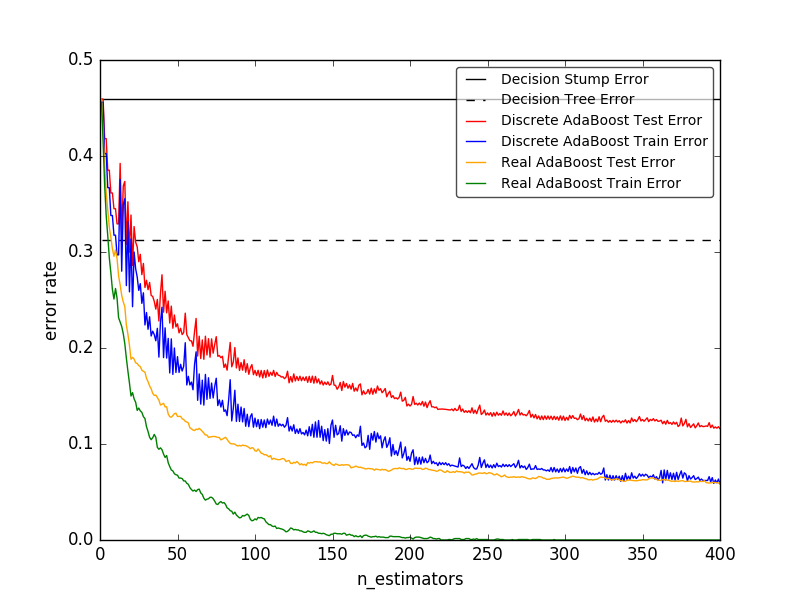
- 離散対実数AdaBoost は、AdaBoost-SAMMEとAdaBoost-SAMME.Rを使用して、決定断端、決定木、およびブーストされた決定断端の分類誤差を比較します。
- マルチクラスのAdaBoosted Decision Trees は、マルチクラスの問題に対するAdaBoost-SAMMEとAdaBoost-SAMME.Rのパフォーマンスを示します。
- 2クラスのAdaBoost は、AdaBoost-SAMMEを使用して、非線形に分離可能な2クラス問題の決定境界値と決定関数値を示します。
- AdaBoostによるDecision Tree Regression は、AdaBoost.R2アルゴリズムによる回帰を示します。
-
参考文献
- [FS1995] Y. FreundとR. Schapire、 "オンライン学習の決定論的一般化とブースティングへの応用"、1997。
- [ZZRH2009] J. Zhu、H.Zou、S.Rosset、T.Hastie。 "マルチクラスAdaBoost"、2009。
- [D1997] ドラッカー。 "ブースティング技術を用いた回帰機の改良"、1997。
- [HTF] T. Hastie、R. TibshiraniおよびJ. Friedman、 "Elements of Statistical Learning Ed。 2 "、Springer、2009。
1.11.4. 勾配ツリーブースト
勾配ツリーブースト または勾配ブースト回帰ツリー(GBRT)は、任意の微分可能な損失関数にブーストする一般化です。 GBRTは、回帰および分類問題の両方に使用できる、正確で効果的な市販の手順です。 Gradient Tree Boostingモデルは、Web検索ランキングや生態学など、さまざまな分野で使用されています。
- GBRTの利点は次のとおりです。
- 混合型データ(=異質な特徴量)の自然な扱い
- 予測力
- 出力空間における異常値に対するロバスト性(ロバストなロス関数による)
- GBRTの欠点は次のとおりです。
- ブースティングのシーケンシャル性のためほとんど並列化できません。
モジュール sklearn.ensemble は、勾配ブーストされた回帰木による分類と回帰の両方のためのメソッドを提供します。
1.11.4.1. 分類
GradientBoostingClassifier は、バイナリクラスとマルチクラスの両方の分類をサポートします。次の例は、勾配ブースティング分類器を100人の決定株と弱学習器として適合させる方法を示しています。
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...
弱学習器(すなわち、回帰木)の数は、パラメータ n_estimators によって制御される。 各ツリーのサイズ は、ツリーの深さを max_depth で設定するか、 max_leaf_nodes でリーフノードの数を設定することによって制御できます。 learning_rate は、 収縮 によるオーバーフィットを制御する範囲 (0.0, 1.0] のハイパーパラメータです。
注意: 2つ以上のクラスを持つ分類は、各反復で n_classes 回帰木の誘導を必要とするため、誘導木の総数は n_classes * n_estimators に等しくなります。 多数のクラスを持つデータセットの場合、 GradientBoostingClassifier の代わりに RandomForestClassifier を使用することを強くお勧めします。
1.11.4.2. 回帰
GradientBoostingRegressor は、引数の loss によって指定できる回帰のさまざまな 損失関数 をサポートしています。 回帰のデフォルト損失関数は最小二乗( 'ls' )です。
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
... max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00...
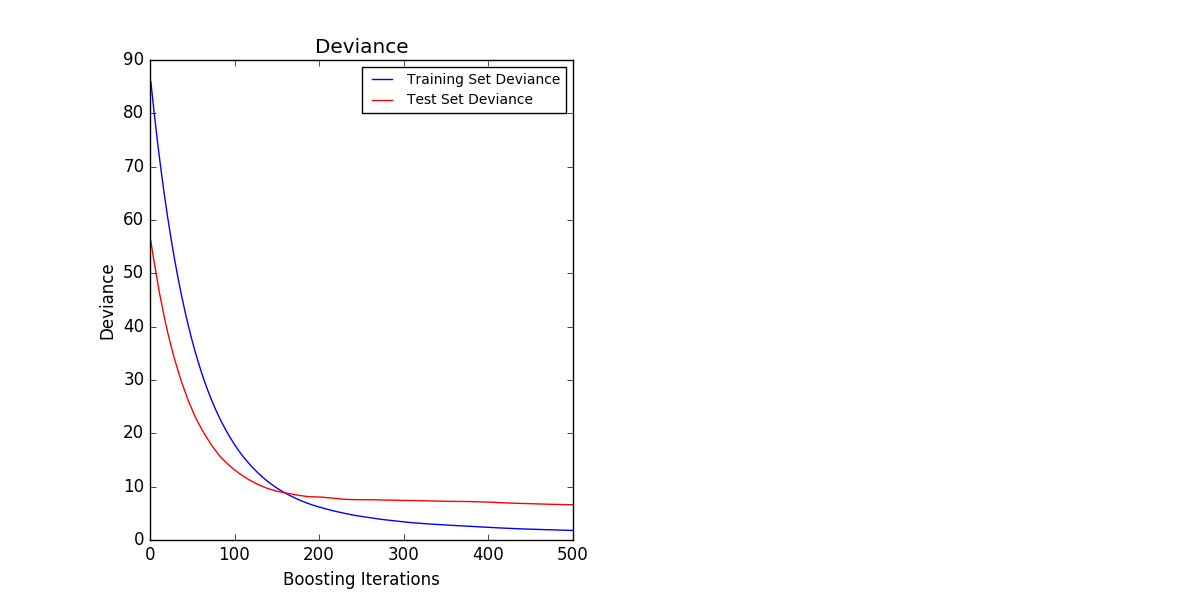
下の図は、ボストンの住宅価格データセット( sklearn.datasets.load_boston )に対して、最小二乗損失および500ベースの学習者が適用された GradientBoostingRegressor の結果を示しています。 左のプロットは列車と各反復時のテストエラーを示しています。 各反復における列車誤差は、勾配ブースティングモデルの train_score_ 属性に格納されます。 各反復でのテストエラーは、ステージごとに予測を生成するジェネレータを返す staged_predict メソッドを使用して取得できます。 このようなプロットを使用して、早期停止によって最適なツリー数( n_estimators )を決定することができます。 右側のプロットは、 feature_importances_ プロパティを使用して取得できる特徴量のインポートを示しています。
1.11.4.3. 追加の学習
GradientBoostingRegressor と GradientBoostingClassifier はどちらも、 warm_start = True をサポートしています。これにより、既に fit したモデルに学習を追加できます。
>>> _ = est.set_params(n_estimators=200, warm_start=True) # set warm_start and new nr of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84...
1.11.4.4. ツリーサイズの制御
回帰木ベース学修器のサイズは、勾配ブースティングモデルによって取り込まれる可変相互作用のレベルを定義します。一般に、深さ h の木は、次数 h の相互作用を捕捉することができる。個々の回帰木のサイズを制御するには2つの方法があります。
max_depth = h を指定すると、深さ h のバイナリツリーが完成します。そのような木は、(最大で)2 ** h の葉ノードと 2 ** h-1 の分割ノードを有する。
または、 max_leaf_nodes パラメータを使用してリーフノードの数を指定してツリーサイズを制御することもできます。この場合、不純物が最も改善されたノードが最初に展開されるベストファーストサーチを使用してツリーが成長します。 max_leaf_nodes = k のツリーは、 k-1 個の分割ノードを持ち、 max_leaf_nodes-1 までの相互作用をモデル化することができます。
我々は、 max_leaf_nodes = k が max_depth = k-1 に匹敵する結果を与えるが、訓練するのがはるかに速いことを発見したが、わずかに高いトレーニング誤差を犠牲にしている。 max_leaf_nodes パラメータは[F2001]の勾配ブーストに関する章の変数 J に対応し、 max_leaf_nodes == interaction.depth + 1 の R's gbm パッケージの interaction.depth パラメータに関連しています。
1.11.4.5. 数学的処方
GBRTは、以下の形式の加法モデルを考慮する:
F(x) = \sum_{m=1}^{M} \gamma_m h_m(x)
ここで、 $h_m(x)$ は、通常、ブースティングのコンテキストで弱学習器と呼ばれる基底関数です。 Gradient Tree Boostingは、固定サイズの 決定木 を弱学習器として使用します。ディシジョンツリーには、混合型のデータを扱う能力と複雑な特徴量をモデル化する能力を高めるために、ブースティングに役立ついくつかの能力があります。
他のブースティングアルゴリズムと同様に、GBRTは加算器モデルを順方向の段階で構築します。
F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)
各段階において、決定木 $h_m(x)$ は、現在のモデル $F_{m-1}$ 及びその適合 $F_{m-1}(x_i)$ が与えられたときの損失関数 $L$ を最小にするように選択される。
F_m(x) = F_{m-1}(x) + \arg\min_{h} \sum_{i=1}^{n} L(y_i,
F_{m-1}(x_i) - h(x))
初期モデル $F_{0}$ は問題に固有であり、最小2乗回帰のために通常は目標値の平均を選択する。
注意: 初期モデルは、init引数で指定することもできます。渡されたオブジェクトはフィット感と予測を実装する必要があります。
勾配ブーストは、最急降下を介してこの最小化問題を数値的に解くことを試みます。最も急峻な降下方向は、微分可能な任意の損失関数について計算できる現行モデル $F_{m-1}$ で評価される損失関数の負の勾配です。
F_m(x) = F_{m-1}(x) + \gamma_m \sum_{i=1}^{n} \nabla_F L(y_i,
F_{m-1}(x_i))
行の長さを指定してステップ長 $\gamma_m$ を選択すると、
\gamma_m = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, F_{m-1}(x_i)
- \gamma \frac{\partial L(y_i, F_{m-1}(x_i))}{\partial F_{m-1}(x_i)})
回帰と分類のためのアルゴリズムは、使用される具体的な損失関数でのみ異なります。
1.11.4.5.1. 損失関数
以下の損失関数がサポートされており、パラメータ loss を使用して指定することができます。
- 回帰
- 最小二乗(
'ls'):優れた計算特性に起因する回帰の自然選択。初期モデルは、目標値の平均によって与えられる。 - 最小絶対偏差(
'lad'):回帰のロバストロス関数。初期モデルは、目標値の中央値によって与えられる。 - Huber(
'huber'):最小自乗と最小絶対偏差を組み合わせたもう1つのロバストロス関数。アウトライアに関して感度を制御するためにalphaを使用する(詳細は [F2001] を参照)。 - Quantile(
'quantile'):分位回帰の損失関数。分位数を指定するには、0 < alpha < 1を使用します。この損失関数を使用して予測間隔を作成することができます(勾配ブースト回帰の予測間隔を参照)。
- 最小二乗(
- 分類
- 二項分類(
'deviance'):二項分類のための負の二項対数尤度損失関数(確率推定を提供する)。初期モデルは対数オッズ比によって与えられる。 - 多項式偏差(
'deviance'):相互排他的なクラスn_classesを持つ多クラス分類のための負の多項対数 - 尤度損失関数。それは確率推定を提供する。初期モデルは、各クラスの事前確率によって与えられる。繰り返しのたびに、多数のクラスを持つデータセットではGBRTをむしろ非効率にする回帰ツリーを構築する必要があります。 - 指数関数的な損失(
'exponential'): AdaBoostClassifier と同じ損失関数。'deviance'よりも誤ったラベルを付けられた例はあまり強くありません。バイナリ分類にのみ使用できます。
- 二項分類(
1.11.4.6. 正規化
1.11.4.6.1. 収縮
[F2001]は、各弱学習器の寄与を因子でスケーリングする簡単な正則化戦略を提案しました。 $\nu$ :
F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)
パラメータ $\nu$ は勾配降下手順のステップ長さをスケーリングするので 学習率 とも呼ばれます。 learning_rate パラメータを使用して設定できます。
パラメータ learning_rate は、弱学習器の数に合致するパラメータ n_estimators と強く対話します。 learning_rate の値が小さいほど、一定のトレーニングエラーを維持するために、より多くの弱学習器が必要になります。経験的な証拠によると、 learning_rate の値が小さいほどテストエラーが改善されることを示しています。 [HTF2009]は、学習率を小さな定数(例えば、 learning_rate <= 0.1 )に設定し、早期停止によって n_estimators を選択することを推奨しています。 learning_rate と n_estimators の相互作用の詳細については、[R2007]を参照してください。
1.11.4.6.2. サブサンプリング
[F1999]は、勾配ブーストとブートストラップ平均(バギング)を組み合わせた確率的勾配ブーストを提案しました。各反復において、基本分類器は、利用可能な訓練データの小数 subsample について訓練される。サブサンプルは置換せずに描画されます。 subsample の典型的な値は0.5です。
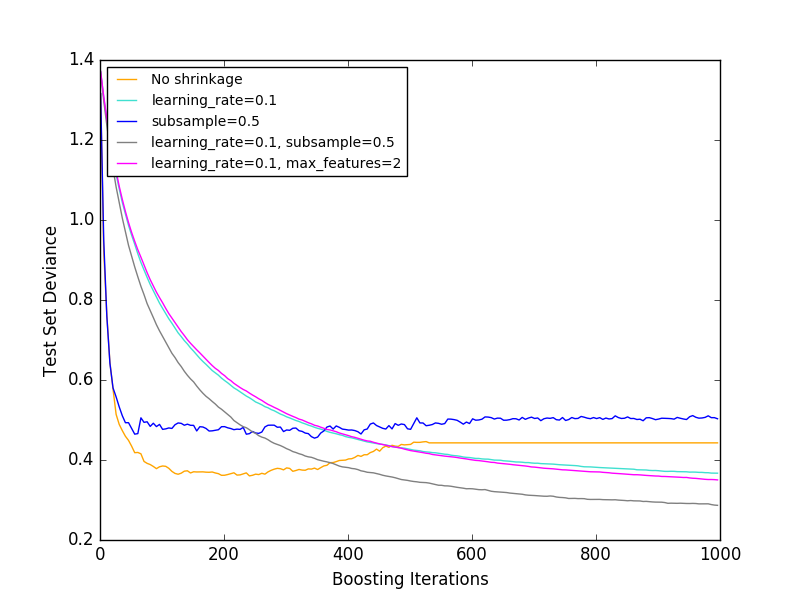
下の図は、収縮とサブサンプリングがモデルの適合度に及ぼす影響を示しています。収縮が収縮しないことが明らかに分かります。収縮を伴うサブサンプリングは、モデルの精度をさらに高めることができる。一方、収縮のないサブサンプリングは、あまりうまくいかない。
分散を減らすもう1つの戦略は、 RandomForestClassifier でランダムな分割に類似する特徴量をサブサンプリングすることです。サブサンプリングされた特徴量の数は、 max_features パラメータによって制御できます。
注意: max_featuresの値を小さくすると、ランタイムが大幅に減少する可能性があります。
確率的勾配ブースティングは、ブートストラップサンプルに含まれない例(すなわち、バッグ外れの例)に対する逸脱の改善を計算することによって、テスト逸脱の袋外推定を計算することを可能にする。改善は属性 oob_improvement_ に格納されます。 oob_improvement_[i] は、現在の予測にi番目のステージを追加すると、OOBサンプルの損失に関する改善を保持します。最適な反復回数の決定など、モデル選択にアウトオブバッグの推定を使用できます。 OOBの推定器は通常非常に悲観的であるため、代わりに相互検証を使用し、相互検証が時間がかかり過ぎる場合にのみOOBを使用することをお勧めします。
1.11.4.7. 解釈
個々の決定木は、単に木構造を視覚化するだけで簡単に解釈できます。しかし、勾配ブースティングモデルは何百もの回帰木を含んでいるため、個々の樹木の目視検査によって容易に解釈することはできません。幸いにも、勾配ブースティングモデルを要約し、解釈するための多くの技術が提案されている。
1.11.4.7.1. 特徴量の重要性
多くの場合、特徴量は目標応答を予測するために均等に貢献しません。多くの場合、特徴量の大半は実際には無関係です。モデルを解釈するとき、最初の質問は通常、それらの重要な特徴量は何か、そしてそれらが目標応答の予測にどのように貢献しているかということです。
個々の決定木は、本質的に、適切な分割点を選択することによって特徴量選択を実行する。この情報は、各特徴量の重要度を測定するために使用できます。基本的な考え方は、ツリーの分割ポイントで特徴量が使用される頻度が高いほど特徴量が重要になることです。この重要な概念は、各ツリーの特徴量重要度を単純に平均化することによって、意思決定ツリーアンサンブルに拡張することができます(詳細については、 重要度評価 を参照してください)。
フィット勾配ブースティングモデルの特徴量重要度スコアは、feature_importances_ プロパティからアクセスできます。
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([ 0.11, 0.1 , 0.11, ...
- 例:
1.11.4.7.2. 部分依存
部分依存性プロット(PDP)は、ターゲット応答と他のすべての特徴量(「補完」特徴量)の値を周縁化する「ターゲット」特徴量のセットとの間の依存性を示す。 直観的に、我々は、部分的依存を、「目標」特徴量[2]の関数として、期待される目標応答[1]として解釈することができる。
人間の知覚の限界のため、ターゲット特徴量セットのサイズは小さくなければならず(通常は1つまたは2つ)、したがって、ターゲット特徴量は通常最も重要な特徴量の中から選択される。
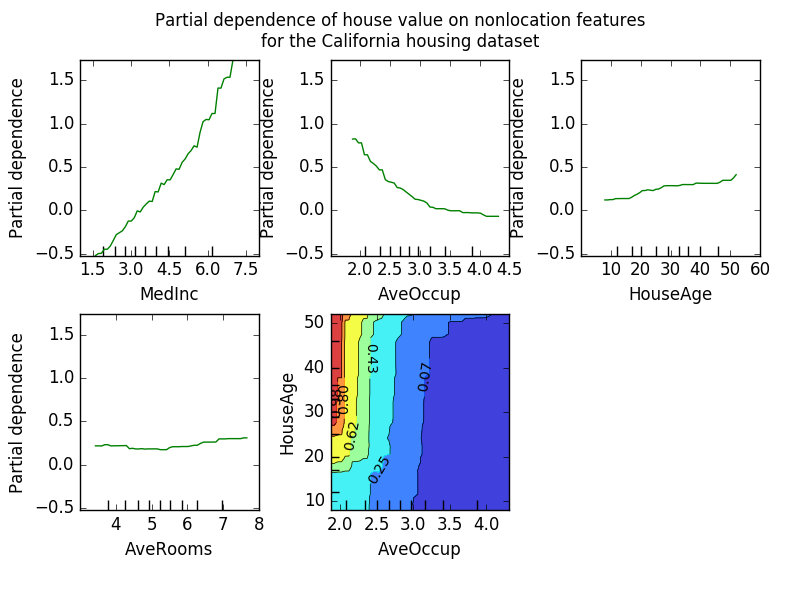
下の図は、カリフォルニア州の住宅データセットの4つの一方向および一方向の部分依存プロットを示しています。
一方向PDPは、ターゲット応答とターゲット特徴量(例えば、線形、非線形)との間の相互作用について教えている。上記の図の左上のプロットは、地区内の平均収入が住宅価格の中央値に与える影響を示しています。我々はそれらの間に線形関係がはっきりと見える。
2つのターゲット特徴量ーを有するPDPは、2つの特徴量ー間の相互作用を示す。例えば、上の図の2変数PDPは、住宅価格の中央値が家計年齢と平均のジョイント値にどのように依存するかを示しています。世帯あたりの占有者数。 2つの特徴量の間の相互作用を明確に見ることができます。 2人以上の場合、家の価格は家の年齢にほとんど依存しないのに対し、2人未満の場合は年齢に強く依存する。
モジュール partial_dependence は、片方向と双方向の部分依存関係プロットを作成する便利な関数 plot_partial_dependence を提供します。以下の例では、部分依存グラフのグリッドを作成する方法を示します。特徴量 0 と 1 の2つの一方向PDPと、2つの特徴量間の双方向PDPです。
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.ensemble.partial_dependence import plot_partial_dependence
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> fig, axs = plot_partial_dependence(clf, X, features)
マルチクラスモデルの場合、 label 引数を使用してPDPを作成するクラスラベルを設定する必要があります。
>>>
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
... max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> fig, axs = plot_partial_dependence(mc_clf, X, features, label=0)
プロットではなく部分依存関数の生の値が必要な場合は、 partial_dependence 関数を使うことができます:
>>>
>>> from sklearn.ensemble.partial_dependence import partial_dependence
>>> pdp, axes = partial_dependence(clf, [0], X=X)
>>> pdp
array([[ 2.46643157, 2.46643157, ...
>>> axes
[array([-1.62497054, -1.59201391, ...
関数は、部分依存関数を評価すべき対象特徴量の値を指定する引数 grid 、またはトレーニングデータからグリッドを自動的に作成するための簡易モードである引数 X のいずれかを必要とする。 X が指定されている場合、関数によって返された軸の値は各ターゲット特徴量の軸になります。
grid 内の「ターゲット」特徴量の各値について、部分依存関数は、「補完」特徴量のすべての可能な値にわたるツリーの予測を疎遠にする必要がある。決定木では、この機能は、トレーニングデータを参照することなく効率的に評価することができます。各グリッドポイントについて、重み付けされたツリートラバーサルが実行される:分割されたノードに「ターゲット」特徴量が含まれている場合、対応する左または右に分岐します。それ以外の場合は両方の分岐を追います。各枝には、その枝に入ったトレーニングサンプルの割合が加重されます。最後に、部分依存性は、訪問されたすべてのリーフの加重平均によって与えられます。ツリーアンサンブルの場合、個々のツリーの結果は再び平均化されます。
-
脚注
- [1]損失= '逸脱'の分類では、目標応答はlogit(p)です。
- [2]より正確には、初期モデルを考慮した後の目標応答の期待。部分依存グラフにはinitモデルは含まれていません。
-
例:
-
参考文献
- [F2001](1、2、3)J.フリードマン、 "貪欲関数近似:勾配ブーストマシン"、統計年報、Vol。 29巻、5号、2001年。
- [F1999] フリードマン、「確率的勾配ブースト」、1999
- [HTF2009] Hastie、R. TibshiraniおよびJ.Friedman、 "Elements of Statistical Learning Ed。 2 "、Springer、2009。
- [R2007] Ridgeway、 "Generalized Boosted Models:gbmパッケージのガイド"、2007
1.11.5. VotingClassifier
投票分類器実装の背後にあるアイデアは、概念的に異なる機械学習分類器を組み合わせ、多数決または平均予測確率(ソフト投票)を使用してクラスラベルを予測することである。そのような分類器は、個々の弱点を釣り合わせるために、同様に良好に機能するモデルのセットに有用であり得る。
1.11.5.1. 大多数のクラスのラベル(多数決/厳選)
過半数投票では、特定のサンプルの予測クラスラベルは、個々の分類子によって予測されるクラスラベルの大部分(モード)を表すクラスラベルです。
たとえば、与えられたサンプルの予測が
- 分類器1 → クラス1
- 分類器2 → クラス1
- 分類器3 → クラス2
VotingClassifier( voting = 'hard' )は、多数クラスラベルに基づいてサンプルを「クラス1」として分類します。
同値の場合、VotingClassifierは昇順のソート順に基づいてクラスを選択します。たとえば、次のシナリオでは
- 分類器1 → クラス2
- 分類器2 → クラス1
クラスラベル1がサンプルに割り当てられます。
1.11.5.1.1. 使用法
次の例は、多数決ルール分類器を適合させる方法を示しています。
>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier
>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')
>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
... scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
... print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.90 (+/- 0.05) [Logistic Regression]
Accuracy: 0.93 (+/- 0.05) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.05) [Ensemble]
1.11.5.2. 加重平均確率(ソフト投票)
大多数の投票(ハード投票)とは対照的に、ソフト投票はクラスラベルを予測確率の合計のargmaxとして返します。
特定の重みは、 weights パラメータを介して各分類器に割り当てることができる。重みが与えられると、各分類器について予測されたクラス確率が収集され、分類器重みが乗算され、平均化される。最後のクラスラベルは、最も高い平均確率を有するクラスラベルから導出される。
これを簡単な例で説明すると、 w1=1 、 w2=1 、 w3=1 の3つの分類子と、すべての分類子に等しい重みを割り当てる3クラスの分類問題があるとします。
サンプルの加重平均確率は、次のように計算されます。
| 分類器 | クラス1 | クラス2 | クラス3 |
|---|---|---|---|
| 分類器1 | w1 * 0.2 | w1 * 0.5 | w1 * 0.3 |
| 分級機2 | w2 * 0.6 | w2 * 0.3 | w2 * 0.1 |
| 分類器3 | w3 * 0.3 | w3 * 0.4 | w3 * 0.3 |
| 加重平均 | 0.37 | 0.4 | 0.23 |
ここで、予測クラスラベルは、平均確率が最も高いので、2である。
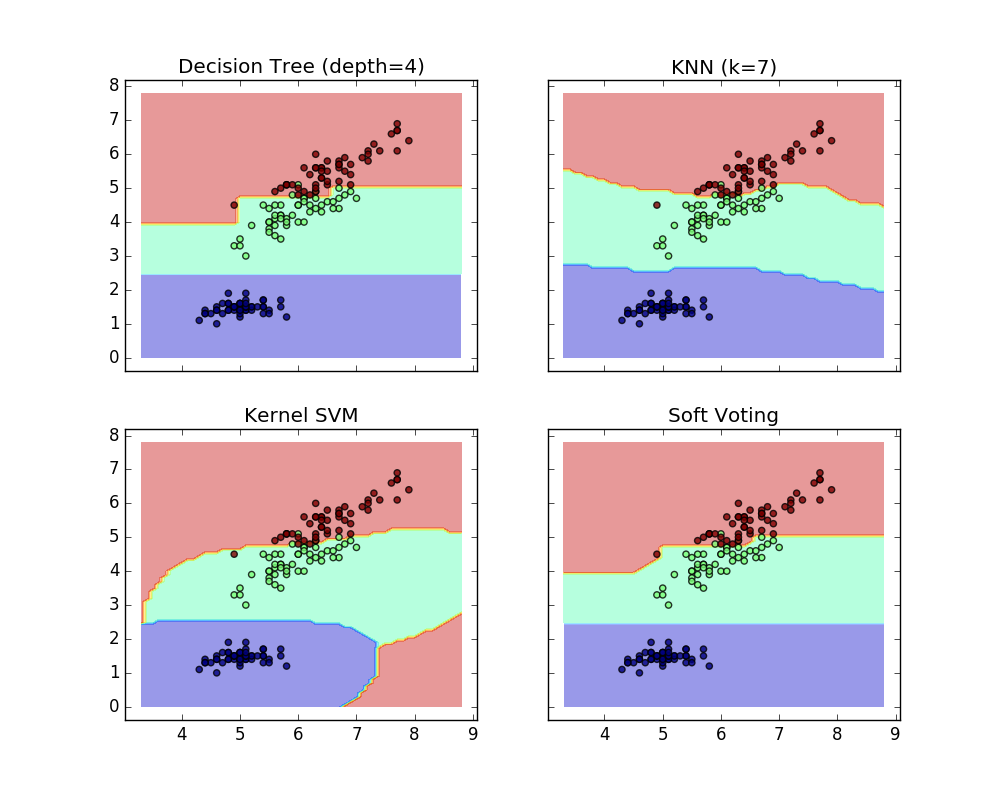
次の例は、線形サポートベクトルマシン、決定木、およびK最近傍の分類子に基づいてソフトVotingClassifierが使用されたときに、決定領域がどのように変化するかを示しています。
>>> from sklearn import datasets
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.svm import SVC
>>> from itertools import product
>>> from sklearn.ensemble import VotingClassifier
>>> # Loading some example data
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [0,2]]
>>> y = iris.target
>>> # Training classifiers
>>> clf1 = DecisionTreeClassifier(max_depth=4)
>>> clf2 = KNeighborsClassifier(n_neighbors=7)
>>> clf3 = SVC(kernel='rbf', probability=True)
>>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)], voting='soft', weights=[2,1,2])
>>> clf1 = clf1.fit(X,y)
>>> clf2 = clf2.fit(X,y)
>>> clf3 = clf3.fit(X,y)
>>> eclf = eclf.fit(X,y)
1.11.5.3. GridSearchでVotingClassifierを使用する
VotingClassifierは、個々の推定器のハイパーパラメータを調整するために、GridSearchと一緒に使用することもできます。
>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200],}
>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)
1.11.5.3.1 使用法
予測されたクラス確率に基づいてクラスラベルを予測するために(VotingClassifierのscikit-lear estimatorsはpredict_probaメソッドをサポートしなければならない)
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
オプションで、個々の分類子に重み付けを行うことができます。
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft', weights=[2,5,1])
scikit-learn 0.18 ユーザーガイド 1. 教師付き学習 より
©2010 - 2016、scikit-learn developers(BSDライセンス)。