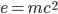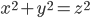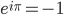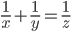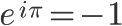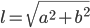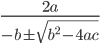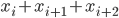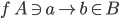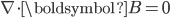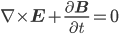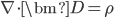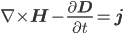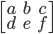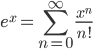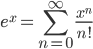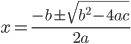動機
Qiitaに数式を楽に書ける記法があると嬉しいよね…
というか今どき数式が書けないとかないわー…
Qiita に数式を貼ろう
これはGoogle Chart APIを使って、

のように画像として貼り込んでいます。
でもこんなエンコードされたURLを記述するの面倒ですよね!
はてな風の
先ほどの数式なら、例えばこんな風に書けると捗ります。
[tex:f^\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}]
でもQiita独自のmarkdown仕様拡張とか出来ればしてほしくないし。
そこで
…と思ってブラウザ拡張を作ってみました。
とりあえず Chrome Extension と greasemonkey を用意してあります。
昨日作ったKobito-Evernote同期スクリプト (kobitonote)と合わせてqiita-toolkitというプロジェクトに収録しています。
git clone git://github.com/naoyat/qiita-toolkit.git
Qiitaで編集画面を開くと、「編集」「プレビュー」の右に「»md」「»tex」というリンクが追加されます。
はてな風 記法 → markdown
記法 → markdown
ほにゃらら [tex:e=mc^2] ほにゃららん
»md をクリック
ほにゃらら  ほにゃららん
これで保存すると、無事
のように表示されます。
markdown →はてな風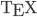 記法
記法
前に書いた数式を修正したい時など、元の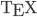
ほにゃらら  ほにゃららん
»tex をクリック
ほにゃらら [tex:e=mc^2] ほにゃららん
どうでしょう?
使用例
各所から集めてきたはてなの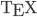
画像が壊れているのは、mimetexでは使えるけれどGoogle Chart APIでは使えない命令が使われている物と思われます。
http://d.hatena.ne.jp/tt_clown/20100205/1265350752
[tex:x^2 + y^2 = z^2]
[tex:e^{i\pi} = -1]
[tex:\frac{1}{x} + \frac{1}{y} = \frac{1}{z}]
http://d.hatena.ne.jp/edvakf/20090530/1243672072
[tex:{\Huge e^{i\pi}=-1}]
http://adiary.blog.abk.nu/063
[tex:l=\sqrt{a^2+b^2}]
[tex:\frac{2a}{-b\pm\sqrt{b^2-4ac}]
[tex:x_{i}+x_{i+1}+x_{i+2}]
[tex:f\:A \ni a \rightarrow b \in B]
http://d.hatena.ne.jp/tequilasunset/20101117/p1
[tex:f^\prime(x)=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}]
[tex:f(x)=\int_{-\infty}^x e^{-t^2}dt]

[tex:\nabla\cdot\boldsymbol{B} = 0]
[tex:\nabla\times\mathbf{E}+\frac{\partial\mathbf{B}}{\partial t}=\mathbf{0}]
[tex:\nabla\cdot\bm{D}={\rho}]
[tex:\nabla\times\mathbf{H}-\frac{\partial\mathbf{D}}{\partial t}=\mathbf{j}]
[tex:i\hbar\frac{\partial{}}{\partial{}t}|\psi(t)\rangle=\hat{H}|\psi(t)\rangle]
[tex:\delta S=\sum_{i=1}^N\left\[\frac{\partial L}{\partial\dot{q}_{k}}\delta q_k\right\]_{t_1}^{t_2}+\sum_{i=1}^N\int_{t_1}^{t_2}\left(\frac{\partial L}{\partial q_k}-\frac{d}{d t}\frac{\partial L}{\partial \dot{q}_k}\right)\delta q_k dt]
[tex:D={f\in L^2(\R, dx) : \frac{df}{dx} \in L^2(\R, dx)}]
[tex:\begin{bmatrix} a&b&c \\ d&e&f \end{bmatrix}]
[tex:A = \large\left(\begin{array}{c.cccc} &1&2&\cdots&n\\ \hdash 1&a_{11}&a_{12}&\cdots&a_{1n}\\ 2&a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ n&a_{n1}&a_{n2}&\cdots&a_{nn} \end{array}\right)]
[tex:\normalsize\left(\large\begin{array}{GC+23} \varepsilon_x\\ \varepsilon_y\\ \varepsilon_z\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}\right) {\Large=} \left\[\begin{array}{CC} \begin{array}\frac{1}{E_{\fs{+1}x}}&-\frac{\nu_{xy}}{E_{\fs{+1}x}}&-\frac{\nu_{\fs{+1}xz}}{E_{\fs{+1}x}}\\ -\frac{\nu_{yx}}{E_y}&\frac{1}{E_{y}}&-\frac{\nu_{yz}}{E_y}\\ -\frac{\nu_{\fs{+1}zx}}{E_{\fs{+1}z}}&-\frac{\nu_{zy}}{E_{\fs{+1}z}}&\frac{1}{E_{\fs{+1}z}}\end{array}&{\LARGE 0}\\ {\LARGE 0}&\begin{array}\frac{1}{G_{xy}}&&\\ &\frac{1}{G_{\fs{+1}xz}}&\\&&\frac{1}{G_{yz}} \end{array} \end{array}\right\] \left(\large\begin{array} \sigma_x\\ \sigma_y\\ \sigma_z\\ \tau_{xy}\\ \tau_{xz}\\ \tau_{yz} \end{array}\right)]
mimetexのサンプルから
mimetexでは\large以上で\displaystyle扱いにしてくれますが、Google Chart APIでは\displaystyleと明記する必要があります
[tex:f(x)=\int_{-\infty}^x e^{-t^2}dt]

[tex:e^x=\sum_{n=0}^\infty\frac{x^n}{n!}]
[tex:\displaystyle e^x=\sum_{n=0}^\infty\frac{x^n}{n!}]
[tex:e^x=\lim_{n\to\infty} \left(1+\frac~xn\right)^n]
[tex:f^\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}]
[tex:x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}]
[tex:f(x) = \frac1{\sigma\sqrt{2\pi}} \int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt]
[tex:\displaystyle f(x) = \frac1{\sigma\sqrt{2\pi}} \int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt]


余談
Google Chart API は(当然のことながら)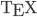
// from Google Chart API入門