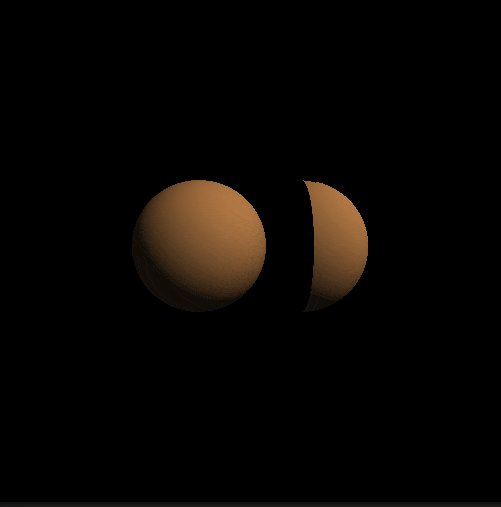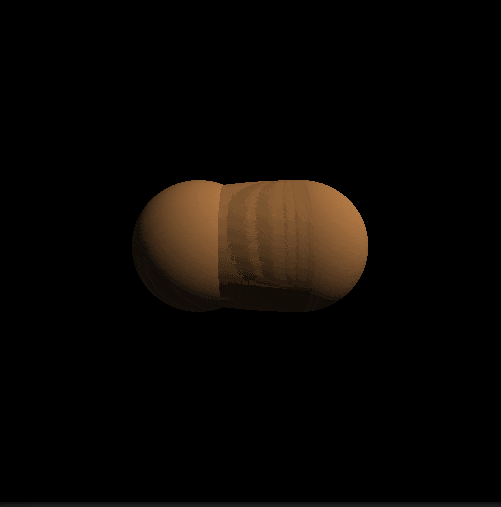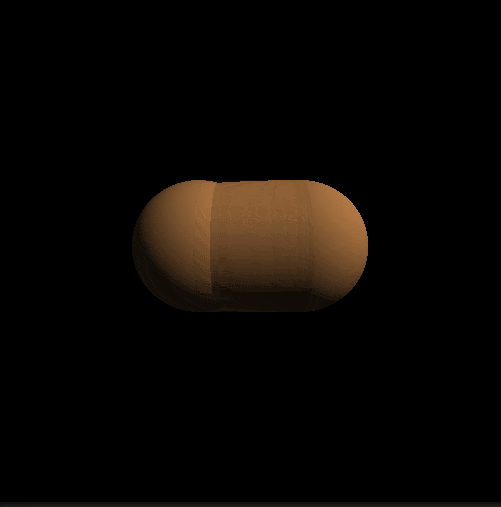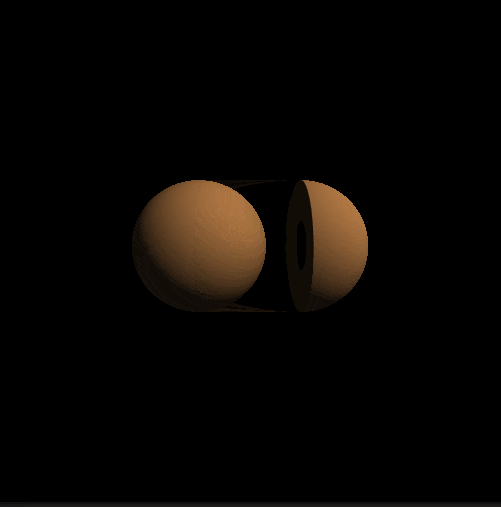modeling with distance functionsの距離関数の一覧に沿って記事を書いています.
cupsuleの距離関数は,
vec3 pa = p - a, ba = b - a;
float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0);
return length( pa - ba*h ) - r;
数式に直すと
\left\{
\begin{array}{ll}
\vec{p}=(p_x, p_y, p_z), \vec{a}=(a_x, a_y, a_z), \vec{b}=(b_x, b_y, b_z) \\
h = min(max(\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}}, 0.0), 1.0) \\
\| (\vec{p} - \vec{a}) - h(\vec{b} - \vec{a}) \| - r = 0
\end{array}
\right.
記号の説明
\| \alpha \|:距離のこと \\
\vec{p}:ベクトル
とりあえず、なんでこれで、cupsuleになるのや?
と思いの方!
とりあえず、
\| (\vec{p} - \vec{a}) - h(\vec{b} - \vec{a}) \| - r
を考えます.
一旦, h は、面倒なので 1.0 とか 2.0 とかの定数として考えます..
すると
\| \vec{p} + (h-1)\vec{a} - h\vec{b} \| - r
で、また面倒なので、
\vec{p} + (h-1)\vec{a} - h\vec{b} を \vec{v}=(v_x, v_y, v_z) とか適当に置きます.
で, 書き直すと
\sqrt{(p_x-v_x)^2 + (p_y-v_y)^2 + (p_z-v_z)^2} - r
となります.
なんとこれ h を x,y,z に依存しない定数とみなすと球になるんですね.
ということは、予測ですが、cupsuleの両端の丸みは、球で描かれているのではないか?
と予測できます!
で、本題
cupsuleのあの胴長の円柱の鍵は、h にありです.
h = \min(\max(\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}}, 0.0), 1.0)
をmin と max を使わずきっちり書いてみましょう.
h = \left\{
\begin{array}{ll}
0.0 & (\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}} < 0) \\
\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}} & (0 < \frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}} < 1) \\
1.0 & (\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}} > 1)
\end{array}
\right.
となります.
ということは、ここでglslの距離関数に立ち返ると,
vec3 pa = p - a, ba = b - a;
float d = dot(pa,ba)/dot(ba,ba);
if(d < 0.0){
return length(pa) - r;
} else if(d > 1.0){
return length( pa - ba ) - r;
}
return length( pa - ba * d ) - r;
ということは,
それぞれ
return length(pa) - r;
return length( pa - ba ) - r;
return length( pa - ba * d ) - r;
を描画すると
return length(pa) - r;
return length( pa - ba ) - r;
return length( pa - ba * d ) - r;
とま~、三つが組み合わさっているのがわかります.
で、最後に、
return length( pa - ba * d ) - r;
の形は、なんで円柱型になるの?を説明にして終わります.
length( pa - ba * d ) - r
数式で書くと
\| (\vec{p} - \vec{a}) - d(\vec{b} - \vec{a}) \| - r
ここで、
\| (\vec{p} - \vec{a}) - (\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}})(\vec{b} - \vec{a}) \| - r
ここからの計算は、頭が痛くなるので,(だいぶ緩い計算をします.)
\begin{align}
&\| (\vec{p} - \vec{a}) - (\frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}})(\vec{b} - \vec{a}) \| \\
&= \sqrt{\alpha_1 x^2 + \alpha_2 y^2 + \alpha_3 z^2 + \alpha_4 xy + \alpha_5 yz + \alpha_6 zx} \; (\alpha_n (n=1,2,3,4,5,6) は、適当にまとめた定数)
\end{align}
の形になり描画するのと円柱になります(ここら辺の計算書きたくないので、省略します…)
d の導出方法
(\vec{p} - \vec{a}) - d(\vec{b} - \vec{a}) と (\vec{b} - \vec{a}) が直行したと考えると \\
((\vec{p} - \vec{a}) - d(\vec{b} - \vec{a})) \cdot (\vec{b} - \vec{a}) = 0 なので、\\
hについてまとめると \\
d = \frac{(\vec{p} - \vec{a}) \cdot (\vec{b} - \vec{a})}{ \| \vec{b} - \vec{a} \|^{2}}
ちなみに d についての補足
d は書き方を変えると
\begin{align}
d &= \frac{|\vec{p} - \vec{a}||\vec{b} - \vec{a}| \cos \theta}{|\vec{b} - \vec{a}|^2} \\
&= \frac{|\vec{p} - \vec{a}| \cos \theta}{|\vec{b} - \vec{a}|} \\
\end{align} \\
と|\vec{p} - \vec{a}|の線分baへの射影と|\vec{b} - \vec{a}|の比とも見れますね.
dの変化を見てみる.
vec3 pa = p - a, ba = b - a;
float ipr = dot(pa,ba)/(dot(ba,ba)*abs(sin(time)));
float h = clamp(ipr, 0.0, 1.0);
return length( pa - ba*h ) - r;
dot(ba,ba)*abs(sin(time)) の変化がいかに、円柱部分を作っていたか分かります.
// ============================================================================
// Capsule / Line function_01
// ============================================================================
precision mediump float;
uniform vec2 resolution; // resolution (512.0, 512.0)
uniform vec2 mouse; // mouse (-1.0 ~ 1.0)
uniform float time; // time (1second == 1.0)
uniform sampler2D prevScene; // previous scene texture
// Capsule / Lineの距離関数
float sdCapsule(vec3 p)
{
// 回転
// mat3 m_x = mat3(1,0,0,0,cos(time),-sin(time),0,sin(time),cos(time));
// p = m_x * p;
// mat3 m_y = mat3(cos(time),0,-sin(time),0,1,0,sin(time),0,cos(time));
// p = m_y * p;
// mat3 m_z = mat3(cos(time),-sin(time),0,sin(time),cos(time),0,0,0,1);
// p = m_z * p;
vec3 a = vec3(0.75, 0.0, 1.0);
vec3 b = vec3(-0.75, 0.0, 1.0);
float r = 1.0;
/* 元の距離関数 */
vec3 pa = p - a, ba = b - a;
float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0);
return length( pa - ba*h ) - r;
/* 距離関数1 */
// vec3 pa = p - a, ba = b - a;
// float h = min(max( dot(pa,ba)/dot(ba,ba), 0.0), 1.0);
// return sqrt((p.x-h*ba.x)*(p.x-h*ba.x)+(p.y-h*ba.y)*(p.y-h*ba.y)+(p.z-h*ba.z)*(p.z-h*ba.z))- r;
/* 距離関数2 */
// vec3 pa = p - a, ba = b - a;
// float d = dot(pa,ba)/dot(ba,ba);
// if(d < 0.0){
// return length(pa) - r;
// } else if(d > 1.0){
// return length( pa - ba ) - r;
// }
// return length( pa - ba * d ) - r;
/* dの変化を見る_1 */
// vec3 pa = p - a, ba = b - a;
// float ipr = dot(pa,ba)/(dot(ba,ba)*abs(sin(time)));
// float h = clamp(ipr, 0.0, 1.0);
// return length( pa - ba*h ) - r;
/* dの変化を見る_2 */
// vec3 pa = p - a, ba = b - a;
// float ipr = (dot(pa,ba)/dot(ba,ba))*abs(sin(time));
// float h = clamp(ipr, 0.0, 1.0);
// return length( pa - ba*h ) - r;
/* dの変化を見る_3 */
// vec3 pa = p - a, ba = b - a;
// float ipr = dot(pa,ba)/dot(ba,ba);
// float h = clamp(abs(sin(ipr+time)), 0.0, 1.0);
// return length( pa - ba*h ) - r;
}
// 距離関数を呼び出すハブ関数
float distanceHub(vec3 p){
return sdCapsule(p);
}
// 法線を生成する
vec3 genNormal(vec3 p){
float d = 0.001;
return normalize(vec3(
distanceHub(p + vec3( d, 0.0, 0.0)) - distanceHub(p + vec3( -d, 0.0, 0.0)),
distanceHub(p + vec3(0.0, d, 0.0)) - distanceHub(p + vec3(0.0, -d, 0.0)),
distanceHub(p + vec3(0.0, 0.0, d)) - distanceHub(p + vec3(0.0, 0.0, -d))
));
}
void main(){
// スクリーンスペースを考慮して座標を正規化する
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// カメラを定義する
vec3 cPos = vec3(0.0, 0.0, 5.0); // カメラの位置
vec3 cDir = vec3(0.0, 0.0, -1.0); // カメラの向き(視線)
vec3 cUp = vec3(0.0, 1.0, 0.0); // カメラの上方向
vec3 cSide = cross(cDir, cUp); // 外積を使って横方向を算出
float targetDepth = 1.0; // フォーカスする深度
// カメラの情報からレイを定義する
vec3 ray = normalize(cSide * p.x + cUp * p.y + cDir * targetDepth);
// マーチングループを組む
float dist = 0.0; // レイとオブジェクト間の最短距離
float rLen = 0.0; // レイに継ぎ足す長さ
vec3 rPos = cPos; // レイの先端位置(初期位置)
for(int i = 0; i < 32; ++i){
dist = distanceHub(rPos);
rLen += dist;
rPos = cPos + ray * rLen;
}
// レイとオブジェクトの距離を確認
if(abs(dist) < 0.001){
// 法線を算出
vec3 normal = genNormal(rPos);
// ライトベクトルの定義
vec3 light = normalize(vec3(1.0, 1.0, 1.0));
// ライトベクトルとの内積を取る
float diff = max(dot(normal, light), 0.1);
// gl_FragColor = vec4(vec3(diff, diff, diff), 1.0);
gl_FragColor = vec4(vec3(diff*177.0/255.0, diff*120.0/255.0, diff*68.0/255.0), 1.0);
}else{
// 衝突しなかった場合はそのまま黒
gl_FragColor = vec4(vec3(0.0, 0.0, 0.0), 1.0);
}
}