Box-Muller法による正規分布列生成

Qiitaにおける数式の表示、画像の表示の練習も兼ねて。

間違っていたら教えて下さい(下記に示すBox-Muller法は乱数を2つ求める方法なのですが、その内の一方しか使っていないので、大丈夫なのか…という…)。

また、下記内容は、私自身のブログに書いた内容のコピーです。http://mude.hateblo.jp/?page=1410412272

一様分布から正規分布へ

大抵のプログラミング言語には、擬似乱数を生成するための関数が用意されています。そして、よくあるパターンとしては、その擬似乱数は0.0以上1.0以下の適当な値を返します。ヒストグラムを描くと分かりますが、大抵の場合はどの区間も同じ程度抽出されます(一様分布)。

さて、世の中には正規分布という分布が有ります。正規分布についての説明は端折りますが、正規分布に従う適当な値を出してくれるような便利な関数が常に用意されているとは限りません。一様分布から標準正規分布に変換する方法として、Box-Muller法というのが知られています。それを実際に実装してみましょう。

Box-Muller法

WikipediaのBox-Muller法を見れば分かりますが、方法としては$(0,1)$の一様分布から2つの確率変数(すなわち、乱数)を用意して、示されている式に従ってZ1もしくはZ2を求めれば良さそうです。

例えばZ1であれば、$Z_1=\sqrt{−2 \log X} \cos 2 \pi Y$と書かれているので、これを素直にJavaのプログラムで表現して、

z1 = Math.sqrt(-2.0 * Math.log(x)) * Math.cos(2.0 * Math.pi * y);

とすれば良いですね。ということで、実際のJavaのコードは次の通りです。

ソースコード

BoxMuller.java

import java.util.Random;

public class BoxMuller {
 private Random random;
 private double mu;
 private double sigma;
 private boolean useCosine;
 
 /**
  * Constructor
  * @param mu
  * @param sigma
  * @param useCosine
  */
 public BoxMuller(double mu, double sigma, boolean useCosine){
  random = new Random(System.currentTimeMillis());
 
  this.mu = mu;
  this.sigma = sigma;
  this.useCosine = useCosine;
 }

 /**
  * get next value
  * @return
  */
 public double next(){
  double x = random.nextDouble();
  double y = random.nextDouble();
  double result = 0.0;
 
  if(useCosine){
   result = Math.sqrt(-2.0 * Math.log(x)) * Math.cos(2.0 * Math.PI * y);
  } else {
   result = Math.sqrt(-2.0 * Math.log(x)) * Math.sin(2.0 * Math.PI * y);
  }
  return result * sigma + mu;
 }
}

呼び出すプログラムもついでに。

BoxMullerTest.java

public class BoxMullerTest {
 public static void main(String[] args) {
  BoxMuller boxMuller = new BoxMuller(0,1,true);
  for(int i=0;i<10000;++i){
   System.out.println(boxMuller.next());
  }
 }
}

実行結果

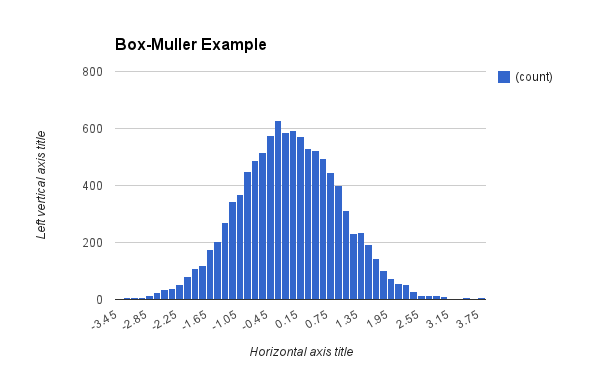
mu=0, sigma=1として、10000回繰り返して値を取り出しました。これは、平均が0、標準偏差が1の正規分布、すなわち標準正規分布を求めることを意味します。

プロットしたグラフが次のとおりです。なんだか良さそうに見えますね。

正規分布は$\pm 1\sigma$の区間に、計算上約68.27%の値が含まれ、$\pm 2\sigma$の区間に、計算上約95.45%の値が$\pm 3\sigma$の区間に、計算上約99.73%の値が含まれます。今回求めた値のうち、その値が$(-1, 1)$に含まれる個数は6678、$(-2, 2)$に含まれる個数は9583、$(-3, 3)$に含まれる個数は9979、それぞれありました。なかなかいい数値のような気がします。

その他

とはいえ、正規分布の乱数列を生成するライブラリを使うのが良いと思います。

数式を書くにも、画像を挿入するのも、とても簡単なことが分かりました。技術的な話については、個人的なブログではなく、Qiitaに貼り付けて行こうと思います。