[WIP] 1-file Chainerを作る

概要

この記事では、Neural NetworkフレームワークであるChainerの最も特徴的なコンセプトである**"Define-by-Run"**を理解するために、手書き数字の分類を行うためのネットワークの記述・学習に必要な最低限の機能だけを持ったライブラリ"1f-chainer"をNumPyのみを使って実装してみます。数式が登場するような説明は全てAppendixに追いやり、本文中ではできるだけコードと文章だけで説明を行うように気をつけて書きました。

本記事で用いた全てのコードは以下に置いてあります：1f-chainer。書き始めると色々なことを追記したくなり間に合わなかったので、今週いっぱいを目処に順次更新していきます。

また、この記事の全ての内容は私個人の見解と理解に基づくものであり、所属する組織とは関係ありません。

想定読者

この記事は、Backpropagationを使ったNeural Networkの訓練について基本的な知識があることと、Python及びNumPyを使用した経験がある方が読むことを想定して書かれています。筆者はあくまでChainerの1ファンなのでChainerに関する所感等は個人の感覚に基づいており、公式見解ではないことにご注意ください。

はじめに

ChainerはNeural Networkを構築し学習するための機能を持つ、Pythonで書かれたフレームワークです。

• 柔軟性が高い（動的なネットワークが書きやすい）
• デバッグが比較的簡単（試行錯誤のサイクルを速くできる）
• 直感的にモデルを記述できる（Pythonでモデルが書ける）

といったことを目指したライブラリだと私は思います。

Neural Networkの構築・学習のためのフレームワーク／ライブラリとして有名なものには、私が知っている限りでも

• TensorFlow
• Torch7
• Caffe (and Caffe2)
• CNTK
• dsstne
• MXNet
• Theano (and Keras, Lasagne, blocks)
• Neon
• DeepLearning4j
• Pylearn2 (開発終了）
• DyNet
• Darknet

などなど、たくさんのものがありますが、バックエンドも含めてPythonのみで書かれたフレームワークは私の知る限り少ない印象です。一方、ChainerはCPU向けのテンソルライブラリとしてNumPyを、GPU向けには独自開発のCuPyを採用していますが、どちらも単体で使える独立したPythonのライブラリであるということがChainerの特徴の一つとなっていると思います。

CuPyは主にCythonを使って書かれており、内部でCUDAカーネルをコンパイル・実行する仕組みを持ちます。またNVIDIAにより開発されているNVIDIA社製GPUの使用を前提としたNeural Networkライブラリ、cuDNNのラッパーも兼ねています。そして、CuPyの大きな特徴は「NumPy互換のAPIを持つ」ということです。これが意味するのは、NumPyを使って書かれたCPU向けのコードを、非常に少ない変更でGPU処理向けに簡単に書き換えることができる（コード中のnumpyという文字列をcupyに置き換えるだけで済む場合もある）ということです。CuPy側がまだサポートしていないNumPyの関数や機能（advanced indexingなど¹）が多くあるため、いろいろな制約や例外はありますが、基本的にCuPyのゴールはCPU用のコードとGPU用のコードを可能な限り近いものにするということにあると思います。

筆者は上に挙げられた主要なフレームワーク／ライブラリの全てを試したわけではないのですが、Chainerが内部で行っているNeural Networkの構築及び学習のための計算手順のデザインには、**"Define-by-Run"**という考え方が用いられており、これが他のフレームワークとChainerを差異化する重要な特徴となっていると思います。"Define by Run"とは、その名のとおりNeural Networkの構造を「実行することによって定義する」という意味です。つまり、実行される前にはまだネットワークがどのような構造になるか決まっておらず、コードが実行されて初めてネットワークの各部分がどのように繋がるのかが決定されるということです。具体的には、ある入力変数が関数の適用を受けたとき、出力が「どのような関数の適用を受けたか」を記憶した新たな変数となっていることで、「実際に行われた計算」ならばあとからいくらでも逆向きに辿っていくことが可能となり、これによって実質的な「計算グラフの実行時構築」を行うというものです。このため、ユーザは「ネットワークの順伝播の計算過程（ルールベースの条件分岐や確率的な条件分岐、または計算過程での新たなレイヤの生成なども含む）」をPythonを用いて記述しておけば、すなわち「フォワード計算を表したコード」を書いておけば、ネットワークの定義を行ったことになるわけです。

こういった特徴を実現するためのいくつかのクラスがChainerの心臓部分となっています。この記事では、Chainerの最も基本的なごく一部分のみを（PythonのWebフレームワーク、Bottleのように）1つのファイルで成り立つライブラリとして自らの手で実装してみることで、その心臓部分を表面的に理解することを目的としています。

ChainerらしくないNeural Networkの実装

まず、もし「Chainerらしい」実装というのを意識せず、できるだけシンプルにNeural Networkの構築と学習を行うコードを書いてみるとどうなるか、を見てみることから始めます。以降本節で現れるコードは、import numpyが冒頭で行われていることを前提とします。また、以降のNeural Networkの学習においては基本的にMini-batched SGDによるパラメータ更新が行われることを想定しています。

LinearレイヤとReLUから成るネットワーク

Linearレイヤと活性化関数ReLUの2種類の層だけからなる三層パーセプトロンは、以下のようにして定義することができます。

class Linear(object):

    def __init__(self, in_sz, out_sz):
        self.W = numpy.random.randn(out_sz, in_sz) * numpy.sqrt(2. / in_sz)
        self.b = numpy.zeros((out_sz,))

    def __call__(self, x):
        self.x = x
        return x.dot(self.W.T) + self.b

    def update(self, gy, lr):
        self.W -= lr * gy.T.dot(self.x)
        self.b -= lr * gy.sum(axis=0)
        return gy.dot(self.W)

class ReLU(object):

    def __call__(self, x):
        self.x = x
        return numpy.maximum(0, x)

    def update(self, gy, lr):
        return gy * (self.x > 0)

model = [
    Linear(784, 100),
    ReLU(),
    Linear(100, 100),
    ReLU(),
    Linear(100, 10)
]

以上です。非常に短く書けることが分かります。上記のLinearレイヤについての詳しい説明は、Appendixとして後述しました：Linearレイヤの基本。また、ReLUレイヤについても簡単に補足説明を書いてあります（ReLUレイヤについて）。

次に、データxと正解tを使ってこの三層パーセプトロンを学習するために必要となる関数forwardとupdateを用意します。

def forward(model, x):
    for layer in model:
        x = layer(x)
    return x

def update(model, gy, lr=0.0001):
    for layer in reversed(model):
        gy = layer.update(gy, lr)

この2つの関数を用いると、上記の三層パーセプトロンの学習を行うことができます。forward関数では、構成レイヤのリストとして与えられるmodelの中身を順に見ていき、データを順伝播させています。update関数では逆に、model内のレイヤを逆順に見ていき、連鎖律で出て来る勾配の掛け算のうち自分より前の部分の総乗であるgyを逆伝播させています。まとめると、学習の手順は

• 推論 : forward関数にデータxを与え、得られた出力をyと置く
• ロス計算 : yと正解tの間の誤差を計算し、yについての勾配を求めgyとおく
• 更新 : backward関数にgyを与え、ネットワーク内の全パラメータを更新

の3ステップとなっています。MNISTデータセットを用いて実際にこれらの処理を繰り返し行い、ネットワークの学習を行うコードは、以下のように書けます。ここでtdは $784$ 次元のベクトルデータが $60000$ 個並んだ(60000, 784)という形のnumpy.ndarrayを表し、tlは $10$ 次元のワンホットベクトル（正解のクラス番号に対応する次元だけが $1$ で、他の次元は全て0となっているベクトル）が $60000$ 個並んだ(60000, 10)という形のnumpy.ndarrayを表すとします。これらの配列を実際に作るコードはAppendixに載せました：データセット読み込み。

def softmax_cross_entropy_gy(y, t):
    return (numpy.exp(y.T) / numpy.exp(y.T).sum(axis=0)).T - t

# 学習
for epoch in range(30):
    for i in range(0, len(td), 128):
        x, t = td[i:i + 128], tl[i:i + 128]
        y = forward(model, x)
        gy = softmax_cross_entropy_gy(y, t)
        update(model, gy)

ミニバッチSGDによる基本的な学習の流れも非常にシンプルであることが分かります。ネットワークはPythonのリストとして定義されているので、forward計算はそのリストの先頭要素に入力変数を与え、得られた出力をそのリストの次の要素の入力として与える、という操作を繰り返すだけで実行できます。パラメータの更新を行うupdate関数では、このリストを「逆順に見て」、後ろから順番にgyを計算し各レイヤのupdateメソッドに渡していけばよいということになります。

ここで、softmax_cross_entropy_gy関数はロス値そのものではなく、ロスの値に対する入力についての勾配を求めて返していることに注意してください。Softmax Cross Entropyロス関数の値とその勾配については、Appendixに書きました：Softmax Cross Entropyの計算と微分。

上記の学習ループを実行したあと、MNISTのValidationデータセットに対する分類精度を調べてみます。

y = forward(model, vd)
n_correct = numpy.sum(vl[numpy.arange(len(vl)), y.argmax(axis=1)])
acc = n_correct / float(len(vl))

print(acc)

ここでvdはValidationデータ、vlはValidationデータに対応したラベルを表し、これらの作り方はTrainingデータと同様にAppendixに書いてあります：データセット読み込み。$30$ エポック学習を行ったのち上記コードでValidationデータでの精度を検証した結果、$0.9674$、つまり $96.74%$ の精度が達成できていることが分かりました。

全体をまとめたコードは右に置いてあります：minimum.py。python minimum.pyで実行すると、学習を行ってValidationデータセットでの精度を表示して終了します。

ChainerらしいNeural Networkの実装

それでは本題です。Neural Networkを構成する基本的なレイヤの実装は、非常に簡単に行えることが分かりました。では、同様のネットワークを定義・訓練するために、Chainerではどのような実装が行われているのでしょうか。

Chainerにおけるforward計算の意味

Chainerでは、冒頭で述べたように**"Define-by-Run"という考え方に基づいてネットワーク構造を定義します。これに対し、上でこれまで説明してきたような実装の方法は"Define-and-Run"と呼ばれ、ネットワークの構造をあらかじめ固定し**、そのあと学習プロセス（forward計算や、backward計算、パラメータの更新など）を実行する、という仕組みでした。そのため、データ如何によってネットワークの構造を変化させる（途中に分岐点がありデータの内容によってどちらの分岐にforwardが進んで行くかが切り替わる、など）ようなことをしようとすると、非常に面倒もしくは不可能なことがあります²。しかし"Define-by-Run"では、forward計算を記述することとネットワーク構造を定義することは同義となり、またforward計算はPythonで記述できるため、分岐や確率的な要素などを含むネットワークでも非常に記述しやすくなります。

それでは、このような柔軟性がどのようにして実現されているのか、順を追って見ていきます。

Chainerを構成している主要なクラスの一部

まず、Chainerには最も根本的な機能を実現するためのいくつかの主要なクラスがあります。

クラス名	機能の概要
Variable	自身に適用された変換を記録しておくことができる変数 ネットワークへの入力変数だけでなく、中間レイヤの入出力、各レイヤのパラメータそのものなども、全てこのクラスのオブジェクトになっている パラメータを表すVariableは、gradメンバ変数に勾配を保持している
Function	パラメータを持たない、もしくは入力変数と一緒に渡されたパラメータを用いて行う変換を表す 入力されたものをinputsメンバ変数に、自身が出力したものをoutputsメンバ変数に保持している
Link	パラメータを持つレイヤ
Chain	複数のLinkをまとめて扱うためのクラス
Optimizer	ChainまたはLinkを受け取り、それらが保持しているパラメータを巡回して更新を行う

VariableとFunction

個人的にChainerのユニークな実装の中心にあるのがこのVariableというクラス（とFunctionクラス）だと思います。"Define-by-Run"を実現するためには、どんなforward計算が実際に行われたかを、計算を実行したあとから辿れるようになっている必要があります。それ自体がネットワークの定義になるからです。その根幹を担うのがこのVariableクラスです。このクラスは、非常にざっくりとした言葉で言うと、どのように自らが生成されたかを覚えている変数です。

Variableは、それがネットワークの根元、つまり入力データを表すVariableでない限り、必ず何らかの関数から出力されたものであるはずです。そこで、どのような関数から出力されたかをcreatorというメンバ変数に保持しておく機能を持たせてやります。

しかしこれだけでは、creatorを見ても自分を出力した関数しか分からず、さらにその前、その関数に入力された変数を生成した関数や、その関数のさらに前の入力を生成した関数・・・といった履歴を辿っていくことができません。そこで、これを可能にするために実際にVariableに対して計算を行うFunctionクラスに、入力されたVariableと出力したVariableの両方を保持させておくようにします。こうすることで、Variableを生成した関数が持つinputから、さらにそれを生成したcreatorを辿っていくことができ、これによってあらゆるVariableからそこに繋がる何らかのリーフノードまでを辿り返すことが可能になります。

また、Variableは当然、値を持つことができる必要があります。そのためdataメンバ変数に配列を保持させることにします。一番根元のルートVariableはデータを表すので、creatorメンバにはNoneを入れることにします。ここまでをまとめると、

• Variable
  • creator: 自身を出力した関数
  • data: 値そのもの
• Function
  • input: 自身に入力されたVariable
  • forward (): inputsを受け取り何らかの計算を行うメソッド
  • output: forward ()で計算された結果

という機能が少なくとも必要そうであることが分かります。VariableとFunctionにこれらの機能をもたせておけば、以下のようにして出力Variableからこれまで行われた計算の履歴を取得することが可能になります。

x = Variable(data)

f_1 = Function()  # Functionオブジェクトの作成
y_1 = f_1(x)      # 内部でVariableのset_creatorが呼ばれ
                  # selfが渡されることで出力 y_1 は f_1
                  # を creator メンバに保持する
f_2 = Function()
y_2 = f_2(y_1)

y_2.creator                      # => f_2
y_2.creator.input                # => y_1
y_2.creator.input.creator        # => f_1
y_2.creator.input.creator.input  # => x

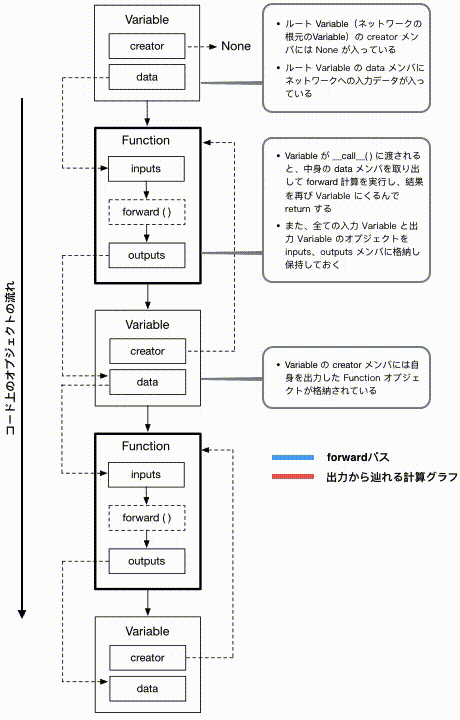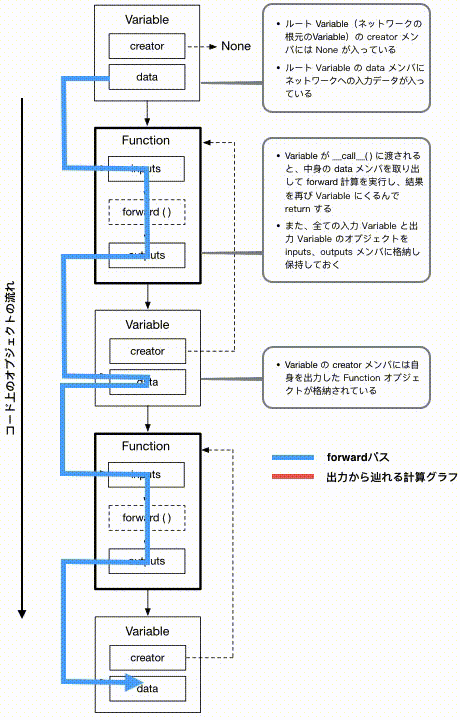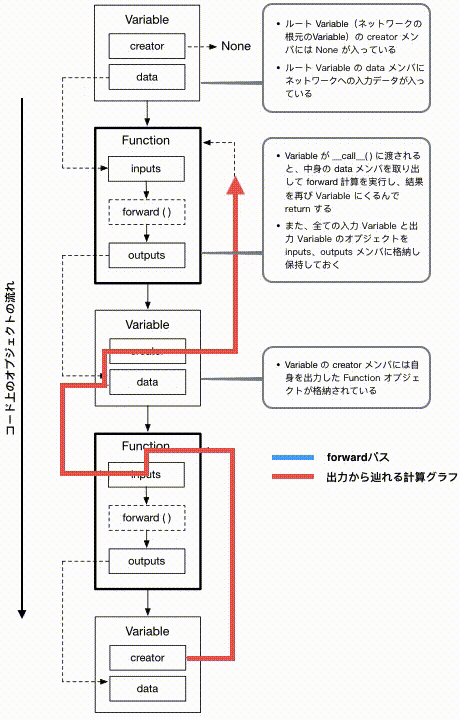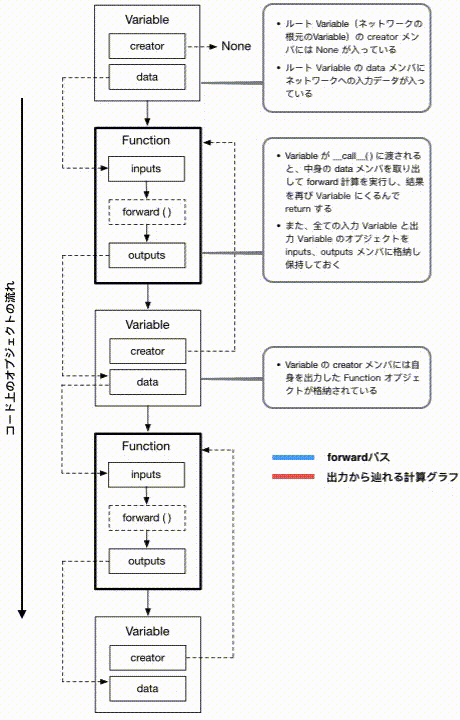
計算の結果得られたy_2から、これを生成したcreatorとそのcreatorが保持しているinputを交互に辿ることで一番根元のVariable、xまでたどり着くことができました。上記の流れを簡単な図で表すと、以下のようになります。

forward計算の流れと逆向き参照による計算グラフ復元

これまでネットワーク上を計算が進んでいった先を「上層」と表現していましたが、この図では便宜上上から下に計算が進む形で書かれています。ご注意ください。

では、この図の上から下に順番にボックスを見ていくと、上記のコードと対応した形で、入力データが順番にFunctionの適用を受け新しいVariableが生成されていく様子が目で追えます。一方、青い矢印は各クラス内での実際のデータの動きを表したもので、赤い矢印はどうやって最終出力Variableからこれまでの計算過程を辿り返すことができるか、を表しています。

Forward計算とネットワークの構築が同時に行えるコード (exp_1.py)

まず、上図の青い矢印に従って実際のforward計算が行えるようにVariableクラスとFunctionクラスのコードを書いてみます。

class Variable(object):

    def __init__(self, data):
        self.data = data
        self.creator = None

    def set_creator(self, gen_func):
        self.creator = gen_func

class Function(object):

    def __call__(self, in_var):
        in_data = in_var.data
        output = self.forward(in_data)
        ret = Variable(output)
        ret.set_creator(self)
        self.input = in_var
        self.output = ret
        return ret

    def forward(self, in_data):
        return in_data

これらを用いて、先程のforward計算を行ったあとに最終出力Variableから後ろ向きに途中出力、途中の関数を全て辿る、というのをやってみます。

data = [0, 1, 2, 3]
x = Variable(data)

f_1 = Function()
y_1 = f_1(x)
f_2 = Function()
y_2 = f_2(y_1)

print(y_2.data)
print(y_2.creator)                           # => f_2
print(y_2.creator.input)                     # => y_1
print(y_2.creator.input.creator)             # => f_1
print(y_2.creator.input.creator.input)       # => x
print(y_2.creator.input.creator.input.data)  # => data

>>> [0 1 2 3]
>>> <__main__.Function object at 0x1021efcf8>
>>> <__main__.Variable object at 0x1021efd30>
>>> <__main__.Function object at 0x1021efcc0>
>>> <__main__.Variable object at 0x1023204a8>
>>> [0 1 2 3]

まずVariableのコンストラクタにはnumpy.ndarray形式のデータが渡されます。このVariable形式のオブジェクトxが、ネットワークへの入力になります。

f_1 = Function()

ここではネットワークの一つのレイヤとして用いたいFunctionを実体化させています。このFunctionは恒等写像で、パラメータを持たないのでコンストラクタに与えるべき情報もないため、引数はありません。

y_1 = f_1(x)

この行で関数f_1を入力データxに適用し、その出力をy_1に代入しています。出力もVariable形式となっているはずなので、y_1はVariableクラスのインスタンスです。f_1は関数として呼ぶと内部の__call__が呼び出されるので、この行ではFunctionクラスの__call__メソッドにxが渡されているということになります。それではまず__call__メソッドの中身を見ていきましょう。

in_data = in_var.data

現在のコードではなんの型チェックも走っていませんが、渡された引数はVariableであるという前提から、そのVariableのdata要素を取り出してin_dataに入れています。これが実際のforward計算に必要なデータそのものになります。

output = self.forward(in_data)

ここでは、自オブジェクトのforwardメソッドに、前行で入力Variableから取り出されたnumpy.ndarray型の配列を渡し、返り値をoutputに入れています。

ret = Variable(output)

この行では、forward計算の結果であるoutputがnumpy.ndarray型の配列であるという前提から、これを再びVariable型にくるみなおしています。このことから、forwardメソッド自体はnumpy.ndarray型の配列を受け取ってnumpy.ndarray型の配列を返す関数になっていればよいということになります。

ret.set_creator(self)

さて、次に来るこの行では、Variableにくるまれたforward結果retに対し、生成者が自分であるということを記憶させています。ここで、Variableクラスのset_creatorメソッドを見てみましょう。

def set_creator(self, gen_func):
    self.creator = gen_func

ここでは、受け取ったFunctionクラスのオブジェクトを、自身のself.creatorメンバ変数に格納しています。これによって、このVariableは自分を出力したFunctionへの参照を保持することができるわけです。

self.input = in_var

次に、このFunctionへ渡された入力Variable: in_varをself.inputに格納して保持し、のちのちここから自分より前に呼ばれたFunctionを辿っていけるようにしています。

self.output = ret

さらにself.outputにforward計算の結果のVariable: retを格納します。これは、あとでBackpropagationの際に、ひとつ上のレイヤでの勾配が必要になるためです。これは微分の連鎖律のことを考えると頷けます。参考：ロスに対するあるレイヤのパラメータについての勾配

return ret

最後に、retを返します。結果として、Functionクラスのオブジェクトを関数として呼びVariableを渡すと、中身のdataに対してforwardメソッドを適用して得られた結果を再びVariableにくるんだものが返ってくる、ということになります。

勾配の計算を行うコード (exp_2.py)

ここまでに出てきたコード中のFunctionは、パラメータを持たなかったので、更新すべきものがないネットワークしか構築できませんでした。しかし、もし何らかのパラメータによって決定づけられるような変換をFunctionのforwardが行うのだとすると、その変換を何らかの損失尺度を最小化するものにするために、パラメータの最適値を計算したくなります。Neural Networkの場合、勾配降下法をベースとした手法を用いてこのパラメータを最適化することが多く、このためには損失尺度の計算を行うロス関数に対する全パラメータについての勾配を求める必要があります。これを、多数の関数の合成写像と考えられる多層ネットワークに対して行うための手法がBackpropagationでした。

Backpropagationによる微分の連鎖律の実装は非常にシンプルなので、いろいろなやり方がありえますが、ここでは前述のVariableとFunctionの実装に基づいた、「出力Variableから逆向きに計算履歴が辿れる」ことを利用した実装方法をコードを使って説明してみます。

まずは必要な関数の定義と、forward計算です。ここではデータに二つの関数を適用したのちロス計算が行われる、というネットワークを考えてみます。

f1 = Function()  # 1つ目の関数の定義
f2 = Function()  # 2つ目の関数の定義
f3 = Function()  # ロス関数の定義

y0   = Variable(data)  # 入力データ
y1   = f1(y0)          # 1つ目の関数適用
y2   = f2(y1)          # 2つ目の関数適用
y3   = f3(y2)          # ロス関数適用

では、この最終出力Variable（y3）を基点として、データに適用された関数たちを逆順に辿りながら、各レイヤの勾配を順に計算していきます³。計算された勾配は各関数の入力Variableのgradメンバに格納します。こうすると、ある層のinput＝一つ下の層のoutputなので、一つ下の層からこの勾配が参照できるようになります。

f3 = y3.creator                      # 0. まずロスの値からロス関数を辿る

gx = f3.backward()                   # 1. ロス関数の勾配
f3.input.grad = gx                   # 2. 入力の grad に格納

f2 = f3.input.creator                # 3. 一つ下層の関数を辿る

gx = f2.backward()                   # 4. 現在のレイヤの勾配(d出力/d入力)
f2.input.grad = f2.output.grad * gx  # 5. f.inputに関するロス関数の勾配

f1 = f2.input.creator                # 3. 一つ下層の関数を辿る

gx = f1.backward()                   # 4. 現在のレイヤの勾配(d出力/d入力)
f1.input.grad = f1.output.grad * gx  # 5. f.inputに関するロス関数の勾配

5.では微分の連鎖律に従いdロス関数 / d入力 = (dロス関数 / d出力) * (d出力 / d入力)という計算をしています。また、5.までいったら、3.から繰り返していることが分かります。

このようにすると、最終出力Variableであるy3から、全てのレイヤの入力について、ロスに対する勾配を計算することができることが分かりました。またこれは、代入の際に無駄に行を分けずに、かつ分かりやすいように名前のついた形でforward計算の際に一時利用した中間出力Variableを使って短く書くと、以下のコードと同じです。

# y3を起点にして
f3 = y3.creator

y2.grad = f3.backward() * 1        # y2についてのf3の勾配 * y3についてのf3の勾配
y1.grad = f2.backward() * y2.grad  # y1についてのf2の勾配 * y2についてのf3の勾配
y0.grad = f1.backward() * y1.grad  # y0についてのf1の勾配 * y1についてのf3の勾配

さらにf3 = y3.creatorの後からを1行で書くと、

y0.grad = 1 * f3.backward() * f2.backward() * f1.backward()

となります。これはまさに以下のような微分の連鎖と対応しています。

$$
\frac{\partial \mathcal{f_3}}{\partial y_0} =
\frac{\partial \mathcal{f_3}}{\partial y_3}
\frac{\partial \mathcal{y_3}}{\partial y_2}
\frac{\partial \mathcal{y_2}}{\partial y_1}
\frac{\partial \mathcal{y_1}}{\partial y_0}
$$

y0はネットワークへの入力なのでx、f3はロス関数なのでl、y3はロスなのでlossなどと名付けるべきかもしれませんが、ここでは勾配を求めるというbackward計算が上層から下層へ同じ計算を繰り返すことで行われていることを強調するために添字だけが変わっていくような記法を採用しました。また、y3によるf3の微分とは自分自身での微分を意味するので $1$ です。

ただし、これではまだFunctionが持つパラメータを更新するのに必要な勾配を計算しきれていません。パラメータを更新するためには、ロス関数に対するパラメータについての勾配が必要です。これを得るには、各backwardメソッドの中で、まず自らの出力に対するパラメータについての勾配を計算し、それを上層から伝わってくる勾配に乗じて得られるgwを計算すればよいだけです。

例えば、途中の関数f2がパラメータwを持っており、入力y1に対してw * y1という変換を行うとすると、wについてのf2の勾配はy1であり、これはf2への入力f2.inputなので、gwは以下のようになります。

gw = f2.input.data * f2.output.grad

上層からの情報はf2.outputVariableが集約し、下層からの情報はf2.inputVariableが集約しているので、これらを用いて層内のパラメータについてのロス関数に対する勾配が計算できるようになっています。

このgwを使ってwというパラメータが更新されます。更新ルール自体は最適化手法によって様々に異なります。ネットワーク中のパラメータを巡回して更新を行うためのOptimizerについては後述します。

さて、以上のようなBackpropagationの計算過程を、最終出力Variableにbackwardというメソッドを持たせて、この中で全て行えるように、次のような機能をVariableとFunctionに追加します。

• Variable
  • gradメンバ変数を持たせる
  • backwardメソッドを追加する
    • 自分のcreatorから計算過程を逆向きに辿る
    • 途中の全てのFunctionでbackwardメソッドを呼ぶ
    • その際各Functionの入力VariableのgradにそのFunctionのbackwardの返り値を入れていく
• Function
  • backwardメソッドを追加する
    • 自らの出力に対する入力についての勾配gxを計算
    • 上層から渡されるロスに対する出力の勾配grad_outputを受け取って、gxをかけ合わせたものを返す
    • 自らの出力に対するパラメータについての勾配を計算し、grad_outputに乗じてgwを計算し、保持

具体的には、このようになります。

class Variable(object):

    def __init__(self, data):
        self.data = data
        self.creator = None
        self.grad = 1

    def set_creator(self, gen_func):
        self.creator = gen_func

    def backward(self):
        if self.creator is None:  # input data
            return
        func = self.creator
        while func:
            gy = func.output.grad
            func.input.grad = func.backward(gy)
            func = func.input.creator

class Function(object):

    def __call__(self, in_var):
        in_data = in_var.data
        output = self.forward(in_data)
        ret = Variable(output)
        ret.set_creator(self)
        self.input = in_var
        self.output = ret
        return ret

    def forward(self, in_data):
        NotImplementedError()

    def backward(self, grad_output):
        NotImplementedError()

ここで、Functionが恒等写像だけだと面白くないので、いろいろな関数を定義できるようFunctionはインターフェースの定義だけにして、実際にforwardとbackwardを持つMulというクラスをこのFunctionを継承して定義します。

class Mul(Function):

    def __init__(self, init_w):
        self.w = init_w  # Initialize the parameter

    def forward(self, in_var):
        return in_var * self.w

    def backward(self, grad_output):
        gx = self.w * grad_output
        self.gw = self.input
        return gx

これはただ初期化の際に与えられたパラメータを入力に乗じて返す関数です。backwardの中身では自身の変換の勾配とパラメータの勾配をそれぞれ求めて、パラメータの勾配はself.gwに保持しています。

これらの拡張されたVariableとFunctionを使って、forward計算を行ってみます。

data = xp.array([0, 1, 2, 3])

f1 = Mul(2)
f2 = Mul(3)
f3 = Mul(4)

y0 = Variable(data)
y1 = f1(y0)          # y1 = y0 * 2
y2 = f2(y1)          # y2 = y1 * 3
y3 = f3(y2)          # y3 = y2 * 4

print(y0.data)
print(y1.data)
print(y2.data)
print(y3.data)

>>> [0 1 2 3]
>>> [0 2 4 6]
>>> [ 0  6 12 18]
>>> [ 0 24 48 72]

関数を適用するたびに、値が各関数に与えられた初期値倍されていくのが分かります。ここで、y3.backward()を実行すると、y3から逆順にこれまで適用された関数が辿り返されて、順次各Functionのbackwardが呼ばれ、中間入出力のVariableのgradメンバ変数にその最終出力に対する勾配が入っていきます。

y3.backward()

print(y3.grad)  # df3 / dy3 = 1
print(y2.grad)  # df3 / dy2 = (df3 / dy3) * (dy3 / dy2) = 1 * 4
print(y1.grad)  # df3 / dy1 = (df3 / dy3) * (dy3 / dy2) * (dy2 / dy1) = 1 * 4 * 3
print(y0.grad)  # df3 / dy0 = (df3 / dy3) * (dy3 / dy2) * (dy2 / dy1) * (dy1 / dy0) = 1 * 4 * 3 * 2

>>> 1
>>> 4
>>> 12
>>> 24

print(f3.gw)
print(f2.gw)
print(f1.gw)

>>> [ 0  6 12 18]  # f3.gw = y2
>>> [0 2 4 6]      # f2.gw = y1
>>> [0 1 2 3]      # f1.gw = y0

forward計算を自力で書いた後、最終出力Variableのbackward()を呼ぶ、という一連の流れにおいて各オブジェクトの中で起こっていることを簡単に図にすると以下のようになります。

Link

Linkは内部でFunctionを呼んでおり、その際にFunctionが行う変換に必要なパラメータをFunctionに渡しています。それらのパラメータはLinkオブジェクトのメンバ変数として保持されており、ネットワークの学習中は、Optimizerによって更新されます。

（to be continued)

Chain

Chainは任意の個数のLinkを内部に保持することができ、これによって更新したいパラメータなどをひとまとめにしたり、大きなネットワークのわかりやすい部分単位を記述するのに役立ったりします。

（to be continued)

Appendix

Linearレイヤの基本

Neural Networkを線型変換と非線型変換の交互適用を複数含む、一つの合成写像だと強引に言ってみることにすると、これを構成する線型変換の一つとしてはアフィン変換があり得ます。ここで言うアフィン変換とは、ある実数値ベクトルを${\bf x} \in \mathbb{R}^{d_{in}}$と置いたとき、これに重み行列${\bf W} \in \mathbb{R}^{d_{in} \times d_{out}}$を乗じ、バイアスベクトル${\bf b} \in \mathbb{R}^{d_{out}}$を足すことによって行われる、幾何学的に見ると「回転・拡大縮小・剪断、そして並進」を行うような変換のことを指します。

これをLinearというNeural Networkを構成する一つのレイヤとして実装することを考えてみます。一つのレイヤは、学習可能な（trainable）パラメータを持つ場合と持たない場合がありますが、Linearレイヤが持つアフィン変換を行うための${\bf W}$と${\bf b}$というパラメータは、望ましい変換を行うものへ更新されていくため、学習可能パラメータです。

では、LinearレイヤをPythonで書かれたクラスとして表現し、

• forward計算（${\bf x}$を取り${\bf y} = {\bf W}{\bf x} + {\bf b}$を返す計算）
• backward計算（$\partial {\bf y} \ / \ \partial {\bf W}$および$\partial {\bf y} \ / \ \partial {\bf b}$を計算）
• update計算（これらの勾配を用いてパラメータ${\bf W}, {\bf b}$を更新）

を行う機能を実装してみます。

class Linear(object):

    def __init__(self, in_sz, out_sz):
        self.W = numpy.random.randn(out_sz, in_sz) * numpy.sqrt(2. / in_sz)
        self.b = numpy.zeros((out_sz,))

    def __call__(self, x):
        self.x = x
        return x.dot(self.W.T) + self.b

    def update(self, gy, lr):
        self.W -= lr * gy.T.dot(self.x)
        self.b -= lr * gy.sum(axis=0)
        return gy.dot(self.W)

このLinearクラスでは、まず、コンストラクタでLinearレイヤが持つパラメータ（${\bf W}, {\bf b}$）を平均0、標準偏差$\sqrt{2 \ / \ {\rm in\_sz}}$の正規乱数を用いて初期化しています。

self.W = numpy.random.randn(out_sz, in_sz) * numpy.sqrt(2. / in_sz)
self.b = numpy.zeros((out_sz,))

この初期化の仕方はHeNormal⁴と呼ばれます。in_szは入力サイズ、すなわち入力ベクトルの次元$d_{in}$、out_szは出力サイズ、即ち変換後の出力ベクトルの次元$d_{out}$です。

次に、__call__メソッドがforward計算に相当しており、ここで${\bf W}{\bf x} + {\bf b}$を計算しています。

self.h = x.dot(self.W.T) + self.b

出力に対するパラメータについての勾配を計算する（＝backward）ことは、Linearレイヤの場合非常にシンプルなので、上記のコードでは独立したメソッドとしては用意していません。具体的には、$\partial {\bf y} \ / \ \partial {\bf W} = {\bf x}, \partial {\bf y} \ / \ \partial {\bf b} = {\bf 1}$（${\bf 1}$ は、要素が全て $1$ である $d$ 次元のベクトル）であり、updateメソッドの中ではこれを既知のものとして用いています。下記部分の一行目、self.xの部分が $\partial {\bf y} \ / \ \partial {\bf W}$ に相当します。二行目の右辺、gy.sum(axis=0)の部分では、gy.T.dot(numpy.ones((gy.shape[0],)))と同等の計算を行っています。このうちのnumpy.ones((gy.shape[0],))の部分が $\partial {\bf y} \ / \ \partial {\bf b}$ に相当します。

self.W -= lr * gy.T.dot(self.x)
self.b -= lr * gy.sum(axis=0)

もっと勾配の計算が複雑な場合、backwardメソッドなどを用意して、各パラメータについての勾配を計算する部分がupdateとは別になっている方が良いでしょう。

パラメータの更新は、本来様々な勾配法の変種の実装⁵に対応するために更新処理の部分が抽象化されていたり、別のクラスとして切り出されているべきですが、ここでは最もシンプルな確率的勾配降下法（Vanilla SGDと呼ばれることもあるようです）を用いてパラメータ更新を行うことだけを考え、パラメータを保持するLinearクラス自体にupdateメソッドを持たせています。

updateメソッドで行われていること自体はシンプルです。まず合成関数の微分における連鎖律に従って、上層での各レイヤ出力に対する各入力についての勾配を全レイヤ分掛け合わせたものがgyとして渡されてくるので、それをこのレイヤの出力に対するパラメータ${\bf W}, {\bf b}$についての勾配に掛け合わせたものを計算しています。すると、これが目的関数に対するパラメータ${\bf W}, {\bf b}$についての勾配ということになりますので、これに学習率lrを掛けて更新量を計算し、実際にパラメータから引き算して更新を行っています。

updateメソッドは上位層から渡されたそれまでの勾配の総乗に対し、自身の出力に対する入力についての勾配${\bf W}$を乗じたものを返しています。これがさらに下の層でgyとして利用されるわけです。

Backpropagationで必要となる勾配の計算は、連鎖律のお陰で非常に実装が簡単です。各層は自身が行う変換 $f$ に対する入力 ${\bf x}$ についての勾配 $\partial f \ /\ \partial {\bf x}$ を下の層にgyとして渡し、各層でのパラメータの更新は、上の層から渡されたgyに自身の変換 $f$ に対するパラメータについての勾配を掛け合わせ、これを使って行えばよいということになります。

以上の機能が実装されたクラスを定義しておけば、任意の入出力サイズのLinearレイヤを作ることができます。Linearレイヤに値を渡すときは、オブジェクトを関数として呼び、その引数にnumpy.ndarrayオブジェクトを渡してやればよく、内部パラメータを更新するときは、上位レイヤから渡されるgyと、更新式で用いられる学習率lrをupdateメソッドに渡してやればよいということになります。

ReLUレイヤについて

上のLinearレイヤの基本についてのAppendix冒頭で、Neural Networkを強引に「線型変換と非線型変換の交互適用」を行うものと言ったので、Linearレイヤの出力には非線型変換を適用したくなります。Neural Networkでは多種多様な活性化関数と呼ばれる非線型変換が提案されています。現在最も一般的なものの一つにReLUがありますが、その非線型変換とは以下のように書けます。

class ReLU(object):

    def __call__(self, x):
        self.x = x
        return numpy.maximum(0, x)

    def update(self, gy, lr):
        return gy * (self.x > 0)

活性化関数はパラメータを持たない変換なので、updateでは何のパラメータ更新も行っていません。その代わり、自身の劣勾配を計算してgyに乗じてあげています。

データセット読み込み

Scikit-learnというライブラリを使うとMNISTデータセットのダウンロードから読み込みまでを簡単に行うことができます。

from sklearn.datasets import fetch_mldata

# MNISTデータセットの読み込み
mnist  = fetch_mldata('MNIST original', data_home='.')
td, tl = mnist.data[:60000] / 255.0, mnist.target[:60000]

# 1-hot vectorにする
tl     = numpy.array([tl == i for i in range(10)]).T.astype(numpy.int)

# シャッフル
perm   = numpy.random.permutation(len(td))
td, tl = td[perm], tl[perm]

Validationデータも同様に作成しました。

vd, vl = mnist.data[60000:] / 255.0, mnist.target[60000:]
vl = numpy.array([vl == i for i in range(10)]).T.astype(numpy.int)

Softmax Cross Entropyの計算と微分

ネットワークの出力を ${\bf y} \in \mathbb{R}^{d_{l}}$ としたとき、Softmax関数を用いて確率ベクトルに変換したものを $\hat{\bf y}$ とおくと、これは以下のように計算されます。

$$
\hat{y}_{i} = \frac{\exp(y_i)}{\sum_j \exp(y_j)} \hspace{1em} (i=1,2,\dots,d_l)
$$

このとき、$\hat{y}_{i}\ (i=1,2,\dots,d_l)$ は確率を表すので $0 \leq \hat{y}_{i} \leq 1$ となります。

さて今、教師信号が同じく $d_l$ 次元のone-hotベクトル（要素のうち一つだけが $1$ で、その他の全ての要素は $0$ となっているようなベクトル）${\bf t} = [t_1, t_2, \dots, t_{d_l}]^{\rm T}$ で表されるとすると、$\hat{\bf y} = {\bf t}$ である尤度 $L(\hat{\bf y} = {\bf t})$ を以下のように定義できます。

$$
L(\hat{\bf y} = {\bf t}) = \prod_i \hat{y}_i^{t_i}
$$

$t_i$ は $i$ が正解のクラスのインデックスであるときだけ $1$ で、ほかは全て $0$ なので、正解のクラスが仮に $i = 5$ だとすると、上式は $1 \cdot 1 \cdots \hat{y}_{5} \cdots 1 = \hat{y}_{5}$ を表します。つまり、この $L$ は、「正解をどのくらいきちんと高い確信度を持って正解だと予測できたか」ということを意味していると解釈することができます。すると、この値を大きくすることができればよいということになりますが、一般的にはこの $L$ の対数をとり、符号を反転したもの $-\log(L)$ を最小化します。$\log$ は単調増加なので $\log(L)$ が最大のとき $L$ も最大となり、また $\log(L)$ が最大のとき符号を反転させた $-\log(L)$ は最小となるはずです。結果的に $-\log(L)$ を最小化することで上式で表している尤度を最大化していることになります⁶。この $-\log(L)$ は尤度の対数を取って符号を反転させたので「負の対数尤度」と呼ばれますが、Neural Networkの文脈ではクロスエントロピーと呼ばれることの方が多いように思います。さて、このクロスエントロピーをこれを改めて $\mathcal{L}$ と置くと、

$$
\mathcal{L} = - \log \prod_i \hat{y}_i^{t_i} = - \sum_i t_i \log \hat{y}_i
$$

です。これを分類問題を解くNeural Networkを学習するためのロス関数として用い、最小化を目指すことになります。

さて、上述のようなPythonクラスを用いたレイヤの定義において、「常にupdateメソッドのgyには $1$ が渡される」とすればロス関数を一つのレイヤとして考えることができます。ロス関数自体は更新すべきパラメータを持たないので、updateメソッドで行うべき計算は出力＝ロスの値に対する「ロス関数への入力＝ネットワークの出力」についての勾配を求めること、となります。つまり、以下です。

$$
\frac{\partial \mathcal{L}}{\partial {\bf y}}
$$

すなわち、以下を計算すればよいと分かります。$k=1,2,\dots,d_l$ について、

$$
\begin{eqnarray}
\frac{\partial \mathcal{L}}{\partial y_k}
&=& - \sum_i \frac{\partial \mathcal{L}}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial y_k} \\
&=& - \sum_i \frac{t_i}{\hat{y}_i} \frac{\partial \hat{y}_i}{\partial y_k} \hspace{1em}\cdots(1)
\end{eqnarray}
$$

ここで総和記号がはずれないのは、Softmax関数は分母に全ての次元の値を持つため、全ての添字に対する関数になっているからです。さて、そのSoftmax関数の勾配は、

$k \neq i$のとき
$$
\begin{eqnarray}
\frac{\partial \hat{y}_i}{\partial y_k}
&=& -\frac{\exp(y_i)\exp(y_k)}{\sum_j \exp(y_j)} \\
&=& - \hat{y}_i \hat{y}_k
\end{eqnarray}
$$

$k = i$のとき
$$
\begin{eqnarray}
\frac{\partial \hat{y}_i}{\partial y_k}
&=& \frac{\exp(y_i)}{\sum_j \exp(y_j)}

• \frac{\exp(y_i)\exp(y_k)}{\left\{ \sum_j \exp(y_j) \right\}^2} \\
  &=& \hat{y}_i(1 - \hat{y}_k) = \hat{y}_k(1 - \hat{y}_k)
  \end{eqnarray}
  $$

となることから、これを用いて$(1)$ 式を、総和記号の中身が $i = k$ のときと $i \neq k$ のときで別々の項に分解できることに注意して変形していくと、

$$
\begin{eqnarray}
\frac{\partial \mathcal{L}}{\partial y_k}
&=& - \sum_i \frac{t_i}{\hat{y}_i} \frac{\partial \hat{y}_i}{\partial y_k} \\
&=& - t_k (1 - \hat{y}_k) + \sum_{i \neq k} t_i \hat{y}_k
\end{eqnarray}
$$

となります。ここで、第1項が $i = k$ のとき、 第2項が $i \neq k$ のときです。さらに変形していくと、

$$
\begin{eqnarray}
&=& - t_k + \hat{y}_k t_k + \hat{y}_k \sum_{i \neq k} t_i \\
&=& - t_k + \hat{y}_k \sum_i t_i \\
&=& \hat{y}_k - t_k
\end{eqnarray}
$$

となります。ここで、最後の変形にはone-hotベクトルの性質（$\sum_i t_i = 1$）を用いています。結果を再度ここに書き直すと、

$$
\frac{\partial \mathcal{L}}{\partial y_k} = \hat{y}_k - t_k
$$

であることが分かりました。つまり、これがSoftmax Cross Entropyクラスのupdateメソッドから返ってくるgyだというわけです。

ロスに対するあるレイヤのパラメータについての勾配

ロス関数を $\mathcal{L}$ とおくと、第 $l$ 層のパラメータ ${\bf W}_l$ についてのロス関数の勾配は、その上層のレイヤを $l+1, l+2, \dots, L$ として、微分の連鎖律により以下のようになります。

$$
\frac{\partial \mathcal{L}}{\partial {\bf W}_l} =
\frac{\partial \mathcal{L}}{\partial y_L}
\frac{\partial y_L}{\partial y_{L-1}} \cdots
\frac{\partial y_{l+1}}{\partial y_l}
\frac{\partial y_l}{\partial {\bf W}_l}
$$

このとき $\partial y_{l+1}\ /\ \partial y_l$ から $\partial y_{L}\ /\ \partial y_{L-1}$ までの各勾配は全て、第 $l$ 層につながる上位のレイヤの出力に対する入力についての勾配になっています。これを入出力勾配と名付けてみます。すると最後の $\partial \mathcal{L}\ /\ \partial y_L$ についても、$\mathcal{L}$ を第 $L+1$ 層のロスレイヤと考えれば同様で、ロスレイヤの出力（ロス）に対する入力（ネットワークの予測値）についての勾配なので入出力勾配です。つまり、自らの層とロスの間をつなぐ各層の入出力勾配を全てかけ合わせたものに、自らの層の出力に対するパラメータについての勾配を掛け合わせたものがbackward計算で計算したいものなので、各レイヤの入出力勾配を、自分にVariableを渡してきた全てのFunctionに渡してやり、渡された側はそれに自分の入出力勾配を掛け合わせたものをさらに下の層に渡してやる、ということをやればよいということになります。

1. 関連したPRとしては次のものがあります。 "Support advanced indexing with boolean array for getitem": https://github.com/pfnet/chainer/pull/1840 ↩

2. 予め条件分岐先の数が分かっている場合は、全ての分岐先のネットワークを予め定義しておき、それらを分岐点で切り替えてforward計算を行えばよいので、Define-and-Runでも実現することができます。しかし、分岐点で分岐が発生したときに初めて分岐先のネットワークをデータに依存したなんらかの量などに基づいてその場で定義したい場合などは、Define-and-Runでは構築がそもそも不可能になります。あらかじめあらゆるデータに対応した分岐先のネットワークを定義しておくことはできないからです。 ↩

3. 正確にはロス関数に対する各レイヤの入力Variableについての勾配のこと。 ↩

4. He et al., "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification", http://arxiv.org/abs/1502.01852 ↩

5. ChainerではAdaDelta, AdaGrad, Adam, MomentumSGD, NesterovAG, RMSprop, RMSpropGraves, SGD (=Vanilla SGD), SMORMS3が実装されています。RPropはなく、EveはPRが出ています（ https://github.com/pfnet/chainer/pull/1847 ）がまだマージされていません。早くアダムとイブを揃えてあげたいですね（？）。 ↩

6. 別の導出としてはKLダイバージェンスを用いたものなどがあります。Chainer Playgroundで行われている解説などがそうです。 https://play.chainer.org/book/1/1/11 ↩