この記事は WebAudio Web MIDI API Advent Calendar 2016 の21日目です。
※ μ-Lawの表記など誤りがあったので訂正しました(2017.03.14)
あらすじ
WebAudio の ScriptProcesser を使って原始的な手法で音声の圧縮を実験してみたところ、現代の音声圧縮コーデックのMP3やAACの凄さを思い知りました。
WebAudioのデータ量
WebAudioで音声をデータとして取得するには、ScriptProcessorを使いますよね。その時の1秒当たりのデータ量はどれくらいでしょうか?
サンプルリングレート
まずサンプリングレートを確認してみましょう。
var ctx = new window.AudioContext();
console.log(ctx.sampleRate);
実行してみたところ、環境によって異なることが分かりました。
- Windows 7
- Chrome 55 ... 48000
- Firefox 50 ... 48000
- MacOS X 10.12
- Chrome 55 ... 44100
- Firefox 50 ... 44100
- Chrome OS 54
- Chrome 54 ... 48000
Windowsは1秒間に4万8千個のサンプル数(48kHzでサンプリング)、Macは4万4100個のサンプル素(44.1kHzでサンプリング)していることになります。
CDが44.1kHz, (使ったことはないですが)DATが48kHzなので、同じくらい。音楽用としてはまずまずですね。
ちなみにいわゆるハイレゾ音源は96kHz以上を言うようなので、WebAudioはサンプリングレートから見るとハイレゾの範疇には入らなそうです。
量子化
1サンプルをどれぐらい細かく表現できるかという、量子化も重要です。他の規格では次のようなリニア(均一な)量子化が行われていいます。
※参考: 藤本健のDigital Audio Laboratory 第572回:ハイレゾで注目の「32bit-float」で、オーディオの常識が変わる?
- CD / DAT ... 16bit整数、65,536段階
- ハイレゾ音源 .... 24bit整数、16,777,216段階 (か、それ以上)
対してWebAudioでは次のように実数が利用されています。
- WebAudio ... -1.0 ~ 1.0 の32ビット実数
- ※注意:-1.0 ~ 1.0の範囲だと思っていたのですが、実際に発生するデータはその範囲を超える様です。正しい仕様をご存知の方は、ぜひ教えてください。
実数を使っているのでリニア量子化ではなく直接比較は難しいのですが、ダイナミックレンジ(音の大小の表現の幅)では24bit整数をはるかに超えます。こちらはハイレゾ音源の資格は十分満たしていると思います。
1秒当たりのデータ量
ここで、1秒当たりのデータ量を計算してみます。話をシンプルにするために、モノラル音声で考えてみましょう。
- Windowsの場合(48kHz) ... 48,000 * 32 = 1,536,000 bit/sec = 192 KB/sec ≒ 1.5Mbps
- Macの場合(44.1kHz) ... 44,100 * 32 = 1,411,200 bit/sec = 176.4 KB/sec ≒ 1.4Mbps
なかなかのデータ量です。もしリアルタイムで送ろうとしたら、3G携帯ではギリギリです。
音声データの圧縮
圧縮には情報が維持される可逆の方式と、情報が一部失われる非可逆の方式があります。画像でいうとPNGは可逆、jpegは非可逆ですね。音声ではFLACやApple Loss Lessが可逆、MP3やAACなどは非可逆の圧縮方式です。
今回は音楽ではなく人の声を想定して、乱暴な非可逆圧縮をやってみましょう。(この先はMacの44.1kHzの場合で計算します)
サンプリングの間引き
まず、簡単な方法としてサンプリングレートを下げる、つまり音声サンプルを間引いて半分にします。
44kHzのサンプリングなら、その半分の22kHzの音を表現できると言われています。半分の22kHzならば11kHzまでです。昔ながらの固定電話が3.4kHzまでということなので、11kHzであれば十分に人の声を伝えられそうです。
ビット数の削減
次に1サンプルあたりのビット数も減らしましょう。CDを見習って、16bitの整数にしてしまいましょう。これでまたデータ量が半分になります。
// サンプルの間引きと16bit整数化
function _convertoFloat32ToInt16(srcArr) {
// srcArr: 32bit実数の配列
let l = srcArr.length;
let arr = new Int16Array(l/2); // 16bit整数配列、サンプル数を半分に
while (l--) {
if(l%2==0){
arr[l/2] = srcArr[l]*0x7FFF;
}
}
return arr;
}
ここまでの圧縮効果
- 元(44.1kHz, 32bit実数) ... 1,411,200 bit/sec = 176.4 KB/sec ≒ 1.4Mbps
- 後(22.05kHz, 16bit整数) ... 352,800 bit/sec = 44,100 KB/sec ≒ 350Kbps
元の1/4まで小さくなりました。3Gの携帯回線でも、十分リアルタイム送信できそうです。
さらなる圧縮
ここでもう一段、圧縮したいところです。サンプルを8bitまで落とせば、元の1/8となります。単純に8bit整数のリニア量子化では粗くなってしまいますが、ここでμ-Lawというアルゴリズムを使ってみましょう。このアルゴリズムはG.711という音声コーデックで使われているそうです。
対数表現を使うことで、小さい音は細やかに、大きな音はおおざっぱに表現して、S/N比(Signal - Noise 比)を改善しています。
ここまでやると、データ量を元の1/8まで減らすことができます。
- μ-Law方式(22.05kHz, 8bit整数) ... 176,400 bit/sec = 22.05 KB/sec ≒ 176 Kbps
圧縮のコード
// -- サンプルの配列をμ-Law圧縮する --
function _compressAudio(srcArr) {
// srcArr: 32bit実数の配列
let mu = 127; // -127〜127の整数で表現する
let alpha = 1.0 / Math.log(1 +mu) * mu; // 定数を計算しておく
let l = srcArr.length;
let arr = new Int8Array(l/2); // 8bit整数、サンプル数を半分に減らす
for (let i = 0; i < l; i +=2) { // 1つおきに取り出す
let s = srcArr[i];
if (Math.abs(s) > 1.0) {
console.warn('signal TOO big s=' + s);
}
let n = _muLaw(s, mu, alpha); // 実数のまま計算
arr[i/2] = n; // ここで整数に丸める
}
return arr;
// -- 各サンプルをμ-Law圧縮する --
function _muLaw(s, mu, alpha) {
let sign = Math.sign(s);
let absS = Math.abs(s);
let n = sign * Math.log(1 + mu*absS) * alpha;
return n;
}
}
復元のコード
// -- サンプルの配列をμ-Lawで復元する --
function _decomressAudio(srcArr) {
// srcArr: 8bit整数の配列
let mu = 127; // -127〜127の整数で表現されている
let mui = 1.0 / mu; // 定数を求める
let l = srcArr.length;
let arr = new Float32Array(l*2); // 32bit実数、サンプル数を倍に増やす
for (let i = 0; i < l; i++) {
let n = srcArr[i];
arr[i*2] = _invMuLaw(n, mu, mui);
// 抜けているサンプルを、前後のサンプルの平均を取って推定する
if (i > 0) {
arr[i*2 -1] = (arr[i*2] + arr[i*2 -2]) / 2.0;
}
}
arr[l*2 -1] = arr[l*2 -2]; // 最後のサンプルは一つ前の繰り返しで近似
return arr;
// 各サンプルをμ-Lawで復元する
function _invMuLaw(n, mu, mui) {
let sign = Math.sign(n);
let absN = Math.abs(n);
let f = absN * mui;
let s = sign * mui * (Math.pow(1+mu, f) -1);
return s;
}
}
目で見てみよう
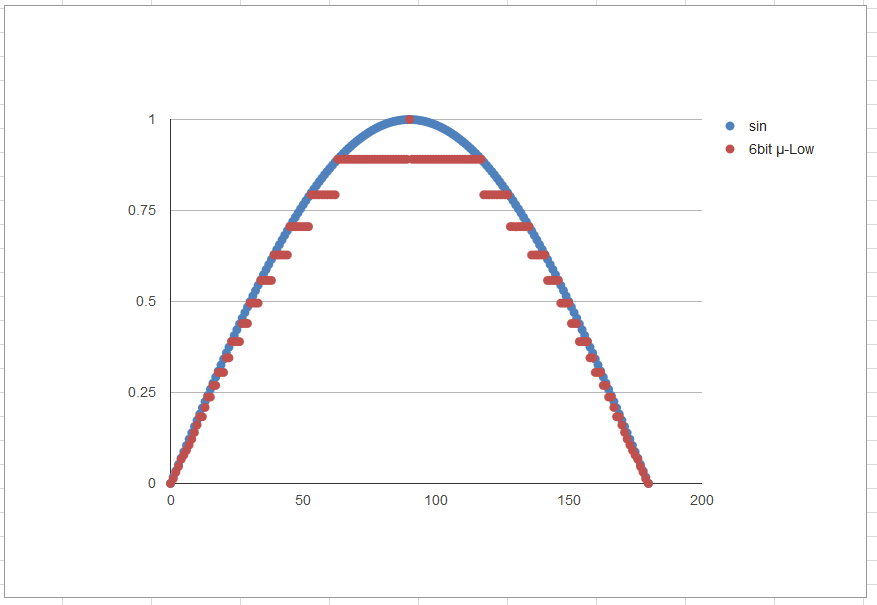
μ-Lawのアルゴリズムを視覚的にとらえられるように、サイン波を圧縮→復元してみた様子をプロットしてみました。
6bit符号付き(-31~31)
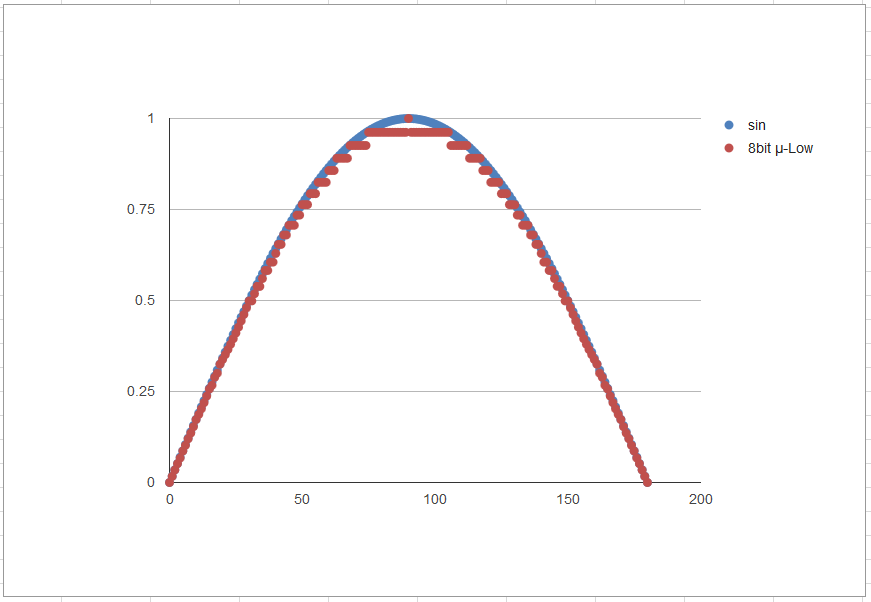
8bit符号付き(-127~127)
6bitではかなり粗いですが、8bitなら見た目は良好です。果たして耳ではどうでしょうか。
聴いてみた感想
こちらの「WebAudioでなんちゃってWebRTCする」を参考にしてコードを組み立てます。そして自分の声と耳で聴いてみました。
- navigator.mediaDevices.getUserMedia()でマイクの音を取得
- AudioContext.createMediaStreamSource()でMediaStreamAudioSourceNodeを生成
- band-pass フィルターをかける(こちらの「雑音を雑にカットする」を真似ました)
- AudioContext.createScriptProcessor()でScriptProcessorNodeを生成、音声をサンプリング
- 8bit μ-Lawで圧縮
- 8bit μ-Lawから復元
- AudioContext.createBuffer()でAudioBufferを生成、復元したデータをセット
- AudioContext.createBufferSource()でAudioBufferSourceNodeを生成、AudioBufferの内容を再生
主観的には、PC内蔵マイクで取得した人の声なら違和感なく聞けそうです。
サンプル
GitHub Pages でも公開しておきます。お試しになる場合は、ハウリングしないようにヘドフォンをご利用ください。
- GitHub Pages で試す https://mganeko.github.io/webrtcexpjp/tool/mulow.html
- GitHubでソースを見る https://github.com/mganeko/webrtcexpjp/blob/master/tool/mulow.html
まとめ
最後に、今回の方式と現代的な音声圧縮との比較を行ってみます。
- 今回のμ-Law方式(22.05kHz, 8bit整数) ... 176,400 bit/sec = 22.05 KB/sec ≒ 176 Kbps
- MP3 よくあるPodcast ... 64 Kbps
- AACの高音質音楽 ... 192 ~ 256 Kbps
MP3なら今回の方式の半分以下のデータでとてもクリアな人の声が伝えられます。AACなら同程度のデータで音楽として十分な表現力を持っています(しかもステレオ)。技術の進歩は凄いですね。コーデック開発に関わっている人たちに、感謝します。
もちろん、この記事を読んでいただいたあなたにも、ありがとうございます!