Importance Weighted Autoencoders
最近、深層生成モデルに興味あるのでICLRにも採択されていたIWAE(Importance Weighted Autoencoders)の実装をTensorFlowで行いました。ついでにBengio達の書いたDeepLearning本の20章(Deep generative models)を一部まとめました。
深層生成モデルとは?
深層生成モデルが何かと言われる難しいですがおそらくNeural Networkを使った生成モデルです。
Bengio本にも書かれていますがDeepLearningの中でも最重要研究の一つです。実際、DeepLearning系の国際会議ICLRにも結構それ系の話が出ています。
例えば深層生成モデルを使うと下のようなことができます。具体的には例えばだんだん元の数字に対して0を足しこんでいくということができるようになります。(下の画像は上の行が元の(reconstructした)数字でだんだん行が下がるにつれ0の成分を足しこんでいったものです)

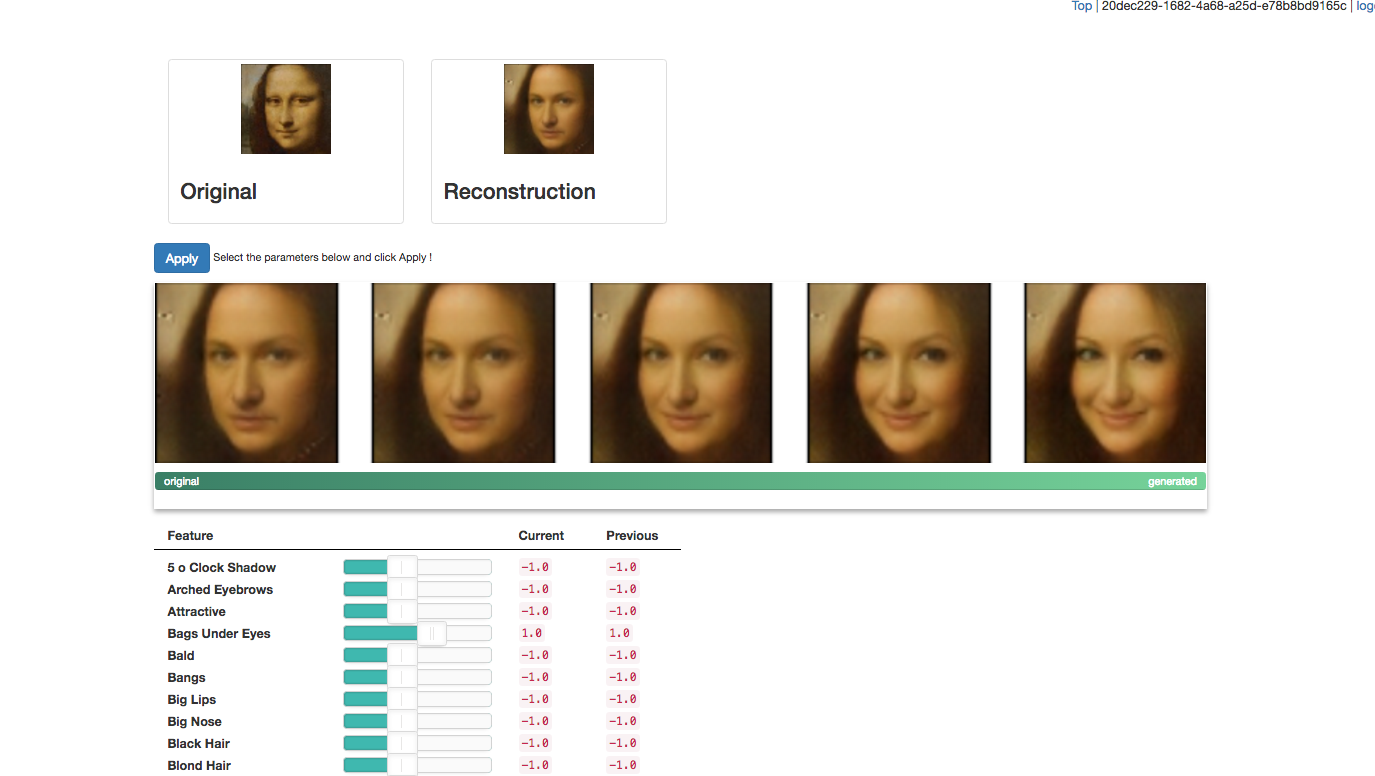
日頃生成モデルのことも含めて色々教えて頂いている先輩が作ったものを使うと次のようなことも出来ます。(http://deeplearning.jp/suzuki/ のDemoのところから遊ぶことができます。)
今回はモナリザの画像に右にいくにつれSmiling成分と女性成分を加えていっています。他にも色々な成分を加えることができます。肖像権的な問題が不安なので今回はモナリザにしましたが自然画像で色々やると遊べて楽しいです。
最近の深層生成モデルの二(三?)大柱
深層生成モデルの基本となる二大柱としてVAE(Variatioinal Autoencoder)とGAN(Generative Adversarial Nets)があります。少々、言い過ぎかもしれませんが最近の深層生成モデルの研究の大体がこれらと関係していると言っても過言ではないくらい重要なものです。もう一つ全然違う考え方の生成モデルとしてGMMがあります。
Boltzmann machineは...?ってなっている方もいるかもしれませんが対数尤度を見ると上の3つの方がいいので最近は(自分の知る範囲内では)あまり研究はされていない気がします。
ここではBengio達のDeep learning本に沿ってその3つに関して簡単に個条書きしていきます。
また自分が日頃色々教えて頂いている先輩の書いたパワポとかが文献[2]にあるのでそれも概要を掴むのにお勧めです。とりあえずこの説明だけを読んでも分からない可能性が高いので参考文献達を色々読んだり実装すると理解が深まると思います。
VAE
原論文(https://arxiv.org/abs/1312.6114 )がとても丁寧に書いてあるのでそちらを読むことをお勧めします。基本的には従来の変分推論をBlack boxにまたLarge scaleにするというモチベのもとNeural network(=自動微分)を持ちこんだという感じです。
また変分推論は以前の記事(http://qiita.com/masasora/items/900a8d801c5b507d4583) に書いてあるのでそちらもお勧めです。あとVAEとかはあまり触れられていないですがBleiの変分推論のreview 文献[6]も最高なのでお勧めです。
今回は先ほども言った通り説明はBengio本に沿ってしますがDeep mindの人の書いた文献[13]とか本人達が書いた文献[4]も参考になります。
- $x$を入力変数、$z$を潜在変数とする。
- まず$x$から$z$を生成するencoder $p(z|x)$を用意する。このencoderをnetworkで作る。(このencoderを推論モデルともいう、作り方の詳細は後で)
- $p_{model}(z)$という分布から$z$を生成しさらに$q(x|z)$で$x$を生成することを考える。つまり事後確率を近似するdecoderとしてのnetwork $q(z|x)$を用意する。(このdecoderを生成モデルともいう)
- このとき
$L(q)=E_{z\sim q(z|x)} [\log p_{model}(z,x)] + H(q(z|x))$
と$L(q)= E_{z\sim q(z|x)} \log p_{model}(x|z) - D_{KL}(q(x|z)||p_{model}(z))$としたとき$L(q) \leq \log p_{model}(x)$
が成立する。(イエンセン使ってる ) この下限L(q)をどんどん大きくしていく。 - 上の第1式の第1項にはencoder(inferencee network)を使って潜在変数を推定して同時分布を最大化しようという心がある。第2項にはencoderの出力の乱雑さを増やしたいという心がある。
- 上の第2式の第1項にはautoencoderのreconstruction errorの心がある. 第2項にはencoder(事後確率)をpriorに近づけたいという(正則化項的な)心がある。これには$p(z)$に近づけるということはnoiseがのるという意味でそれでも復元できるようなautoencoderにしたいということである。
- 同時に第2式の第2項にはtraining phaseが終わった後のgenerative phaseにおいてのミスマッチを減らしたいという心もある。
- 19章の変分推論と違ってparametricなzを推定するencoderを導入したことがポイントである。
- 元の論文では平均$\mu$と分散$\sigma$をneural netwrokにして$z_{i}=\mu_{i}+\sigma_{i}\epsilon$($\epsilon\sim N(0,1))$となるようなencoderを使っている. (reparametrization trick) $ (\mu_{i}$と$\sigma_{i}$をNeural netにする。)一方、DecoderとしてはBernouli分布やGauss分布を使っている.
- 第2式の第一項(KL divergenceの項)は解析的に計算できる。第二項のreconstruction errorもzを何回か発生させることでMontecalro法で求めることができる。
- とてもエレガントな手法だが生成された画像がぼやけて見えることが欠点
- 理由としてはKL divergenceの項がおかしなデータにも順応させてしまうことやDecoderの部分が単純なことが原因とされている。
- 時系列versionとしてDRAW modelがある。imageをpatchに分割してだんだん書きこんでいく(attention)を使っている。
- VAEの変形versionとしてIWAE(importance weighted autoencoder)がある。変分下界がサンプリング回数を増やすごとに単調増加していくように下界の式を変えたもの。(後で詳しく説明)
GAN
DCGANとしておそらく日本でも結構有名?なやつ(文献[9])です。これも元論文(http://arxiv.org/abs/1406.2661 )を読むことをお勧めします。
- zからxを生成するgenerator network $x = g(z;\theta ^{(g)})$, discriminator network $d(x;\theta ^{(d)})$を使う。
- Genetaorは$z$から本当の分布に近いようにサンプルを生成する。
- Discriminatorは本当の分布とgeneratorからの分布を見分けるように学習する.
- その心から
$g =\arg min_{g} max_{d} v(g,d) , v(\theta_{g},\theta_{d})= E_{x\sim p_{data}}[log d(x)]+E_{x\sim p_{model}}[log (1-d(x))]$
を解くことになる。 - 問題点として最適化がかなり難しいことがある。
- 逆畳み込みを使ったDCGAN、差分ごとに学習していくLAPGANなどの発展系もある。
GMM
(http://arxiv.org/abs/1502.02761 )が元論文です。
- GANやVAEなどと違って生成モデル以外を使用しない。
- モーメントを一致させていくという手法(momentが定まれば確率分布も定まる) 一見、不可能そう。なぜなら2次モーメントだけでもデータ点の二乗order個あるから。(あとで解決策を書く)
- VAEの良くない所として生成モデルの最終層がGaussian(or Beronuli)ということがあった。Gaussianは2次モーメントまでで定まってしまうので複雑な分布となり得ない。ちなみにGANはdynamicなdiscriminatorのおかげで高次元のモーメントも調整できていた。
- Generative Moment Matching NetworksはMMD(maximum mean discrepancy)を使って密度を合わせていく。MMDとは無限次元での特徴空間に写像したときの1次モーメントを合わせる手法である。(正確に言うと再生核ヒルベルト空間上で一次モーメントを合わせる手法、MMDは別にこのシチュエーションに限らず密度比推定の文脈で以前から使われていた。)
- Autoencoderと組み合わせて使う。というか組み合わせて使わなければ使えない。
- GANに対する欠点としてGMMNはデータを一つずつ入れていけないということがある。なぜならモーメントを計算するのに経験分布を使うので一気にどばって入れなければならないから。
Tips
Neural network全般に言えることですが最適化のときはbatch normalizationを使ったほうが精度も収束速度も上がります。また画像のときはDecoder部分に逆畳み込み入れたほうがいいです。
IWAEとは?
普通のVAEではKL divergenceの項が分けられるので分けていました。しかし分けないで直接モンテカルロ法でサンプリングすることもできるはずです。このとき、普通にサンプリングすると重みは$1/n$になりますがimportance weightedになっているのがIWAEです。サンプリング回数を増やしていくと下界が上がっていくということが知られています。(証明もそんなに難しくはないです。)
詳しくは論文( https://arxiv.org/abs/1509.00519 )を参考にしてください。
VAEとは
$L(q)=E_{z\sim q(z|x)} [log \frac{p(z,x)}{q(z|x)}]$
$L(q)= E_{z\sim q(z|x)} \log p(x|z) - D_{KL}(q(x|z)||p(z))$
という下界を上げていく手法でした。後者の式の方が解析的に解ける部分が出ていてサンプリングする部分が減っているのでいい気がしますがとりあえず前者の式で考えてみます。
この式は
$L(q)=E_{z^{(1)},..z^{(k)} \sim q(z|x)} [\frac{1}{k} \sum log \frac{p(z,x)}{q(z|x)}]$
と書いても構わないことがすぐに分かりますがIWAEでは
$L(q)=E_{z^{(1)},..z^{(k)} \sim q(z|x)} [\sum \frac{1}{k}\log \frac{p(z,x)}{q(z|x)}]$
を使います。実際にモデルエビデンスの下界になっていることが分かります。先ほども書いた通り重要な性質としてkを増やすと下界が上がっていくということがあります。
このままだと使えないですが下のようにすると使えます。
$E_{z^{(1)},..z^{(k)}\sim q(z|x)}[\sum \tilde{\omega_{i}} \nabla _{\theta} \log \omega _{i} (x)]$
$\omega$は$\frac{p(z,x)}{q(z|x)}$です。また$\tilde{\omega_{i}}$は$\omega$を規格化したものです。この式を見るとimportance weightedの意味が分かると思います。
実際の実装
Codeは自分のgithub(https://github.com/Ma-sa-ue/practice/tree/master/generative_model) にあげています。
普通のVAEの良い実装が文献[14]に上がってるのでそれを改良しています。
具体的にはサンプリング回数を増やせるようにして、batch normalizationを加えてIWAEにしています。(batch normalizationの効果も絶大です。)
下がIWAEでreconstructした画像です。(左がtest画像、右がreconstructした画像です)
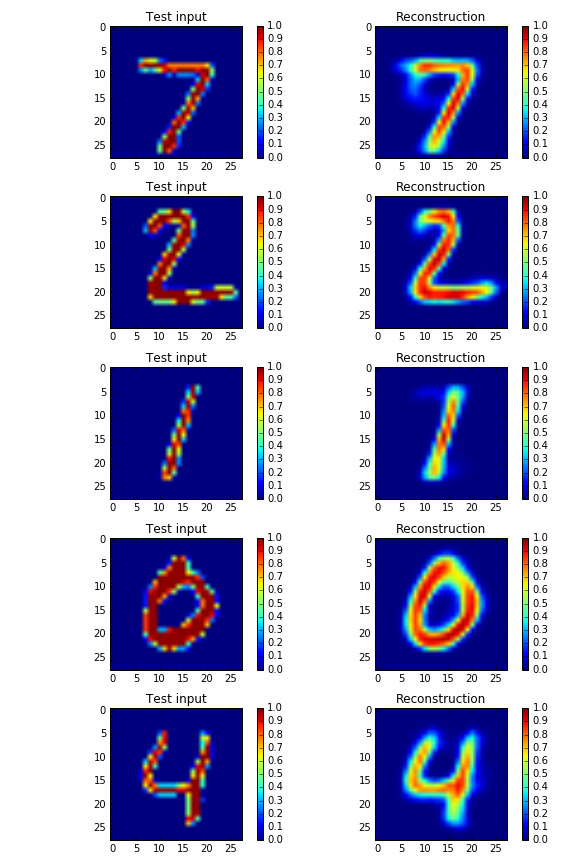
実際、普通のVAEと比べると生成モデルとしては負の対数尤度もかなり下がっていてこちらのほうが生成モデルとしてはよいということも定量的に分かります。
これからの生成モデル
(深層)生成モデルの研究はさかん(?)で半教師、時系列の状況下での研究とこもあります。またGaussian processと組み合わせたりしているグループもあります。またStanにその枠組みを組み込んでいる某グループもあります。これからどうなるかは正直全然予測できないですが、一つ確かなことは研究速度がかなり速いので、研究している人達が大変になっていくということでしょうか...
参考文献
-
http://www.deeplearningbook.org/
Bengio達のDeep learning本 - http://deeplearning.jp/workshop/ 松尾研の輪読資料 生成モデルの輪読資料が結構上がっている。
-
https://arxiv.org/abs/1312.6114
VAEの元論文 -
https://ift6266h15.files.wordpress.com/2015/04/20_vae.pdf
VAEの分かりやすい本人達による(?)説明 -
http://www.shakirm.com/papers/VITutorial.pdf
DEEP MINDの人の書いた変分推論に関する分かりやすい資料 -
http://arxiv.org/pdf/1601.00670v2.pdf
Bleiの書いた変分推論の非常に有益なReview。書いてあることはVAE以前の変分推論の話だがいわゆる混合Gauss分布などをconjugate exponential familyとして統一的な視点で変分推論の枠組みを説いている。 - http://arxiv.org/abs/1406.2661 GoodfellowによるGANの論文
- http://evjang.com/articles/genadv1 GANのわかりやすいtutorial
-
http://qiita.com/mattya/items/e5bfe5e04b9d2f0bbd47
PFNの人の書いたGANの記事 - http://arxiv.org/abs/1502.02761 GMMの論文
- https://jmetzen.github.io/2015-11-27/vae.html VAEのわかりやすい実装
-
http://www.slideshare.net/beam2d/learning-generator
PFNの人の書いたとてもためになる生成モデルに関するパワポ - http://qiita.com/masasora/items/900a8d801c5b507d4583 自分の書いたBengio本の19章のまとめ
- https://jmetzen.github.io/2015-11-27/vae.html VAEの分かりやすい実装 今回の実装はこの実装を元にした
- https://arxiv.org/abs/1509.00519 IWAEの論文
- http://fvae.ail.tokyo/ 研究室の先輩が作った顔画像生成のDemoがある 色々遊ぶと面白い