今回の内容
順伝播型ネットワーク
深層学習が成り立つ仕組み、問題に対するアプローチについて簡単に触れます。
はじめに
最近、深層学習について興味があって、理解した内容を書いていこうと思います。
今回の教科書は深層学習という本で勉強します。教科書を丸っきり一緒のことは書かないです。
この本の内容は大きく分けて以下のものがあります。
- 順伝播型ネットワーク
- 確率的勾配降下法
- 誤差逆伝播法
- 自己符号化器
- 畳込みニューラルネット
- 再帰型ニューラルネット
- ボルツマンマシン
順番にメモを書いていきます。今回は順伝播型ネットワークをメモを書きます。
1. 順伝播型ネットワーク
1.1 順伝播型ネットワークについて
順伝播型ネットワークとは、情報が入力側から出力側に一方向にのみ伝搬させていくネットワークのことです。
(他の文献では多層パーセプトロンともいうみたいです。)
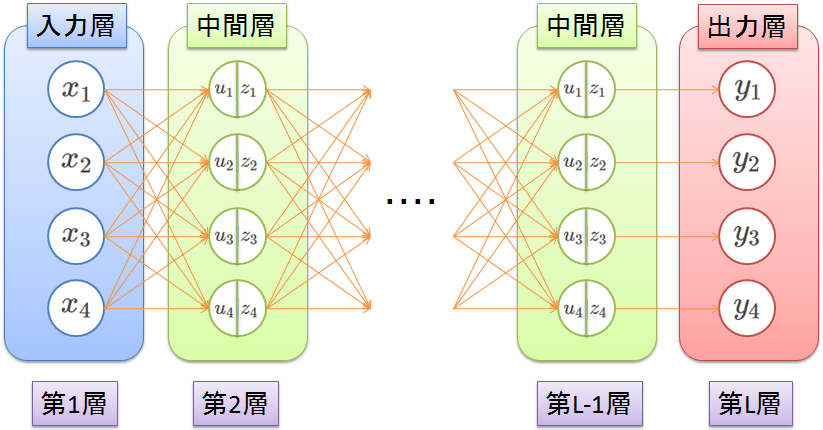
下の図は入力が4個あって、出力も4個です。別に入力数と出力数が異なっていてもよいです。
(例えば、色んな手書きの数字を入力にして、0~9の数字の評価を行なうってのは入力がN個で出力が10個だったりします。)
丸の一つ一つが何らかの情報を表しており、これをユニットといいます。
また、入力層、出力層、中間層はそれぞれ、
入力のユニットの集まりの層、最終結果のユニットの集まりの層、入力層と出力層の間の層
となっています。(中間層は隠れ層ともいうみたいです。)
中間層にあるユニットは、一つ前の層の情報を使って、新しい情報$u$を生成し、活性化関数$f$に$u$を与えてユニットの出力$z$を作り出します。
1.2 ユニットの出力
さて、新しい情報$u$の生成の仕方ですが、
このネットワークは第1層から第2層、第2層から第3層・・・というように伝搬していきます。
伝搬させるときに情報に重みをつけて伝搬させていきます。
上の図ではオレンジの線に対して重みがのっている感じです。
例えば、第1層から第2層への伝搬を考えると、$u_1$は$x_1$の情報と$x_2$の情報、$x_3$の情報、$x_4$の情報と入力に依存しない微調整できるバイアス$b_1$で出来ています。
それぞれに対する重みを$w_{11}, w_{12}, w_{13}, w_{14}$とするとユニット$u_1$は以下のように算出されます。
u_1 = w_{11} x_1 + w_{12} x_2 + w_{13} x_3 + w_{14} x_4 + b_1
これを$u_2, u_3, u_4$も同様に計算してあげると以下のように表現できます。
u_2 = w_{21} x_1 + w_{22} x_2 + w_{23} x_3 + w_{24} x_4 + b_2\\
u_3 = w_{31} x_1 + w_{32} x_2 + w_{33} x_3 + w_{34} x_4 + b_3\\
u_4 = w_{41} x_1 + w_{42} x_2 + w_{43} x_3 + w_{44} x_4 + b_4
活性化関数$f$に$u_1, u_2, u_3, u_4$を与えてあげれば、ユニットの出力$z_1, z_2, z_3, z_4$は以下のようになります。
z_1 = f(u_1)\\
z_2 = f(u_2)\\
z_3 = f(u_3)\\
z_4 = f(u_4)
これを行列表現すれば、かなり見通しがいいですね。
\left[
\begin{array}{rrr}
u_1 \\
u_2 \\
u_3 \\
u_4
\end{array}
\right]
=
\left[
\begin{array}{rrr}
w_{11} & w_{12} & w_{13} & w_{14}\\
w_{21} & w_{22} & w_{23} & w_{24}\\
w_{31} & w_{32} & w_{33} & w_{34}\\
w_{41} & w_{42} & w_{43} & w_{44}
\end{array}
\right]
\left[
\begin{array}{rrr}
x_1 \\
x_2 \\
x_3 \\
x_4
\end{array}
\right]
+
\left[
\begin{array}{rrr}
b_1 \\
b_2 \\
b_3 \\
b_4
\end{array}
\right]
⇒
{\bf u} = {\bf w} {\bf x} + {\bf b}
\left[
\begin{array}{rrr}
z_1 \\
z_2 \\
z_3 \\
z_4
\end{array}
\right]
=
f\left(
\left[
\begin{array}{rrr}
u_1 \\
u_2 \\
u_3 \\
u_4
\end{array}
\right]
\right)
⇒
{\bf z} = f({\bf u})
1.3 多層ネットワーク
複数の層から出来ている順伝搬ネットワークを多層ネットワークといいます。
第1層の情報を${\bf z^{(1)}} = {\bf x}$、第2層の新しい情報を${\bf u^{(2)}}$、第1層から第2層への重みを${\bf w^{(1)}}$、第1層から第2層へのバイアスを${\bf b^{(1)}}$とすれば、
{\bf u^{(2)}} = {\bf w^{(1)}} {\bf z^{(1)}} + {\bf b^{(1)}}
と書けるので、第$l+1$層の新しい情報は、下のようの簡潔に表わすことができます。
{\bf u^{(l+1)}} = {\bf w^{(l)}} {\bf z^{(l)}} + {\bf b^{(l)}}
各層$(l = 1, 2, 3, \cdots)$に対して、適切な活性化関数$f^{(l)}$を用意してあげれば、各層のユニットの出力は以下のようになります。
{\bf z^{(l+1)}} = f^{(l+1)}({\bf u^{(l+1)}})
1.4 順伝搬型ネットワークの設計
1.2, 1.3の内容から以下のようなことがわかります。
入力から、重みとバイアスを用いて、出力が計算される
⇒ 入力から期待する結果を得るには、重みとバイアスを調節してあげればよい
従って、順伝搬型ネットワークの設計のアプローチとしては以下のようになります。
- 入力に対する期待する結果を用意する
- 重みとバイアスを調節して、入力から期待する結果得るようにする
ここで、入力を${\bf x}$、出力を${\bf y}$としたときの、順伝搬型ネットワークを${\bf y} = F({\bf x; w, b})$として定義することにします。
1.4.1 学習の枠組み
まず入力に対する期待する結果を用意します。
例えば、手書きの数字を認識させるとき、手書きの数字と期待する数字をペアでデータとして、いっぱい持っておきます。
この1つ1つのデータを訓練サンプルといい、その集合を訓練データと呼びます。
ここでは、1つの入力を$x$、その期待する出力を$y$と定義します。
すると、N個の訓練サンプルは$d_1 = (x_1, y_1), d_2 = (x_2, y_2), \cdots, d_N = (x_N, y_N)$と定義でき、
訓練データは{$(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)$}と表現できます。
次に、重みとバイアスを調節して訓練データ通りの結果にしたいけど、どうやって調節していくのか。
それは、ネットワークが表す関数$F$と訓練データとの近さを表す尺度を決めて、できるだけ差が少なくなるようにパラメータを調節します。
その尺度を表す関数を損失関数と呼びます。
どうも、考える問題について、適切な活性化関数と損失関数の組み合わせがあるようです。
先人の知恵をお借りすると、考える問題別に以下の組み合わせが一般的のようです
| 問題の種別 | 活性化関数 | 損失関数 |
|---|---|---|
| 回帰 | 恒等写像 | 二乗誤差 |
| 二値分類 | ロジスティック関数 | エントロピー誤差 |
| 多クラス分類 | ソフトマックス関数 | 交差エントロピー誤差 |
回帰とは、出力値に連続値をとる関数を対象に訓練データをよく再現するような関数を定める問題のこと。
例えば、「身長から体重を推測する」とか「「広告宣伝費」と「来店者数」の関係から推測する」など。
二値分類は、入力の内容に応じて、2種類に区別する問題のこと
例えば、「顔の写真を与えた時に性別を判断する」など。
多クラス分類は、入力の内容に応じて、有限個のクラスに分類すること
例えば、「手書きの数字を入力して、数字を判断する」など。
なので、顔の写真を与えて、「~しているとき」「~していないとき」の判定を行なうときは二値分類のアプローチ、
「笑顔」「怒っている顔」「寝ている顔」「びっくりした顔」など判定したいときは多クラス分類のアプローチとなります。
あとは、式だけ紹介します。
恒等写像
f(u) = u
ロジスティック関数
f(u) = \frac{1}{1+e^{-u}}
ソフトマックス関数
f_{k}^{(l)}(u) = \frac{\exp( {u_k^{(l)}} )}{\sum_{j=1}^{K} \exp( {u_j^{(l)}} )} (Kは各層のユニット数)
二乗誤差
E({\bf w, b}) = \sum_{n=1}^{N} || d_n - F({\bf x_n; w, b}) ||
エントロピー誤差
E({\bf w, b}) = -\sum_{n=1}^{N} [d_n \log(F({\bf x_n; w, b})) + (1 - d_n) \log(1 - F({\bf x_n; w, b}))]
交差エントロピー誤差
E({\bf w, b}) = -\sum_{n=1}^{N} \sum_{k=1}^{K}[d_{nk} \log(f_{k}^{(L-1)}({\bf x_n; w, b})))]
次回は、確率的勾配降下法で、重みとバイアスの調節を行なう方法について書きます。