11 Dec 2024: しばらくぶりに見たらもともとのウェブサイトのドメインが他者に取得されていたので,リンクを除去ないし github に更新しました.最近は webassembly がアツいんですかね.
追記 (9 Aug 2015) : haste 5.0 がリリースされました(メーリングリストへの投稿).Major release ということでいくつか破壊的な変更が含まれており(とはいっても,ざっと眺めた感じ移行は比較的しやすそうです),Haste 0.4.4 で書かれたこのコードはそのままでは 0.5ではコンパイルが通りません.#コードをちょっと眺める の節を読むときには outdated なコードであることにご留意ください.
追記2 (19 Aug 2015) : 少し遅くなりましたが Haste 0.5.0 に合わせてアップデートしました.計測していませんがパフォーマンスが(Haste のバージョンアップによって)良くなっている可能性があります. コードの差分はこちらです.今回書いたコードでは Event まわりの取り扱いが微妙に変わったのみです.以下の記事は更新していませんので差分をちょっと眺めてから読んでください.
しばらくまえに Fourier 級数のかっこいい可視化が流れてきていたので,Haskell と Haskell -> javascript のコンパイラである Haste を使ってブラウザ上で見られるようにしてみた,という話.書いたのはしばらく前で,ひとりで満足していたのですが,Haste の布教を兼ねて紹介してみます.
僕自身は情報系の人間ではないし,パッと書いてあまり推敲していないので,そんなに綺麗なコードにはなっていないと思いますし,あるいは「それはアカン」みたいなこともやっているかもしれません.
とりあえずいい感じに動くものができたので,"Haskell + haste でこんなことも割と簡単にできちゃうよ!" みたいなのが主題です(もちろん,何かしらの指摘をいただけるのでしたらそれはすごく嬉しいですが).
成果物
どうぞ.動いてる部分自体は haskell およそ 100行です.無限に眺めていられる.
Haste とは
Haste on github はHaskell から javascript へのコンパイラの1つで,ほとんどのGHC拡張 (template haskell は残念ながらまだらしい)を含めた haskell 全体をサポートしており,要するに javascript で扱いたいもろもろのことを可能にするHaste.なんちゃら達を import すればあとは普通の haskell でかけます.
- 普段お使いの haskell 環境でそのまま使える (
ghc-modも通るし neco-ghc などの補完もききます) - Type-safe!
- javascript との連携も容易
- かなり速い模様.
- etc.
Haste 自身については本題ではないので細かくは省きます.少なくとも趣味で使うぶんにはすごくいいのでお勧めです.
ドキュメントがほしい〜と言う場合には,レポジトリについてる example を眺めると共に,API Docs を見るといいかんじです(このあたりは haskell の楽さですね).とりあえず 気軽にお絵かきをするなら Haste, Haste.DOM, Haste.Graphics.Canvas あたりを見ると良さそう.
やっていること
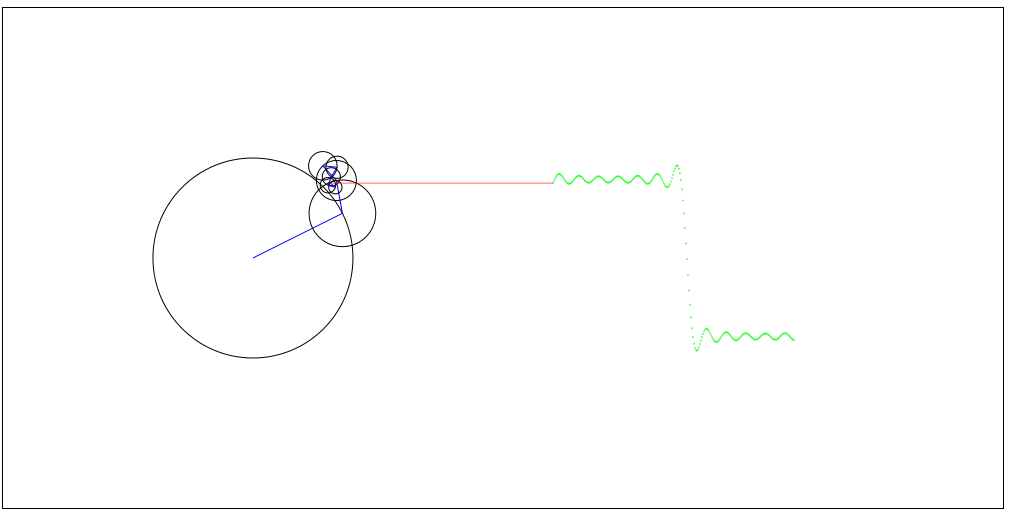
可視化のアイデアは要するに,$\sum a_k \sin (kx)$ を半径 $a_k$ の円の集まりで表現しようというものです.
半径$a_1$ の円を描き,偏角 $x$ のところに点を打って,そこを中心に半径$a_2$の円を書いて,偏角$2x$に点を打って,…と繰り返せば最終的に行き着く点(のy座標)が求めるものになります.各 $a_k$ は不変,$x$ を時間に応じて変化させればつまるところ円がかみあいながら動いていくようないい感じのものができる. 右に線を伸ばして見やすくし,過去の値をオシロスコープふうに見せてやればかっこ良い,といった具合ですね.
sin 側だけを問題にしているので,大雑把に言えば"次の点" を $(\cos x, \sin x)$ に打つか,$(-\cos x, \sin x)$ に打つかは任意です.今回は矩形波とかでそれっぽくなるように適当にやってもらいました.
コードをちょっと眺める
今回書いたソース は 3 ファイルにわかれています.
- Consts.hs : 1コマで偏角をどのくらい変えるとか,基本の円の大きさとかそういう値
- Fouriers.hs : いろんな Fourier 級数の定義.Haste は遅延評価も扱えるので,それぞれ無限リストとして定義しています.
- Fouricle.hs : これがメイン.
Fouricle.main
main = do
θref <- newIORef 1
fsRef <- newIORef []
dθref <- newIORef defaultdθ
setUp fsRef dθref
Just canv0 <- getCanvasById "canv0"
Just canv1 <- getCanvasById "canv1"
mainLoop canv0 canv1 dθref fsRef θref
あまり頭を使わず,3つの IORef を使っています.θ : 現在の角度,fs : 現在描いているフーリエ級数,dθ : 現在の1コマあたりの θ の増分.後ろ2つはあとから,ブラウザから設定できるように追加したもので,変更時にやることを考えるのが面倒だったのでもう全部 IORef でいいやってなったんですが,パフォーマンスは大丈夫そうです.
getCanvasById は ID から Canvas を得る函数で,型は MonadIO m => ElemID -> m (Maybe Canvas) です(type ElemID = String).
setUp を見てみましょう.ここでは級数と速さの倍率がブラウザから変更された場合に上の値を書き換えることを定義しています(随分手続き的だなぁという気もします).
setUp :: IORef Fourier -> IORef Angle -> IO ()
setUp fsRef dθref = do
Just series <- elemById "series"
Just nth <- elemById "nth"
setFs fsRef
_ <- onEvent series OnChange (setFs fsRef)
_ <- onEvent nth OnChange (setFs fsRef)
Just speed <- elemById "speed"
_ <- onEvent speed OnChange $ do
newdθ <- (*defaultdθ) . read <$> getProp speed "value"
writeIORef dθref newdθ
return ()
elemById は大体において document.getElementById です.series, nth にはそれぞれ「どの級数の」「何項目まで」使うかが入っていて,これの onChange で値の更新を頼んでいます.
お待ちかね mainLoop
mainLoop :: Canvas -> Canvas -> IORef Angle -> IORef Fourier ->
IORef Angle -> IO ()
mainLoop c0 c1 dθref fsRef θref = do
fs <- readIORef fsRef
θ <- readIORef θref
drawCurrent c0 c1 fs θ
dθ <- readIORef dθref
let θ' = θ + dθ
nextθ = if θ' > 2*pi then θ' - 2*pi else θ'
writeIORef θref nextθ
setTimeout stepTime (mainLoop c0 c1 dθref fsRef θref)
繰り返しますとここで IORef が登場しているのは専らブラウザ側からの更新に対応する一番頭を使わない対応であるからです(あと IORef にちょっと親しみ始めた頃なので使ってみたかったというのもある).setTimeout なんてありがたい函数があるのでこれを使ってループします.
Canvas を二枚使っているのにお気づきでしょう.これは,円がぐるぐる回ってる方は各コマで過去の描画を捨てたいのに対し,右にでるグラフは過去の履歴を保存したいので,Canvas を二枚重ねて一方に(各コマで clear しながら)円を,もう一方に(各コマで右に少しずつずらしながら)グラフを描画していることによります.もうひと手間かけて,裏で描画したのを一枚の canvas に併せて表示すればよかったんですけど,まあいいかと思ってしまった.
drawCurrent が実際に描画を行う函数です.
drawCurrent :: Canvas -> Canvas -> Fourier -> Angle -> IO ()
drawCurrent c0 c1 fs θ = do
-- draw c0
p <- newIORef ((0,0) :: Point)
refresh c0
forM_ (zip [1..] (map (*radius) fs)) $ \ (n,a) -> do
(nx,ny) <- readIORef p
let dx = if (floor (n+0.4) `mod` 4) > 1
then -a * cos (n*θ)
else a * cos (n*θ)
dy = a * sin (n*θ)
renderOnTop c0 . toCenter . stroke $ circle (nx,ny) (abs a)
renderOnTop c0 . toCenter . color blue . stroke $ line (nx,ny) (nx+dx,ny+dy)
modifyIORef' p (\(x,y) -> (x+dx, y+dy))
(x,y) <- readIORef p
renderOnTop c0 . toCenter . color red . stroke $
line (x,y) (fromIntegral $ barLength-width `div` 2,y)
-- c1
shiftPrevious c1 (fromIntegral dw)
renderOnTop c1 . toOrigin . color green . fill $ circle (0,y) pointSize
Canvas 二枚,級数,今の角度を受け取って描画を行います.c0 のほうが円がぐるぐる動いてる方.
c0 の描画から見てみましょう.まず原点からはじめ,canvas を綺麗にします(js なら .width+=0; みたいなことすればできる処理で,こっちでどうすると一番いいのかわからない).順番に円を描いては (x,y) を更新して,というような愚直なことをしています.最後に終わったところから横にびびっと線を引きます.
Haste での描画のメカニズムはこういう感じ:
-
circleとかがShapeをつくる -
strokeなどで それをPictureに -
color redとかはPicture->Picture. -
renderやrenderOnTopでPictureをCanvasに描画する.
続いて グラフのほうの描画をしたい.i) 現在のグラフを右にちょっとずらしてコピー, ii) 今居る点を追加 でいける…のですが,Haste の枠内で,Canvas の画像をコピーして(右に)ずらして貼り付ける,というような処理のやリかたを見つけられませんでした(それっぽいのをみつけたのだけど失敗したので,やり直せば行ける気はする).仕方がないので ffi で javascript を呼んでいます.
shiftPrevious :: Canvas -> Double -> IO ()
-- TODO : nicer implementation
shiftPrevious = ffi . toJSString . unwords $
[
"(function(c,dx){",
"var buf = document.createElement('canvas');",
"buf.width = c.width; buf.height=c.height;",
"buf.getContext('2d').drawImage(c,0,0);",
"c.width = c.width;",
"c.getContext('2d').drawImage(buf,dx,0);",
"})"
]
気をつけるべきはこの函数が Canvas -> Double -> IO () なので,呼ぶべき javascript もそういう函数として定義するということです.見えないキャンバスを作り,今の瞬間のグラフをコピーして,少しずらして元のに貼り付ける.怪我の功名というか,おかげで javascript 呼ぶのもすごく簡単なのがわかりますね.
まとめ
- Haste すごくいい
- 気楽に使えるのでみんな使ってほしい
蛇足
Haskell (に限らずですが)の1つの難点はちょっとした成果物をコードを書かない知り合いあるいは知り合いでないひとに見せびらかしにくいことだと思います.Haste を使えばぱっとちょっと派手なものを作って遊べますし,またHaskell を書いているうちに(慣れ的に,あるいは心情的に)javascript を書けなくなったというひとにも救済となります.
Haskell の気持ちよさで javascript を生成できるの,思った以上に楽ですよ.ぜひお試しください.
ちなみに.非ASCIIな文字をコードに使うの否定派だったのですが,θ とかは思った以上に便利.視覚的に「あ,角度だな」と常に訴えかけてくれるのでよいです.Vim なら <C-k>h* とタイプも楽ですしね.
PS: 何かどっかでスタックが積みあがったりしないかなーと思って一時間位放置しておいたのですがその範囲では特にメモリ使用量とかは増えてなさそうです.