kuromoji.js使って構文解析した

こんにちは、らこです。先日から話題になってるJavaScriptの形態素解析器kuromoji.jsを使って、確率自由文脈文法で構文解析してみました。(注意:アルゴリズムの解説記事 ではない です)

結論

kuromoji.js遊びまくれるのでみんな使おう

kuromoji.d.ts書いた

私は型大好き人間なのでTypeScript使ってkuromoji.js使いました。型定義ファイルは自分が使う部分だけエイヤっと自作しました(laco0416/kuromoji.d.ts)。

あと、プロジェクトに↑の自作型定義ファイルを読み込むのにdtsm使いました。tsd使ってたのが馬鹿らしくなるくらい便利です。作者のvvakameさんによるわかりやすい紹介はこちら

確率自由文脈文法とは

ちゃんと説明すると長くなりますしうまく説明できる自信もないので、ばっさりカットします。

雰囲気つかむにはここらへんを読んでいただければいいかと思います。

Wikipedia 確率文脈自由文法

統計的手法による 文法モデリングと構文解析

4.構文解析 - Google スライド

ちゃんと知ろうと思うなら

Amazon.co.jp： 言語と計算 (4) 確率的言語モデル: 北 研二, 辻井 潤一: 本

は必読です。

アルゴリズムの実装

確率自由文脈文法によって構文木を作るには内側外側アルゴリズムを用いた。TypeScriptでの実装例がこちら。クラスの構造とかいろいろ省いてますが内側外側アルゴリズムの部分だけ抜粋しました。一応ソースコードはこちら

  calc(tokens:Token[]):boolean {
    var N = tokens.length;
    this.nodeMap = new Array(N).map((v)=>new Array(N));
    this.ruleTreeMap = new Array(N).map((v)=>new Array(N));
    //内側初期化
    for (var i = 0; i < N; i++) {
      this.nodeMap[i] = [];
      this.ruleTreeMap[i] = [];
      var pos = Pcfg.getJoinedPos(tokens[i]);
      this.nodeMap[i][i] = new PcfgNode();
      this.nodeMap[i][i].inside[pos] = 1.0;
      this.ruleTreeMap[i][i] = new RuleTree.Node();
      this.ruleTreeMap[i][i].rules[pos] = [Rule.endRule(pos)];
    }
    //ボトムアップ
    for (var n = 1; n < 1 + N - 1; n++) {
      for (var i = 0; i < N - n; i++) {
        var x = i;
        var y = i + n;
        for (var j = 1; j < 1 + n; j++) {
          for (var ruleIndex = 0; ruleIndex < this.rules.length; ruleIndex++) {
            var rule:Rule = this.rules[ruleIndex];
            //CYK
            var left = this.nodeMap[x][x + (j - 1)].inside[rule.result1];
            if (!left) {
              left = 0;
            }
            var bottom = this.nodeMap[x + j][y].inside[rule.result2];
            if (!bottom) {
              bottom = 0;
            }
            if (!this.nodeMap[x][y]) {
              this.nodeMap[x][y] = new PcfgNode();
            }
            var old = this.nodeMap[x][y].inside[rule.source];
            if (!old) {
              old = 0;
            }
            this.nodeMap[x][y].inside[rule.source] = old + rule.probability * left * bottom;

            if (rule.probability * left * bottom > 0) {
              //最尤推定用
              if (!this.ruleTreeMap[x][y]) {
                this.ruleTreeMap[x][y] = new RuleTree.Node();
              }
              if (!this.ruleTreeMap[x][y].rules[rule.source]) {
                this.ruleTreeMap[x][y].rules[rule.source] = <Rule[]>[rule];
              }
              else {
                this.ruleTreeMap[x][y].rules[rule.source].push(rule);
              }
              this.ruleTreeMap[x][y].left[rule.toString()] = {x: x, y: x + (j - 1)};
              this.ruleTreeMap[x][y].right[rule.toString()] = {x: x + j, y: y};
            }
          }
        }
      }
    }
    //非受理判定
    if (!this.nodeMap[0][N - 1] || this.nodeMap[0][N - 1].inside["S"] == 0) {
      return false;
    }
    //外側初期化
    for (var i = 0; i < N; i++) {
      for (var n = 0; n < N - i; n++) {
        for (var source in Pcfg.toUniqueArray(this.rules.map((x) => x.source))) {
          if (this.nodeMap[i][i + n].inside[source] == 0) {
            this.nodeMap[i][i + n].outside[source] = 0;
          }
        }
      }
    }
    //頂点定義
    this.nodeMap[0][N - 1].outside["S"] = 1;
    //トップダウン
    for (var n = N - 1; n >= 0; n--) {
      for (var i = 0; i < N - n; i++) {
        var x = i;
        var y = i + n;
        for (var ruleIndex = 0; ruleIndex < this.rules.length; ruleIndex++) {
          var rule = this.rules[ruleIndex];
          if (this.nodeMap[x][y].outside[rule.source] > 0) {
            for (var k = 1; k < 1 + n; k++) {
              //下側
              if (this.nodeMap[x + k][y].inside[rule.result2] > 0) {
                this.nodeMap[x + k][y].outside[rule.result2] =
                  this.nodeMap[x + k][y].inside[rule.result2] +
                  (rule.probability *
                  this.nodeMap[x][y].outside[rule.source] *
                  this.nodeMap[x][x - (1 - k)].inside[rule.result1]);
              }
              //左側
              if (this.nodeMap[x][y - k].inside[rule.result1] > 0) {
                this.nodeMap[x][y - k].outside[rule.result1] =
                  this.nodeMap[x][y - k].outside[rule.result1] +
                  (rule.probability *
                  this.nodeMap[x][y].outside[rule.source] *
                  this.nodeMap[y + (1 - k)][y].inside[rule.result2]);
              }
            }
          }
        }
      }
    }
    return true;
  }

長いので一つ一つは説明しませんが、内側確率の計算は完全にCYK法です。自分で考えたわけではなくて「確率的言語モデル」読みながら書きました。

構文木の頂点にはSが記号があって、ものすごく乱暴に言うと内側確率では末端からSを導く確率を、外側確率ではSから末端を導く確率を求めてます。

できたもの

このアルゴリズムを使って構文木作りました

index.ts

import kuromoji = require("kuromoji");
import Token = kuromoji.Token;
import Pcfg = require("./pcfg");
import Rule = require("./rule");
import RuleTree = require("./rule_tree_node");

var rules:Rule[] = [
  "S>名詞句 形容詞 0.5",
  "S>名詞句 名詞 0.3",
  "S>名詞句 動詞 0.2",
  "名詞>形容詞 名詞 1",
  "名詞句>名詞 助詞 1",
  "形容詞>名詞 助詞 0.1",
  "形容詞>名詞 動詞 0.2",
  "形容詞>副詞 形容詞 0.4",
  "形容詞>副詞 形容詞 0.3",
  "動詞>副詞 動詞句 0.5",
  "動詞>名詞 助動詞 0.5"
].map((expr)=>Rule.fromString(expr));

var text = "隣の客はよく柿食う客だ";
console.log("text=" + text);
rules.forEach((v)=>console.log(v.toString(), v.probability));
Pcfg.parse(text, rules, (nodeTree, tokens, newRules)=> {
  console.log("### result ###");
  if (!nodeTree) {
    console.log("Cannot parse");
  }
  else {
    var N = nodeTree.length;
    display(nodeTree, tokens, 0, N - 1, "S");
    newRules.forEach((v)=>console.log(v.toString(), v.probability));
  }
});

function display(tree:RuleTree.Node[][], tokens:Token[], x:number, y:number, pos:string, depth = 0, leafCount = 0) {
  var top = tree[x][y];
  if (top === undefined) return leafCount;
  var result = "";
  var rule:Rule = top.rules[pos].sort((a, b)=> a.probability < b.probability ? -1 : 1)[0];
  if (rule.result1 == "END") {
    result = "--->" + tokens[leafCount].surface_form;
    leafCount++;
  }
  else {
    result = "(" + rule.probability.toString() + ")";
  }

  console.log(new Array(depth * 4).join(" "), rule.source, result);
  if (rule.result1 !== "END") {
    leafCount = display(tree, tokens, top.left[rule.toString()].x, top.left[rule.toString()].y, rule.result1, depth + 1, leafCount);
  }
  if (rule.result2 !== "END") {
    leafCount = display(tree, tokens, top.right[rule.toString()].x, top.right[rule.toString()].y, rule.result2, depth + 1, leafCount);
  }
  return leafCount;
}

結果はこちら

stdout

text=隣の客はよく柿食う客だ
S>名詞句 形容詞 0.5
S>名詞句 名詞 0.3
S>名詞句 動詞 0.2
名詞>形容詞 名詞 1
名詞句>名詞 助詞 1
形容詞>名詞 助詞 0.1
形容詞>名詞 動詞 0.2
形容詞>副詞 形容詞 0.4
形容詞>副詞 形容詞 0.3
動詞>副詞 動詞句 0.5
動詞>名詞 助動詞 0.5
### result ###
 S (0.5999999999999994)
    名詞句 (1)
        名詞 (1)
            形容詞 (0.175)
                名詞 --->隣
                助詞 --->の
            名詞 --->客
        助詞 --->は
    動詞 (0.7499999999999999)
        名詞 (1)
            形容詞 (0.275)
                副詞 --->よく
                形容詞 (0.225)
                    名詞 --->柿
                    動詞 --->食う
            名詞 --->客
        助動詞 --->だ
S>名詞句 形容詞 0.2500000000000003
S>名詞句 名詞 0.15000000000000024
S>名詞句 動詞 0.5999999999999994
名詞>形容詞 名詞 1
名詞句>名詞 助詞 1
形容詞>名詞 助詞 0.175
形容詞>名詞 動詞 0.225
形容詞>副詞 形容詞 0.325
形容詞>副詞 形容詞 0.275
動詞>副詞 動詞句 0.2500000000000001
動詞>名詞 助動詞 0.7499999999999999

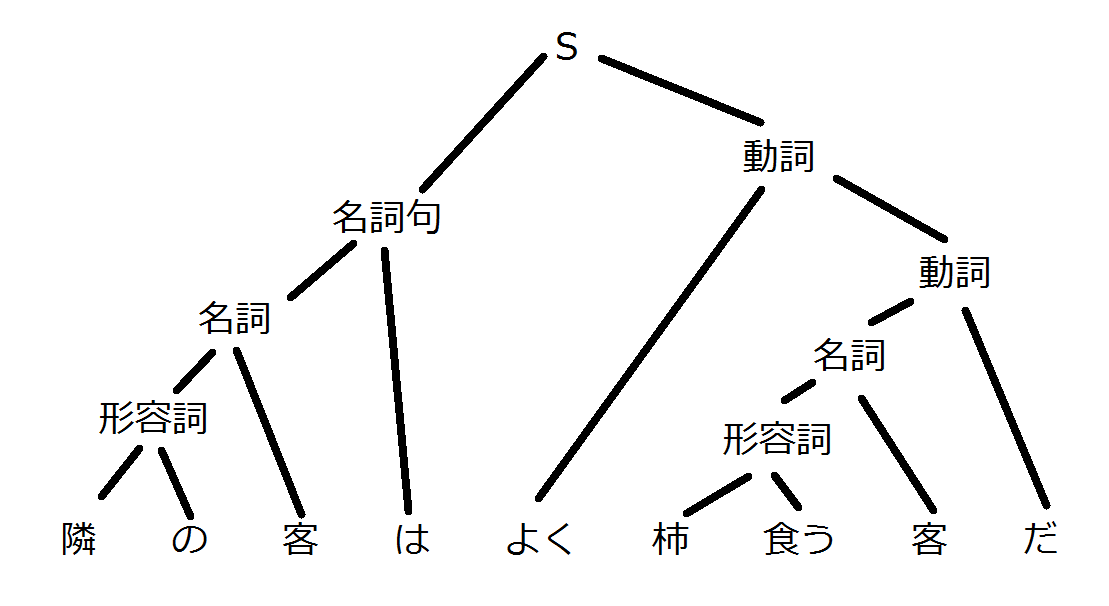
図解するとこう

最初と最後で規則の確率が変わっていますが、これはこの構文木を作るのに使われた回数によってそれぞれの規則の確率を補正してるからです。EMアルゴリズムってやつです。本来ならこれの規則の集合をどっかにストアして、また別のデータを食わせて補正かけていくことで、自分だけの構文解析器を育てていきます。

何がいいたいのか

kuromoji.js本当にすごい。このコード、実は以前にC#でほとんど同じものを実装していて、その時はmecabを呼び出して使ってたんですが、体感ではその時とスループットほとんど変わりません。JavaScriptすごいって感じです。

形態素解析が出来れば、そのデータの使い道は無限にあります。kuromoji.jsは読みも出力できるので音声認識や音声合成にも使えそうですし、kuromoji.jsでみんなカジュアルに自然言語処理を始めましょう。