暗号化された通信内の実際のプロトコルを、ニューラルネットワークで識別してみる

はじめに

暗号化された通信内の実際のプロトコルは、暗号を解かないとわからない、と通常は考えられています。暗号化した後のトラヒックの特徴からニューラルネットワークで、プロトコルが識別できるか試してみました。結果としては95%以上の精度で識別できました。先週試してみた暗号化通信かどうかの二値分類識別の発展版です。
http://qiita.com/kznx/items/96f670b7a4b3a94d5aaa

試してみた条件

ニューラルネットワーク：全結合の隠れ層5層
入力：1フローあたり22個の統計量
出力：13プロトコル識別
フレームワーク：keras (tensorflow backend)
データセット：NIMS Data set を一部変更して利用
https://projects.cs.dal.ca/projectx/Download.html

コードとデータセット

githubに置きました。
https://github.com/kznx/traffic_classification/tree/master/ssh_classification

前準備

データセットの読み込み、正規化、データの分離、正解データのフォーマットを変更、あたりは、下記の投稿と同じです。
http://qiita.com/kznx/items/96f670b7a4b3a94d5aaa

ちなみにオリジナルのNIMSデータセットは、プロトコルごとのフロー数に大きく偏りがあったので、各プロトコル同じフロー数 (2000) になるよう、オリジナルのデータセットからランダムに抽出しています。

モデル定義、学習、評価

仮で隠れ層を5層にしてみました。

# モデルの定義
model = Sequential()

# ネットワークの定義
model.add(Dense(input_dim=22, output_dim=40))
model.add(Activation('relu'))
model.add(Dropout(0.2))

model.add(Dense(input_dim=40, output_dim=30))
model.add(Activation('relu'))
model.add(Dropout(0.2))

model.add(Dense(input_dim=30, output_dim=30))
model.add(Activation('relu'))

model.add(Dense(input_dim=30, output_dim=20))
model.add(Activation('relu'))
model.add(Dropout(0.2))

model.add(Dense(input_dim=20, output_dim=10))
model.add(Activation('relu'))

model.add(Dense(input_dim=10, output_dim=20))
model.add(Activation('relu'))

## OUTPUT  SSH or NOTSSH
model.add(Dense(output_dim=13))
model.add(Activation('softmax'))

rms = RMSprop()
# ネットワークのコンパイル
model.compile(loss = 'categorical_crossentropy',
##              optimizer = 'sgd',
              optimizer = rms,
              metrics = ['accuracy'])

## コールバック
## es_cb = EarlyStopping(monitor='val_loss', patience=10, verbose=1, mode='auto')
tb_cb = TensorBoard(log_dir='./logs', histogram_freq=0, write_graph=True, write_images=True)

# 学習処理
hist = model.fit(train_x, y_train, nb_epoch = 1000, batch_size = 200, verbose=1, 
                callbacks=[tb_cb])

# 学習結果の評価
score = model.evaluate(test_x, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

結果

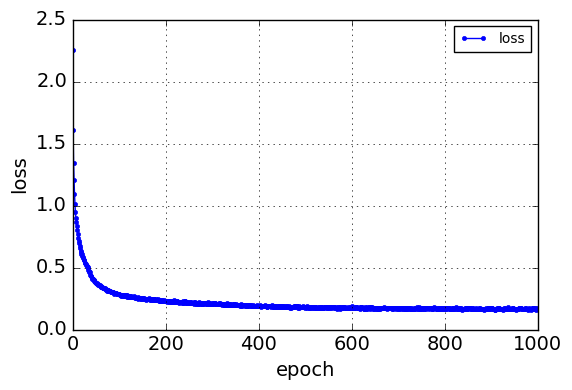
収束には少なくとも、500 Epochぐらい必要でした。

最終的には95%以上の精度を達成できました。暗号化してても中身のプロトコルはだいたい推測できてしまうのは、ちょっと意外な感じでした。せいぜい80%ぐらいかと。

Epoch 1/1000
19200/19200 [==============================] - 0s - loss: 2.2545 - acc: 0.1989     
Epoch 2/1000
19200/19200 [==============================] - 0s - loss: 1.6081 - acc: 0.3345     
Epoch 3/1000
19200/19200 [==============================] - 0s - loss: 1.3452 - acc: 0.4067   
...
Epoch 997/1000
19200/19200 [==============================] - 0s - loss: 0.1611 - acc: 0.9513     
Epoch 998/1000
19200/19200 [==============================] - 0s - loss: 0.1617 - acc: 0.9515     
Epoch 999/1000
19200/19200 [==============================] - 0s - loss: 0.1614 - acc: 0.9507     
Epoch 1000/1000
19200/19200 [==============================] - 0s - loss: 0.1755 - acc: 0.9503     
4736/4800 [============================>.] - ETA: 0sTest loss: 0.118659284911
Test accuracy: 0.965208333333

ちなみに、学習時間は、1000 Epochで、4年ほど前の MacBook Pro、CPUのみで 10分程度で完了します。

この後は、もう少し簡単なニューラルネットワークにできるのかどうか、試して見るつもりです。