今回のお題
インスパイアされた元記事ではおみくじではなくガチャなんですが、、、
確率が明らかになったところで,それを正しく理解できなければ意味がない。よくある間違いが,「出現確率1%なら,100回ガチャを引けばほぼ確実に出るだろう」という思い込みだ。実際のところ,ガチャを100回引いて出現確率1%のものが当たる確率は約63%でしかない。表現を変えれば,100人のプレイヤーがそれぞれ100回引くと,63人は当たるが,残り37人は100回全部ハズレ,という感じだ。
http://www.4gamer.net/games/999/G999905/20160305003/
実際にはどういうことなんでしょうか?
数学的な背景、Pythonで計算&図示までを簡単にご紹介。
確率論的には
1回あたり1%の確率で当たりが出るガチャを連続100回引いた場合、1回も当たりが出ないことがある?!
ということですね。神社にあるおみくじだと1回引いたおみくじは通常元に戻しません(その代わり、神社の境内のどっかに結んだりしますねー)ので、1回引くごとに全おみくじから1枚ずつ減っていきます(非復元抽出)。
今回のガチャでは、常に100枚のくじのうち1回が当たり、、という状況なので、復元抽出に当たりますね。(おみくじで言えば自分のくじを元に戻すことに相当)
Pythonで計算してみよう
ということで、
1回あたり1%の確率で当たりが出るガチャを連続100回引いた場合、1回も当たりが出ないことがある?!
を定量化してみます。これは、要は100回連続でハズレを引き続けることに相当するので
(1-0.01)^{100}=0.99^{100}
を計算させればいいですね。pythonで計算させると、
>>> 0.99**100
0.3660323412732292
なので0.366≒36.6%程度1回も当たらないことになりますね(残念)。これは、元記事の
残り37人は100回全部ハズレ,という感じだ。
の部分ですね。
数学的にちゃんと考える
今回の場合、非復元抽出で100回連続試行しますので、数学では「二項分布」が相当します。
よくある話が「コインの裏、もしくは表が100回中何回出るか?」みたいな文脈ですが、オモテウラの出方がイビツで「表が出る確率が0.01、裏が出る確率が0.99」のような状況です。(どんなコインか見てみたいものですが、、)
定式化
そうすると、100回の非復元抽出でr回当たりが出る確率は
\begin{eqnarray}
{}_{100} C _r\times 0.01^r\times (1-0.01)^{100-r}
\end{eqnarray}
幾つか計算してみる
r=1のとき
\begin{eqnarray}
{}_{100} C_1\times 0.01\times (1-0.01)^{99} = 100\times 0.01\times 0.99^{99}=0.3697...
\end{eqnarray}
⇒大体0.370くらいなんで、1回も当たりを引かない確率と、1回当たりを引く確率が大体一緒なんですね。
r=2のとき
\begin{eqnarray}
{}_{100} C_2\times 0.01^2\times (1-0.01)^{98} = 4950\times 0.01^2\times 0.99^{98}=0.1849...
\end{eqnarray}
⇒今度は0.18くらいなので、いきなり確率が半減してしまいます、、、
確率分布描いてみっか
、、、と個々のケースを都度都度考えているのも大変なので、(確率)分布を描いてみると全体像が見えてきそうです。
Pythonでグラフを描いてみる
import pandas as pd
import numpy as np
init = 0
trial = 100
prob = 0.01
### 組み合わせを再帰的に計算
def comb(n, r):
if n == 0 or r == 0: return 1
return comb(n, r-1) * (n-r+1) / r
### r回当たりである確率を計算
def binominal(n,r,p):
return comb(n,r)*(p**r)*((1-p)**(n-r))
### 関数のベクトル化
bi = np.vectorize(binominal)
### 試行回数を配列で持たせる
arr = np.arange(init, trial)
### 二項分布をベクトル演算で計算
plot_values = pd.DataFrame(bi(trial, arr, prob), columns=['probability'])
### 図示
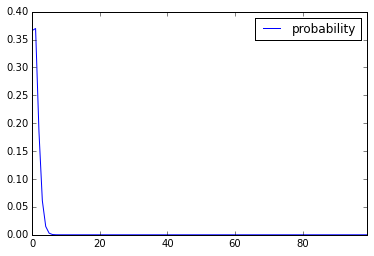
plot_values.plot()
⇒0や1の付近でピークが終わり、急激に確率が0に近づいていますね、、、(汗)
Poisson分布
↑の分布、どっかで見たなー、という方は鋭いです。Poisson分布ですね。Wikipediaの「二項分布」のページでは
n が大きく p が十分小さい場合、np は適度な大きさとなるため、パラメータ λ = np であるポアソン分布が 二項分布B(n, p) の良好な近似を与える。すなわち、期待値λ = npを一定とし、nを十分大きくしたとき、
P[X=k]\simeq \frac{\lambda^ke^{-\lambda}}{k!}
とあります。我々はpythonを使ってr=0, 1, 2の計算を行いましたが、試しに上の式にk=0, 1, 2を当てはめてみましょうか。λ=100×0.01=1に注意すると一般に
P[X=k]\simeq \frac{1}{e\times k!}
なので、
P[X=0]=P[X=1]=\frac{1}{e} \simeq 0.3679...
となり、r=0, 1の時が確率が同程度であることが確認できますね。さらに、
P[X=2]=\frac{1}{2e}\simeq 0.1839...
なので、r=2の場合はr=0, 1の場合の確率の半分というところも大体合っていますね!