ランク学習のListNetをChainerで実装してみた #Python

はじめに

ランク学習 (Learning to Rank) の手法である、ListNetをChainerで実装します！

本記事は、Chainer Advent Calendar 2016 7日目です．

手法の説明

まず、ランク学習については、Advent Calender 5日目でsz_drさんが素晴らしい記事を書いているので、是非そちらをご覧ください。
時間のない方のために一言で言うと、「1セット（クエリ）の中に複数データがあり、それらに相対的な尺度が与えられたときに、教師付きの条件で順序付けを学習する」問題です。ラベルがクエリ間で絶対的な数値を取らないことが普通の教師付き学習との差になります。

RankNetとの違い

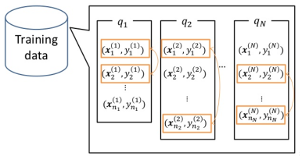
ニューラルネット+ランク学習で多くのの方が真っ先に思い浮かべるRankNetだと思います。実は、ランク学習の定式化方法は複数あり、RankNetはpairwise、ListNetはlistwiseな手法であるという差異があります。

Pairwise	Listwise

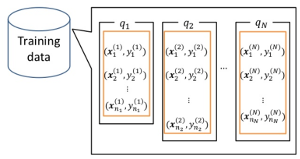1クエリからペアを無数にサンプリングして行う	1クエリごとに学習を行う

画像はDSIRNLP#1 ランキング学習ことはじめより引用

ListNetの基本的な考え方

ListNetはPermutation probability distribution (以下、PPD) という考え方に基づいています。PPDとは、下の図にあるように、データの各並び順 (permutation) の起こりやすさを確率分布にしたものです。PPDはデータごとのスコアから計算することができます。ある並び順Gが与えられたときに、その並び順PPDは次式で与えられます。

P(\pi|\mathbf{s}) = \prod_{j}^n{\frac{exp(s_j)}{\sum_{i=j}^{n}{exp(s_i)}}}

ただし、$s_j \in \mathbf{s}$はデータ$j$のスコア、$n$はクエリあたりのデータ数、$\pi$は並び順を示します。この式は$n=3$の例で書くと次式になります。

P(\pi) = \frac{exp(s_0)}{exp(s_0) + exp(s_1) + exp(s_2)}\frac{exp(s_1)}{exp(s_1) + exp(s_2)}\frac{exp(s_2)}{exp(s_2)}

Permutation Probability Loss （以下、PPL) は、2つのPPDのcross entropyをとって¹、

PPL = -\sum{P(\pi|\bar{\mathbf{s}}) \log P(\pi|\mathbf{s})}

PPLは、たとえば教師データに(1.0, 0.9, 0.8, ..)などと等間隔で数字をふって二乗損失で学習した場合に比べて、純粋に順序から学習できるという利点があります。

画像はYan Liu, Learning to Rank: from Pairwise Approach to Listwise Approachより引用。

ただし、すべての並び順の確率を計算すると、計算量が$L!$になってしまい、実用上計算できなくなってしまいます。そこで、一般にはトップ$k$個のならびだけを考慮することで$L!/(L-k)!$の計算量となる設定で行います²。

P(\pi|\mathbf{s}) = \prod_{j}^k{\frac{exp(s_j)}{\sum_{i=j}^{n}{exp(s_i)}}}

例えば、論文でも使ったとしている$k=1$の場合は、PPLはsoftmaxと同じ式になります。

ListNetはPPLを使うだけで、データごとのスコアの計算は任意の微分可能な関数で実装ができます。元の論文ではFeed forward NNで、スコア計算を実装しています。。

実装

まず、PPL ($k=1$) の実装です。


def permutation_probability_loss(x, t, length):
    length = length.reshape(-1, 1)
    # log_p: (batch size, n)
    log_p_x = x - F.broadcast_to(F.expand_dims(F.logsumexp(x, axis=1), 1), x.shape)
    # p_t: (batch size, n)
    p_t = F.softmax(t)

    # loss normalized over all instances
    loss = p_t * log_p_x
    mask = np.tile(np.arange(x.shape[1]).reshape(1, -1), (x.shape[0],  1)) < length
    mask = chainer.Variable(mask)
    padding = chainer.Variable(np.zeros(x.shape, dtype=x.dtype))
    loss = F.where(mask, loss, padding)

    return -F.sum(loss / length) / p_t.shape[0]

なお、今回はLが可変である前提で実装しました。lengthで不必要なデータをマスキングすることで、異なる長さのデータを同じバッチに流せるようになります。Pitfallとして、数式の計算を論文通りに行うと、割り算やexpの計算が不安定になるため、chainerにも用意されているlogsumexpを使う必要があります。

スコアの計算は(B, L, M)なる特徴量を受け取り、(B, L)なるスコアを出力するPerceptronで行いました。リスト内のデータはお互いに独立のため、(B, L, M)を(B, L * M)の形に修正し、最後に元に戻す形で実装しました。

class ListNet(chainer.Chain):
    def __init__(self, input_size, n_units, dropout):
        super(ListNet, self).__init__(
            l1=L.Linear(input_size, n_units),
            l2=L.Linear(n_units, 1))

        self.add_persistent("_dropout", dropout)

    def __call__(self, x, train=True):
        s = list(x.shape)
        n_tokens = np.prod(s[:-1])
        x = F.reshape(x, (n_tokens, -1))

        if self._dropout > 0.:
            x = F.dropout(x, self._dropout, train=train)
        o_1 = F.relu(self.l1(x))
        if self._dropout > 0.:
            o_1 = F.dropout(o_1, self._dropout, train=train)

        # o_2: (N*M, 1)
        o_2 = self.l2(o_1)

        return F.reshape(o_2, s[:-1])

すべての実装に関しては、githubに載せてあります。

実験

データセットはLETOR 4.0の、MQ2007を使用しました。時間がなかったので、パラメータはフィーリング決め打ちで、early stopping以外は特に工夫をしていません。

評価対象はmean average precision (MAP)です。

結果

TRAIN: 0.4693
DEV:   0.4767
TEST:  0.4877

(2017/8/29訂正: コメントを参照)

同じデータでの~~元論文~~著者らによる結果³。

TRAIN: 0.4526
DEV:   0.4790
TEST:  0.4884

うーん、随分差がついてしまっています。元の論文では「スコア計算にPerceptron」を使った、程度の粒度でしかかかれていないので、何か工夫があったのかもしれません。
大体同じ程度の性能が出ています。チューニングはあまりしないかわりに当時は存在しなかった手法を使うことでうまくいきました (i.e. Adam optimizer, dropout, ReLU activation)。(2017/8/29訂正)

ListNetの最大の利点はとにかく速いことでしょう。実際にベンチマークはしていないのですが、体感でRankNetの100倍程度速いと思います。

終わりに

今年はTensorflowとchainerを半々に使いましたが、試作スピード & デバッグはchainerが圧倒的に速いと思います。あと、cupyマジサイコー！
利用人数のせいか実装例が少なく、最近少々Tensorflowにおされ気味な気がするので、実装さらして盛り上げていきたいですね。

変更履歴：

2016/12/7: あまりにもざっくりとしていたので数式をたしました。
2017/8/27: ListNetのベンチマーク取得元を記載しました。
2017/8/29: 実験結果を更新しました。詳しくはコメントをご覧ください。また、レポジトリへのリンクを貼りました。
2017/12/22: 作者がベンチマークを再公開してくださったため、追記。

図には大きくKL divergence距離と書いてありますが、実際にはcross entropyを使っているようです。$P(\pi|\bar{\mathbf{s}})$が固定なので最適化としては結局同じになるためと思われます。 ↩
結局リストからサンプリングしてるじゃん！というつっこみはなしで。しかも、普通k=1で行う... ↩
https://www.microsoft.com/en-us/research/project/letor-learning-rank-information-retrieval/ にてベンチマーク結果が公開されていたと記憶していますが、 ~~2017/8/27時点で結果が非公開となっていました。~~ 作者にメールしたところ、再公開してくれました。 ↩