概要
12-10の問題は、
自民得票率と持ち家比率の相関係数を検定する問題です。
資料はかなり古い(1983年の総選挙!!)ですが、持ち家を持っているほど自民党が有利になるように見えて面白いです。
そこで、単に解くだけでなく、pandas, matplotlibあたりを使って、グラフも表示することにしました。
環境
- windows10 64bit
- python3.5
- jupyter-notebook
必要なライブラリなどは、http://www.lfd.uci.edu/~gohlke/pythonlibs/ からダウンロードしました。pip installで入れると動かないこともありました。
ライブラリ
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
データ作成
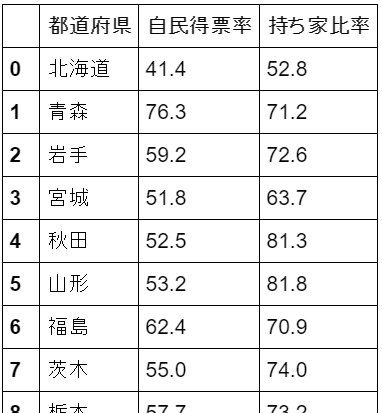
p.65 表3.13からコツコツとcsvにデータを入れこみます。
出来上がったcsvファイル(table_3_13.csvと名付けました。)を下記のようにして、dataframeに読みこみます
df = pd.read_csv('table_3_13.csv', encoding='shift-jis')
# 結果が文字化けするようであれば、encodeを確認します。
df
グラフ作成
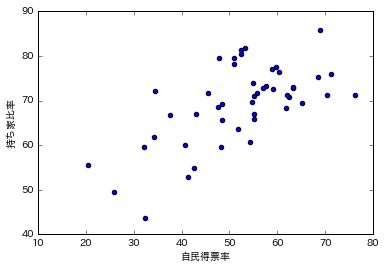
単純なグラフは下記のようにして表示します。
d = df[0:47] #北海道から沖縄だけの結果だけにしぼりました。
# グラフを見るとなんとなく相関があるように見える。
plt.xlabel(d.columns[1])
plt.ylabel(d.columns[2])
plt.scatter(d[[1]], d[[2]])
plt.show()
持ち家比率と自民党得票率には相関があるように見えます。
グラフの各要素に文字をつけて、どの県のものか分かるようにする。
# 各要素に文字をつける
fig, ax = plt.subplots(figsize=(15,15)) #グラフがある程度大きくないと、県名が見えない。
df.plot(1, 2, kind='scatter', ax=ax)
for k, v in df.iterrows():
ax.annotate(v[0], xy=(v[1], v[2]), size=12) #v[0]に県名、v[1]が自民得票率、v[2]に持ち家比率が入っている。
plt.show()
ぱっとみると地方ほど持ち家比率が高そうなことが分かります。
相関係数を計算する
pandasは、corrメソッドを使うと簡単に計算できます。
こんな感じでした。
d.corr()
| 自民得票率 | 持ち家比率 | |
|---|---|---|
| 自民得票率 | 1.000000 | 0.638782 |
| 持ち家比率 | 0.638782 | 1.000000 |
相関係数はどれくらい確からしいのか?
求められた相関係数は、どれくらい確からしいのかを確認するために、検定を行います。
ここで、相関係数の検定として、フィッシャーのz変換を使います。
フィッシャーのz変換は、下記のようなものです。
フィッシャーのz変換
2次元正規母集団があるとき、母相関係数を$\rho$, 標本相関係数を$r$とするとき、
$$
z=\frac{1}{2}\log\frac{1+r}{1-r}
$$
$$
\eta=\frac{1}{2}\log\frac{1+\rho}{1-\rho}
$$
と変換する。
このとき、$z$の標本分布が、データ数$n$が多いとき、正規分布$N(\eta,1/(n-3))$となる。
したがって、$\sqrt{n-3}(z-\eta)$は、標準正規分布$N(0,1)$に従う。
実際に検定してみる。
i) 帰無仮説:母相関係数が0.0
$\rho=0.0$として、下記のようにpythonで計算します。
n=48 #データ数
r = 0.638782
rho = 0.0
z= 0.5*np.log((1+r)/(1-r))
eta = 0.5* np.log((1+rho)/(1-rho))
Z = np.sqrt(n-3)*(z-eta)
print("Z=",Z) #Z= 5.07216324479
一方、$Z_{0.025}=1.96$程度なので、明らかに$Z_{0.025} < Z$なので、仮説は棄却される。
よって相関がないとは言えない(有意水準0.05)
i) 帰無仮説:母相関係数が0.5
$\rho=0.5$として、i)と同じようにpythonで書いたらこんな感じです。
n=48 #データ数
r = 0.638782
rho = 0.5
z= 0.5*np.log((1+r)/(1-r))
eta = 0.5* np.log((1+rho)/(1-rho))
Z = np.sqrt(n-3)*(z-eta)
print("Z=",Z)
得られた、$z=1.39$について、$Z_{0.025}=1.96>1.39$より、帰無仮説を棄却しない。よって、母相関係数は0.5であるとしてよい。(有意水準0.05)
課題
本当は、geopandasとかを使って、日本地図に色を塗ったりしたかったのですが、win10でのインストールに失敗しました。
やり方が分かったら、再度挑戦します。
cf)正規標準分布のZをpythonではどう求める?
分布関数の面積が、$a$になるときの$Z$の値は、下記の関数で求めることができる
stats.norm.ppf(a)
今回は、両肩の優位水準0.05なので、下記のように求める。
stats.norm.ppf(1-0.025) #1.959963984540054
$Z_{0.025}=1.96$というのは、よく知られていると思いますが、上記の結果と同じぐらいですね。