はじめに
A. Mehta による Online Matching and Ad Allocation という書籍 (PDF) の輪読会の発表資料です。
以下の章・節の解説です。
-
- Online Bipartite Matching
- (3.1 と 3.2 は参考程度の解説)
- 本解説はこちらをご参照ください http://qiita.com/taketon_/items/92731d58c957d3b6d5ab
- 3.3 Known IID
-
- Online Vertex-Weighted Bipartite Matching
3. Online Bipartite Matching
Online Bipartite Matching の問題設定 (おさらい)
Tsubosaka さん資料 OnlineMatching勉強会第一回 も合わせて御覧ください。
- グラフ $G(U,V,E)$ は、既知の頂点の集合 $U$ と、オンラインで到着する頂点の集合 $V$ で構成される二部グラフである
- また、$E$ は、$U$ と $V$ の各頂点の間に引かれる辺 (エッジ) の集合である
- $U$ を広告主 (の広告)、$V$ をインプレッションと読み替えれば、次々に到着するインプレッションに対して、どの広告主マッチングさせるか、という問題に相当することが分かる
- 広告に関連する論文だと、 $U$ の代わりに $A$ を、 $V$ の代わりに $I$ を使って $G(A,I,E)$ と表現していることが多い?
-
$U$ と $V$ の頂点同士のマッチング結果 $M \subseteq E$ を最大化したい
- 広告の話に置き換えると、次々に到着するインプレッションに対して、可能な限り広告を割り当てたい、となる
- Online Bipartite Matching においては、「広告」は一度マッチング (配信) したら二度と配信できない、という扱いになる
3.1 Adversarial order
3.1.1 Deterministic Algorithms and Greedy
- Deterministic なアルゴリズムだと、競合比 $\frac{1}{2}$ を超えることはない
- Greedy アルゴリズムは競合比 $\frac{1}{2}$ を達成する
- Greedy アルゴリズム:
- オンラインで到着する頂点 $v \in V$ に対して、隣接している任意の頂点 $u \in U$ を選ぶ
- ランダムなアルゴリズムも競合比は $\frac{1}{2}$ がベストで、これを超えることはない
- ランダムアルゴリズム:
- オンラインで到着する頂点 $v \in V$ に対して、隣接している頂点の中からランダムに選ぶ
3.1.2 RANKING: An Optimal Algorithm
- 論文: An Optimal Algorithm for On-line Bipartite Matching
- R.M. Karp, U.V. Vazirani, and V.V. Vazirani.
- 競合比 $1 - \frac{1}{e} \simeq 0.63$ を達成する
- アルゴリズム:
0. 事前に、既知な頂点 $u_i \in U$ についてランダムに優先付けして並べておく
- $u_i$ のランクを $\pi(u_i)$ とする- オンラインで到着する頂点 $v_j \in V$ と隣接している頂点のうち、ランク $\pi(u)$ が一番高い $u_i \in U$ を選択する
- 以下は論文からのアルゴリズム部分の引用
Initialization: Pick a random permutation of the boy vertices
- thereby assigning to each boy a random priority or
ranking.
Matching Phase: As each girl arrives, match her to the
eligible boy (if any) of highest rank.
- ランダムになるので、競合比の期待値を計算することになる
- RANKING はすべての online algorithm の中で最適
3.2 Random order
- Greedy で $1-\frac{1}{e}$ の競合比を達成できる
- この競合比がベースラインになる
- Deterministic なアルゴリズムは、$\frac{3}{4}$ の競合比を超えることはない
- Randomized なアルゴリズムだと、$\frac{5}{6}$ の競合比
- RANKING は、$1-\frac{1}{e}$ を超える競合比となる
- 少なくとも、0.696 になる
3.3 Known IID
- 論文: Online Stochastic Matching: Beating 1 - 1/e
- 前節までは、最悪ケースやランダムに $v$ が到着するケースを考えてきた
- でも実際には、どのような種類の $v$ がどれくらいの確率で発生するかがわかっていることもある
- そこで、$v$ の種類 (type) の分布が既知であることを前提としたアルゴリズムを考える
- $\hat{V}$ を、「$v$ の種類」の集合とする
- $\hat{G}(U, \hat{V}, \hat{E})$ をベースグラフとする
- $\hat{v_i} \in \hat{V}$ が出現するであろう回数を $e_i$ とする
Suggested Matching (SM)
- 事前に (オフラインで) 最適と思われるマッチング $\mathcal{M}$ を求め、それをオンラインで利用する
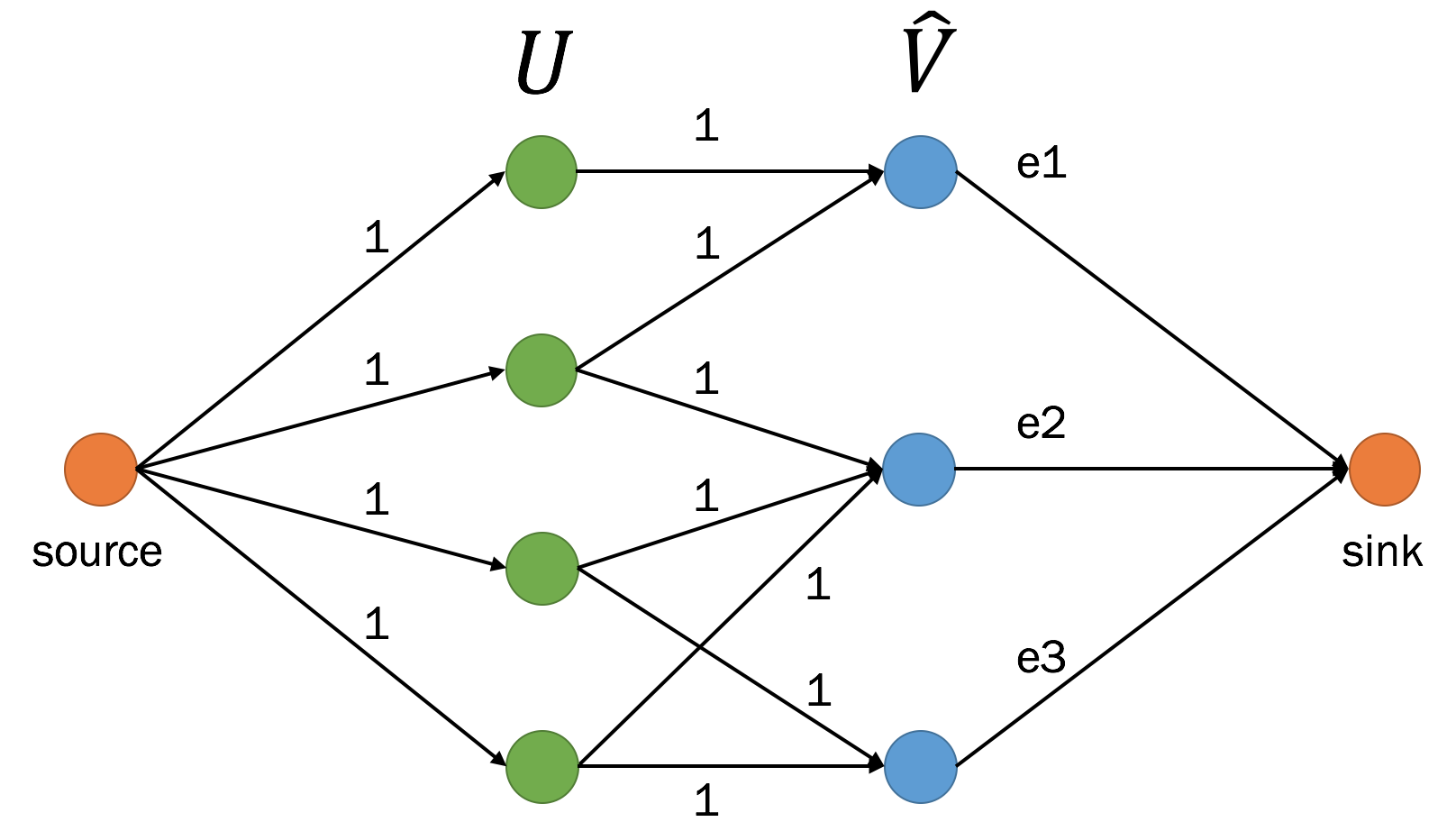
- 最適なマッチング $\mathcal{M}$ を求める問題は、ベースグラフ $\hat{G}$ から別のグラフ $G_f$ を構築し、この $G_f$ に対する最大フローを求める問題に置き換えられる
- つまりは、最大フロー問題のソルバーを利用すれば $\mathcal{M}$ は求められる、ということ
- $G_f$ の構築:
- source となる頂点 $s$ から頂点 $u_i \in U$ の間に辺 $(s, u_i)$ を張り、容量を 1 に設定する
- $\hat{v_j} \in \hat{V}$ から sink となる頂点 $t$ の間に辺 $(\hat{v_j}, t)$ を張り、容量を $e_j$ に設定する
- $\hat{E}$ に従って、$(u_i, \hat{v_j})$ の辺を張り、容量を 1 に設定する
- $G_f$ は、具体的にはこんな感じになる
- 最大フロー問題を解いた結果の辺 $(u, \hat{v})$ のフローを $f_{u\hat{v}} \in \{0, 1\}$ とする
- このアルゴリズムの競合比は $1-\frac{1}{e}$ となる
アルゴリズム
- Offline step
0. ベースグラフ $\hat{G}$ における、最適なマッチング $\mathcal{M}$ を、最大フロー問題を解くことで事前に求めておく - Online step
- オンラインで到着する頂点 $v \in V$ の種類を $\hat{v}$ とする
- $\mathcal{M}$ より、 $\hat{v}$ と隣接している $u \in U$ をピックアップする
- (書籍では明記されていないようだけど、元の論文では、$\frac{f_{{u}{\hat{v}}}}{e_j}$ の確率で $u$ をランダムに選択する、となっている)
- $u$ が過去にマッチングされた頂点でなければ、 $(u, v)$ をマッチング結果とする
Two Suggested Matching (TSM)
- Suggested Matching では、一つの最適マッチング結果をオフラインで求め、それをオンラインで利用していた
- この Suggested Matching には、すでにマッチング済みの $u \in U$ を何度もマッチングの対象として取り扱いうる問題がある
- Two Suggested Matching はその名の通り (?) 最適マッチング結果を $\mathcal{M}_1, \mathcal{M}_2$ の二つに分けて求め、それを Suggested Matching と同様にオンラインでのマッチングに用いる
- $\mathcal M_1, \mathcal M_2$ はそれぞれ互いに素 (disjoint) となるように求める
- 二つの最適マッチング結果を利用することで、The Power of Two Choices の要領で競合比を改善する
- $\mathcal M_1, \mathcal M_2$ を求めるために、 boosted flow graph を構築する
-
Boosted flow graph の構築:
- $(s, u_i)$ の容量を 2 に設定する
- $(u_i, \hat{v}_j)$ の容量を 1 に設定する
- $(\hat{v}_j, t)$ の容量を 2 に設定する
- $\mathcal M_1, \mathcal M_2$ を求めるアルゴリズムは論文を読んでください (書籍には明示されていない&論文読んでもちょっとよくわからなかった…)
- このアルゴリズムの競合比は約 0.67 となる
アルゴリズム
- Online step
- オンラインで到着する頂点 $v \in V$ の種類を $\hat{v}$ とする
- $\mathcal M_1$ より、 $\hat{v}$ と隣接している $u_1 \in U$ をピックアップし、まだマッチングがなければ $(u_1, v)$ をマッチング結果とする
- $\mathcal M_2$ より、 $\hat{v}$ と隣接している $u_2 \in U$ をピックアップし、まだマッチングがなければ $(u_2, v)$ をマッチング結果とする
その他のアルゴリズム
TSM をベースとするアルゴリズム
-
Improved Bounds for Online Stochastic Matching
- Two Suggested Matching を一般化した d-Suggested Matching
- Online stochastic matching: Online actions based on offline statistics
TSM とは異なるアルゴリズム
- Online stochastic weighted matching: Improved approximation algorithms
-
Online Stochastic Matching: New Algorithms with Better Bounds
- 現時点で最良のアルゴリズムらしい
4. Online Vertex-Weighted Bipartite Matching
問題設定
- Online Bipartite Matching と同じく、二部グラフ $G(U,V,E)$ を取り扱う、
- ただし Online Bipartite Matching とは異なり、頂点 $u \in U$ に非負の重み $w_u$ が付与されている
- この重みは $U$ と同様に事前に明らかになっている
- マッチング結果 $M \subseteq E$ でマッチングされた $u \in U$ の重みの合計値 $\sum_u w_u$ を最大化したい
4.1 Adversarial Order
- Online Bipartite Matching で取り扱っていた二つのアルゴリズム Greedy と Ranking の両者を Online Vertex-Weighted Bipartite Matching でも考えてみる
- Greedy アルゴリズム
- オンラインで到着する頂点 $v \in V$ に対して、重み $w_u$ が最大の頂点 $u \in U$ を選ぶ
- この Greedy アルゴリズムは、重みに偏りがある場合にうまく働く
- その一方で、重みの偏りがなく、どの重みも同じ場合には $1/2$ の競合比にしかならない
- Ranking アルゴリズム
- 重み $w_u$ を無視して、Online Bipartite Matching と同様に取り扱う
- この Ranking アルゴリズムは、重みがどれも同程度の場合にうまく働く
- その一方で、重みに偏りがある場合は $1/2$ の競合比にしかならない
- この Online Vertex-Weighted Bipartite Matching においては、Greedy と Ranking の両者を合わせた hybrid なアルゴリズムが必要になる
Ranking アルゴリズムの一般化
- Greedy アルゴリズムでは重み $w_u$ の一番大きい頂点 $u \in U$ を選択していた
- ここで、$w_u$ の代わりに、ゆらぎを乗じた重み $\tilde{w}_u$ の一番大きい頂点を選択するようにしてみる
- $\tilde{w}_u$ の計算は次のとおり
\tilde{w}_u = w_u \psi(r_u) \\
\psi(x) = 1 - e^{x-1} \\
r_u \sim \mathcal{U}[0,1]
- $r_u$ は一様分布 $\mathcal{U}[0,1]$ から生成した乱数
- 次のアルゴリズムの競合比は $1 - \frac{1}{e}$ となる
Perturbed Greedy アルゴリズム
- Offline step:
- 頂点 $u \in U$ ごとに、$[0, 1]$ の範囲の一様乱数 $r_u$ を生成する
- $\tilde{w}_u = w_u \psi(r_u)$ として、ゆらぎを乗じた重みを計算する
- Online step
- オンラインで到着する頂点 $v \in V$ に対して、ゆらぎを乗じた重み $\tilde{w}_u$ が最大の頂点 $u \in U$ を選ぶ
4.2 Known IID
- (先ほども掲示した) 次の論文でアルゴリズムが提案されている