今年は, 素数が大流行の兆し!
オフィスの給湯室ではディオフォントス方程式がどうとかで盛り上がっているし, 先日も 6 歳の娘に「29は素数だよね? パパ」と聞かれて「えーと (7x7=49 は 29 より大きい, 7 より小さい素数 2, 3, 5 で割り切れないから) そ, そうだね, 素数だねー.」なんて会話が.
ということで, 私も流行に乗って, 素数について改めて考え直してみました.
そこそこ速く大きな素数まで, 最適化のために意味的な綺麗さをあまり犠牲にせずに 2 から始まる昇順の素数列を求めたい!
そんなあなたのために, 以下のコードを捧げます.
Clojure 版
Clojure で素数列の定義を書きますと,
(def prime-numbers
((fn f [x]
(cons x
(lazy-seq
(f (first
(drop-while
(fn [n]
(some #(zero? (mod n %))
(take-while #(<= (* % %) n) prime-numbers)))
(iterate inc (inc x))))))))
2))
のようになります.
素数列は『見つかっているうちの最後の素数 x を与えると「自分自身 f に, x の次の素数を与えて得られる遅延シーケンス (lazy-seq ...)」 の先頭に x を付加するような関数 f』に 2 を与えたもの.
ただし x の次の素数は, x より 1大きい数から, 1ずつ大きくなる数列 (iterate ...) の要素を, 『自然数 n を与えると, 素数列 prime-numbers の先頭から, 二乗が n 以下である間, 要素を取り出した列 (take-while ...) の中に n を割り切るものがあれば真を返すような関数 (fn [n] ...)』に与えて, 真を返す間の要素を捨てたもの (drop-while ...) の最初の要素 (first ...) です.
素数列を求めるのに素数列を使っていますが, 次の素数の候補に対して, 二乗がその数以下であるような素数までは求まっているので, 大丈夫.
遅延シーケンス万歳!
Clojure 版の使い方
そのまま表示しようとするとメモリの許す限り表示を続けます.
スタックは消費しませんが, ヒープにそれまでに求まった素数を覚えています.
user=> prime-numbers
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117^C
2から昇順 100個の素数
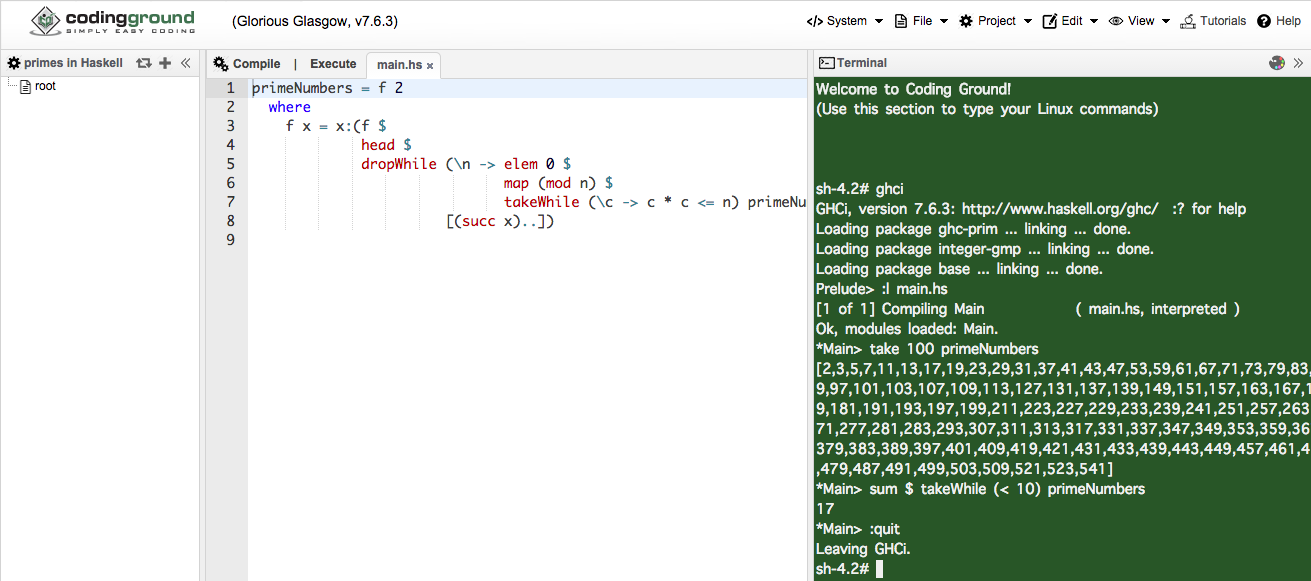
user=> (take 100 prime-numbers)
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541)
100未満の素数
user=> (take-while #(< % 100) prime-numbers)
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97)
9000以上, 10000 未満の素数
user=> (take-while #(< % 10000) (drop-while #(< % 9000) prime-numbers))
(9001 9007 9011 9013 9029 9041 9043 9049 9059 9067 9091 9103 9109 9127 9133 9137 9151 9157 9161 9173 9181 9187 9199 9203 9209 9221 9227 9239 9241 9257 9277 9281 9283 9293 9311 9319 9323 9337 9341 9343 9349 9371 9377 9391 9397 9403 9413 9419 9421 9431 9433 9437 9439 9461 9463 9467 9473 9479 9491 9497 9511 9521 9533 9539 9547 9551 9587 9601 9613 9619 9623 9629 9631 9643 9649 9661 9677 9679 9689 9697 9719 9721 9733 9739 9743 9749 9767 9769 9781 9787 9791 9803 9811 9817 9829 9833 9839 9851 9857 9859 9871 9883 9887 9901 9907 9923 9929 9931 9941 9949 9967 9973)
10未満の素数の総和
user=> (apply + (take-while #(< % 10) prime-numbers))
17
200万未満の素数の総和
user=> (time (apply + (take-while #(< % 2000000) prime-numbers)))
"Elapsed time: 6372.194 msecs"
6.4秒 (手元の MacBook Pro) で求まりました. (求まった和そのものは掲載しないでおきます.)
Clojure の実行環境が手元にないよ
って人には Coding Ground があります.
プロジェクト作っておいたので primes in Clojure へ行って, teminal に (take 100 prime-numbers) とか入れてみてください.
こんな感じ
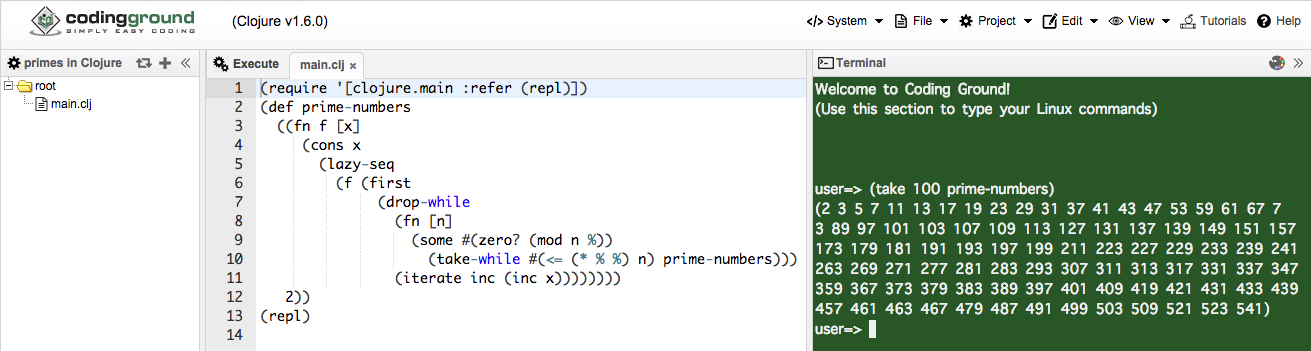
で実行してみることができます.
REPL 抜けるのは (System/exit 0).
Haskell 版
「動的型の言語はよく分からないです. Haskell なら分かるんですけど...」というあなた. Google 翻訳で元言語に Clojure, 翻訳先に Haskell を指定して, 上記のコードを貼付けてみてください.
選べない?
ふーん. まだ対応してなかったのか.
では, Clojurian の拙い翻訳で申し訳ないですが, 下記で意図を汲み取ってください.
primeNumbers = f 2
where
f x = x:(f $
head $
dropWhile (\n -> elem 0 $
map (mod n) $
takeWhile (\c -> c * c <= n) primeNumbers)
[(succ x)..])
Haskell の開発環境がないよ
って人. Coding Ground のプロジェクト primes in Haskell へ行って, ghci 立ち上げて, :l main.hs して, take 100 primeNumbers とか sum $ takeWhile (< 10) primeNumbers とか, 入力してみてください.
GHCi を抜けるのは :quit です.
これであなたも素数通の仲間入りですね!
--
二年くらい前に書いたもの -> Project Euler Problem 10 解答とコメント