マンデルブロ集合

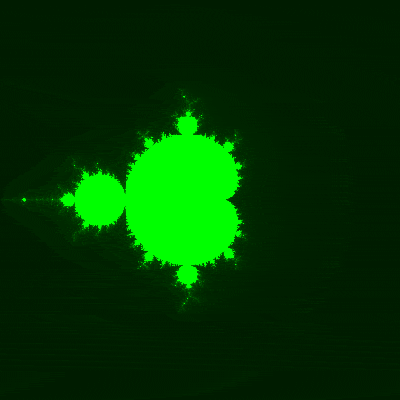
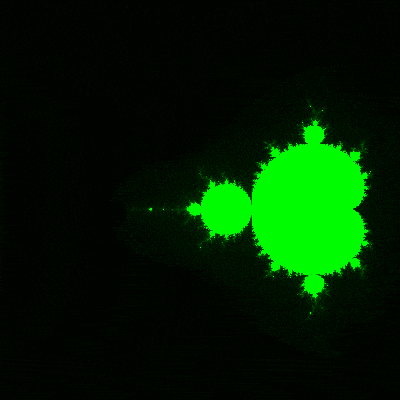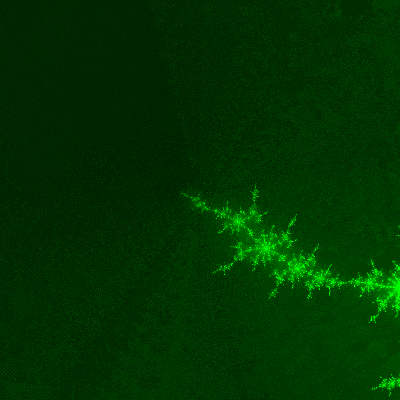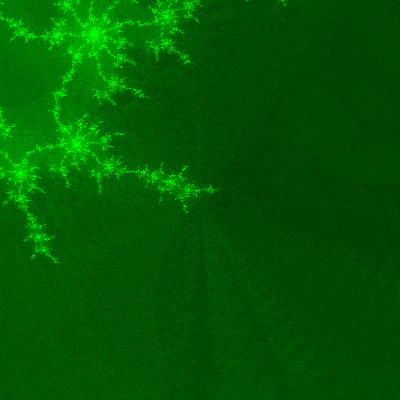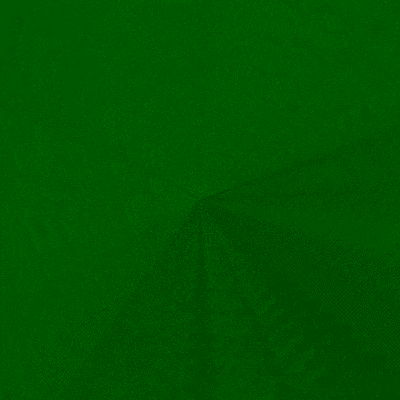
有名なフラクタル。
複素数cを二次元グラフにxとyとしてマップしてあげると描写できます。

描写

根本はz ** 2 + cという単純な式。
発散をinfinite?,nan?で判断。 （追記参照）
発散するまでにかかったループ数も色付け用に返しておきます。

def mandelbrot?(z,c,nn)
  for n in 1 .. nn
    z = z ** 2 + c
    if z.real.infinite? || z.real.infinite? || z.imag.infinite? || z.imag.nan?
      return [false, n]
    end
  end
  [true, n]
end

require "rmagick"
def make_gif
  il = Magick::ImageList.new
  il.new_image(400,400)

  cs = -2.step(2,0.009).to_a
  cs = cs.product(cs)

  for y,x in cs
    m = mandelbrot?(Complex(0,0),Complex(x,y),100)
    c = 65535/100*m[1]
    il.pixel_color(200+100*x,200+100*y,Magick::Pixel.new(0,c,0))
  end
  il.write("mandelbrot.gif")
end

make_gif

拡大

フラクタルの醍醐味。
どこまで拡大していっても自分自身で自分を構成している。
拡大点の調整に苦労。
アニメーションGIFはnew_imageでフレームを追加していける。

def make_animation_gif(my,mx,d,fs)
  il = Magick::ImageList.new

  scale = 1
  cs = -2.step(2,d).to_a
  cs = cs.product(cs)

  for n in 1 .. fs
    il.new_image(400,400) {
      self.background_color = "black"
    }
    #il.annotate(Magick::Draw.new, 1,1, 30,30, "scale = #{scale}")

    for y,x in cs
      cy = scale * y + my
      cx = scale * x + mx
      m = mandelbrot?(Complex(0,0),Complex(cx,cy),100)
      c = 65535/100*m[1]
      il.pixel_color(200+100*x,200+100*y,Magick::Pixel.new(0,c,0))
    end

    scale = scale * 0.9
    p n
    il.write("mandelbrot.gif")
  end
end

make_animation_gif(-0.09445, -1.264405, 0.009, 150)

（若干ずれてる）

遅い

私のPC(MacBook Air mid 2013, Intel Core i5 1.3 GHz, 4 GB, Intel HD Graphics 5000 1536 MB)
400x400x150のGIF生成に32分かかりました。
一フレームあたり13秒です。
rubyでやるもんじゃないね。

追記

@scivolaさんのコメントを元に修正。ご指摘ありがとうございます。
数学の素養が無いので数式読み取れているか自信が無いです。
GIF生成に32分かかっていたのが26分に短縮。素晴らしい。

def mandelbrot?(z,c,nn)
  for n in 1 .. nn
    z = z ** 2 + c
    #if z.real.infinite? || z.real.infinite? || z.imag.infinite? || z.imag.nan?
    if z.abs > 2
      return [false, n]
    end
  end
  [true, n]
end

make_animation_gif(-0.09445, -1.264405, 0.009, 150)

（やっぱりズレてる）

再追記

@scivolaさんに再ツッコミいただきました。ありがたいです。
確かに膨大な数のオブジェクト生成ですもんね。良い倹約です。
timeコマンドで比べて見ました。

修正前
ruby mandelbrot.rb 1539.25s user 6.27s system 99% cpu 25:52.61 total
ruby mandelbrot.rb 1616.53s user 11.18s system 98% cpu 27:24.23 total

修正後
ruby mandelbrot.rb 1520.56s user 6.73s system 99% cpu 25:34.62 total
ruby mandelbrot.rb 1500.12s user 4.67s system 99% cpu 25:10.53 total

少々早くなりましたが、これだけバラツキがあると誤差っぽい気も。

def make_animation_gif(my,mx,d,fs)
  il = Magick::ImageList.new

  scale = 1
  cs = -2.step(2,d).to_a
  cs = cs.product(cs)
  palette = []
  1.upto(100) do |n|
    c = 65535 / 100 * n
    palette[n] = Magick::Pixel.new(0, c, 0)
  end

  for n in 1 .. fs
    il.new_image(400,400) {
      self.background_color = "black"
    }

    for y,x in cs
      cy = scale * y + my
      cx = scale * x + mx
      m = mandelbrot?(Complex(0,0),Complex(cx,cy),100)
      il.pixel_color(200+100*x,200+100*y,palette[m[1]])
    end

    scale = scale * 0.9
    p n
    il.write("mandelbrot_abs_zoom.gif")
  end
end