乗り遅れた。
zundoko[x_, y_, z_] := Append[#,z]&@NestWhile[Append[#,RandomChoice@{x,y}]&,{},!MatchQ[#,{___,Repeated[x,{4}],y}]&];
In[] = zundoko[ズン","ドコ","キ・ヨ・シ!"]
Out[] = {"ドコ", "ズン", "ズン", "ドコ", "ドコ", "ドコ", "ズン", "ドコ", "ドコ", "ズン", "ドコ",
"ドコ", "ズン", "ズン", "ズン", "ドコ", "ドコ", "ドコ", "ズン", "ドコ", "ズン", "ドコ",
"ズン", "ドコ", "ドコ", "ドコ", "ズン", "ドコ", "ドコ", "ズン", "ドコ", "ズン", "ズン",
"ズン", "ズン", "ドコ", "キ・ヨ・シ!"}
ズンドコ過程の数理
最後のキヨシを除いて、ズンドコ過程で得られる配列は{...,"ズン","ズン","ズン","ズン","ドコ"}。
この配列の長さが$n$である確率を$P_n$とする。
最初の"ドコ"が(1|2|3|4)番目に現れる長さ$n$で過程が終わる確率を$A_n$,$B_n$,$C_n$,$D_n$とする。
ドコが1度だけしか現れずに、長さ$n$で過程が終わる確率を$O_n$とする。
(注: 以前の版では$O_n$を忘れていた。恥ずかしい。)
$P_n = O_n + A_n + B_n + C_n + D_n$
$O_n = 2^{-n}$
$A_n = \frac{1}{2}(O_{n - 1} + A_{n - 1} + B_{n - 1} + C_{n - 1} + D_{n - 1}) = \frac{1}{2}P_{n - 1}$
$B_n = \frac{1}{2}A_{n - 1}$
$C_n = \frac{1}{2}B_{n - 1}$
$D_n = \frac{1}{2}C_{n - 1}$
というマスター方程式が立つ。
あとはこれを整理すれば$P_n = P_{n - 1} - \frac{1}{32} P_{n - 5}$となり、$P_1 = P_2 = P_3 = P_4 = 0, P_5 = \frac{1}{32}$の境界条件での解は
$P_n = \alpha_1^n\beta_1+\alpha_2^n\beta_2+\alpha_3^n\beta_3+\alpha_4^n\beta_4 - \frac{1}{3 \cdot 2^n}$
となる。
$\alpha_i$は$16 x^4 - 8 x^3 - 4 x^2 -2x - 1$の根で
$\alpha_1 \approx -0.387$
$\alpha_2 \approx 0.964$
$\alpha_3 \approx -0.0382 - 0.408 i$
$\alpha_4 \approx -0.0382 + 0.408 i$
$\beta_i$は$1689 x^4 + 1126 x^3 + 232 x^2 + 10 x - 1$の根で
$\beta_1 \approx -0.234$
$\beta_2 \approx 0.044$
$\beta_3 \approx -0.239 - 0.019 i$
$\beta_4 \approx -0.239 + 0.019 i$
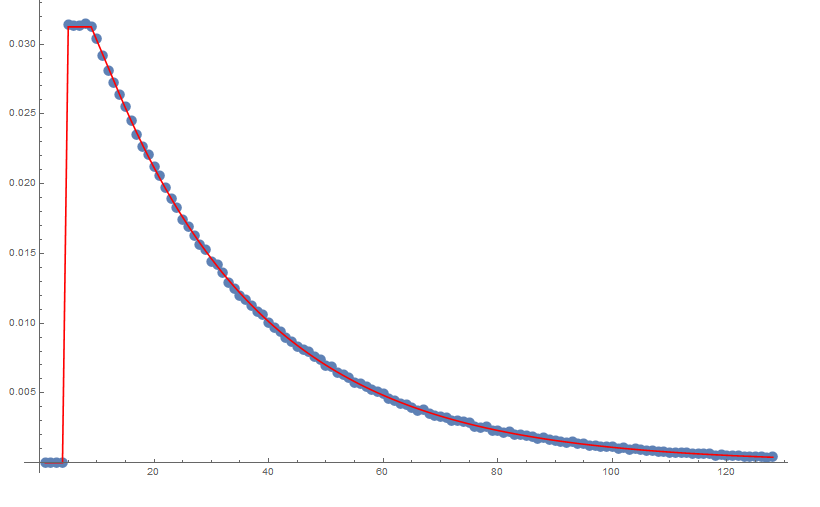
実際、サンプリングして$P_n$を推定するとよく一致する。
ズンドコ過程の漸近形
$n \rightarrow \infty$での$P_n$の漸近形は$P_n \approx \alpha_2^n \beta_2$
$\alpha_2$は$0.9637809877...$と$1$に近く、非常に収束が遅い。
また、$\alpha_1$の減衰モードもわりと遅い。
誤って導きがちな偽の漸近形$(1-2^{-5})^n = (31/32)^n$を、サンプリングに基づいて棄却しようとすると、かなりの数のサンプリングが必要になる。
ズンドコ過程の平均長と分散
$a_0 = \frac{1}{2}$, $b_0 = -\frac{1}{3}$とすると、$P_n = \sum_{i = 0}^{5} a_i^n b_i$
ズンドコ過程の平均長は
$E[n] = \sum_{n = 1}^{\infty} n P_n = \sum_{i = 0}^{5} \frac{a_i b_i}{(1 - a_i)^2} = 31.98354688...$
ズンドコ過程の長さの分散は
$E[n^2] = \sum_{n = 1}^{\infty} n^2 P_n = \sum_{i = 0}^{5} \frac{a_i(a_i + 1) b_i}{(1 - a_i)^3}$
$E[n^2]-(E[n])^2 = 737.0537700...$