回転楕円体面上（地球表面上）の正多角形

こんにちは。
回転楕円体面上（地球表面上）の「正多角形と言えるもの」を求める計算を考えてみました。GeographicLib を利用すれば簡単で、JavaScript で書いてみました¹。

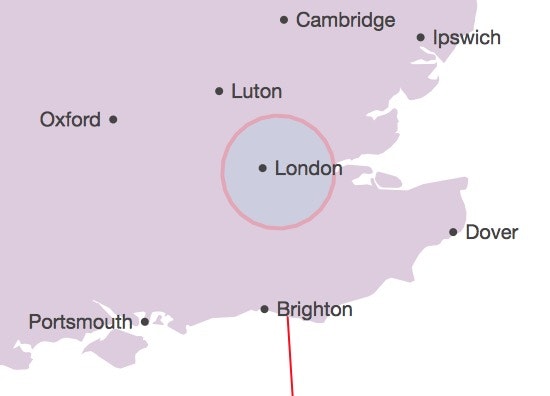
なお下図は、これの応用として半径 30 km の円を近似的に描いた例です（d3.js を使用）。

geoRegularPolygon.js

#!/usr/bin/env jsc
// /System/Library/Frameworks/JavaScriptCore.framework/Versions/A/Resources/jsc

var GeographicLib = require("geographiclib"), geod = GeographicLib.Geodesic.WGS84;

// regular polygon on a map
// radius of a circumscribed circle 
function geoRegularPolygon(center, radius, nVertices) {
    for (var i=0, poly=[], dir; i < nVertices; i++) {
        dir = 90 - i*360/nVertices
        r = geod.Direct(center[1], center[0], dir, radius);
        poly.push([r.lon2, r.lat2]);
    }
    poly.push(poly[0]);
    return poly;
}

var nVertices = 36, radius = 100, center = [-0.001473, 51.477933];
var i = 0;
while (i < arguments.length) {
    switch (arguments[i]){
      case "--lonlat":
        center[0] = Number(arguments[++i]);
        center[1] = Number(arguments[++i]);
        break;
      case "--radius":
        radius = Number(arguments[++i]);
        break;
      case "--nVertices":
        nVertices = Number(arguments[++i]);
        break;
    }
    i++;
}

var poly = geoRegularPolygon(center, radius, nVertices);
for (i = 0; i < poly.length; i++) {print(center.join(" "), poly[i].join(" "));} 

quit();

###近似計算
次に、これの近似計算版を考え²、近似精度評価してみました（GeographicLib の GeodSolve 計算と比較）。中心点から多角形頂点への方位角と距離の誤差です。

ここでは中心点経緯度 [-0.001473, 51.477933]、radius= 1 km の場合で、距離誤差の最大はおよそ 0.1 mm でした。この近似では、距離誤差はradiusの二乗に比例します。

geoRegularPolygon.js

const DEG = Math.PI/180;
const RE = 6378137.0;
const FE = 1/298.257223563;
const E2 = FE*(2-FE)

// radius of a circumscribed circle 
geoRegularPolygonApproximated(center, radius, nVertices) {
    var cs=[Math.cos(Math.PI*2/nVertices),Math.sin(Math.PI*2/nVertices)];
    var coslatc=Math.cos(center[1]*DEG), sinlatc=Math.sin(center[1]*DEG);
    var u2=1-E2*sinlatc*sinlatc, u=Math.sqrt(u2);
    var nm=[u/coslatc, u*u2/(1-E2), 1.5*u*E2/(1-E2)*coslatc*sinlatc*DEG];
    for (var i=0, poly=[], xy=[radius/RE/DEG,0.0], lon, lat;;) {
        q = xy[1]*(nm[1]-nm[2]*xy[1]);
        lon = center[0]+xy[0]*nm[0]*(1+sinlatc/coslatc*q*0.5*DEG);
        lat = center[1]+q;
        poly.push([lon, lat]);
        if (++i >= nVertices) {poly.push(poly[0]);break;}
        xy = [xy[0]*cs[0]-xy[1]*cs[1], xy[1]*cs[0]+xy[0]*cs[1]];
    };
    return poly;
}

$ RADIUS=1000
$ ./geoRegularPolygon.js -- --radius $RADIUS --nVertices 12 | xargs -I @ sh -c "echo @ | GeodSolve -i -w -p 6 | awk '{printf(\"%9.3f%12.6f\n\",\$1,\$3-${RADIUS})}'"
   89.994   -0.000002
   59.995    0.000092
   29.997    0.000052
    0.000    0.000000
  -29.997    0.000052
  -59.995    0.000092
  -89.994   -0.000002
 -119.995   -0.000101
 -149.997   -0.000060
 -180.000    0.000000
  149.997   -0.000060
  119.995   -0.000101
   89.994   -0.000002
$

###応用例
地図上で正多角形を描くことに使えそうです（d3.js を使用）。radius= 30 km の例です（冒頭図）。

var KM = 1000, poly = geoRegularPolygon([-0.001473, 51.477933], 30*KM, 36);
// d3.js
svg.selectAll("polygon")
    .data([poly])
    .enter().append("polygon")
    .attr("points",function(d) { 
        return d.map(function(d) {
            return projection(d).join(",");
        }).join(" ");
     })
    .attr("fill","skyblue")
    .attr("opacity",0.2)
    .attr("stroke","red")
    .attr("stroke-width",2);

---

1. 「OSXのターミナルでJavascriptを動かす」 ↩

2. 「地理経緯度の変換式」など ↩