概要
スパースモデリング第5章の数値例をPythonで実装.
コードと実験結果をまとめたJupyter notebook.
導入
5章では観測データに雑音を含む場合を扱う.観測データに雑音を含むため誤差項の制約を$\epsilon$以下に弱める.
$$ (P_{0}^{\epsilon}): \min_{\mathbf{x}} ||\mathbf{x}||_{0} \text{ subject to } ||\mathbf{b}-\mathbf{Ax}|| _{2} \leq \epsilon $$
- 直交マッチング追跡(OMP)では,単に反復計算の停止条件$\epsilon_{0}=\epsilon$として解を求めれば良い.
$\ell_{0}$ノルムを$\ell_{1}$ノルムに緩和すると$(P_{1})$の変形版である基底追跡ノイズ除去(basis pursuit denoising; BPDN)が得られる.
$$ (P_{1}^{\epsilon}): \min_{\mathbf{x}} ||\mathbf{x}||_{1} \text{ subject to } ||\mathbf{b}-\mathbf{Ax}|| _{2} \leq \epsilon $$
適切なラグランジュ乗数$\lambda$に対して,$ (P_{1}^{\epsilon})$の解は以下の制約なし最適化問題の解と一致する.
$$ (Q_{1}^{\lambda}): \min_{\mathbf{x}} \lambda ||\mathbf{x}||_{1} + \frac{1}{2} ||\mathbf{b}-\mathbf{Ax}|| _{2} $$
$(Q_{1}^{\lambda})$を解く簡単な方法は,反復重み付け最小2乗法(iterative-reweighted-least-squares; IRLS)である.
$\mathbf{X}=\rm{diag}(\mathbf{|x|})$とすると$ ||\mathbf{x}||_{1} = \mathbf{x}\mathbf{X}^{-1}\mathbf{x}$となる.つまり$\ell_{1}$ノルムは(重み付き)2乗$\ell_{2}$ノルムと見なすことができる.現在の近似解$\mathbf{x_{\rm{k-1}}}$が与えられたら,$\mathbf{X_{\rm{k-1}}}=\rm{diag}(\left|\mathbf{x_{\rm{k-1}}}\right|)$とおいて以下の問題を解く.
$$ (M_{k}): \min_{\mathbf{x}} \lambda \mathbf{x^{\rm{T}}} \mathbf{X^{\rm{-1}}} \mathbf{x} + \frac{1}{2} || \mathbf{b} - \mathbf{Ax} ||_{2}^{2} $$
よってIRLSのアルゴリズムは現在の重み$\mathbf{X_{\rm{k-1}}}$を用いて$\mathbf{x_{k}}$を得た後,$\mathbf{x_{k}}$を用いて$\mathbf{X_{\rm{k}}}$を得ることを交互に繰り返して近似的に$(Q_{1}^{\lambda})$の解を得るものとなる.5章は主に$(Q_{1}^{\lambda})$を近似的に解くIRLSの説明と,LARS(least angle regression stagewise; 最小角回帰)の概略からなる.
IRLSアルゴリズム
初期化
$k=0$として
- (任意の)初期解 $\mathbf{x_{\rm{0}}}=\mathbf{1}$
- 初期重み行列 $\mathbf{X_{\rm{0}}}=\mathbf{I}$
メインループ
$k \leftarrow k + 1$として,以下のステップを実行する.
-
正則化付き最小2乗:以下の線形連立方程式$$ \left(2\lambda\mathbf{X_{\rm{k-1}}^{\rm{-1}}} + \mathbf{A^{\rm{T}}A}\right) \mathbf{x} = \mathbf{A^{\rm{T}}b}$$を反復法を用いて解き,近似解$\mathbf{x_{\rm{k}}}$を得る.教科書では数回の共役勾配法の反復で十分であると記載されている.本検討ではscipy.optimize.minimizeを使用.
-
重みの更新:$\mathbf{x_{\rm{k}}}$を用いて$X_{k}(j,j)=|x_{k}(j)|+\epsilon$として重み対角行列$\mathbf{X}$を更新する.
-
停止条件:もし$||\mathbf{x_{\rm{k}}}-\mathbf{x_{\rm{k-1}}}||_{2}$が事前に与えられたしきい値よりも小さければ終了し,そうでなければ反復する.
実験
シミュレーション
$\mathbf{x}$ 200次元のベクトル
$\mathbf{b}$ 100次元のベクトル
$\mathbf{A}$ 100×200次元の行列,$[-1, 1)$の一様乱数を列正規化
- $\mathbf{x}$の非ゼロの要素数$k=4$として、その非ゼロ要素の値を$[-2, -1] \cup [1, 2]$の範囲の一様分布からiid抽出する.
- 標準偏差$\sigma=0.1$のガウス分布からiid抽出した加法ノイズ$\mathbf{e}$を用いて,$\mathbf{b}=\mathbf{Ax}+\mathbf{e}$を計算する.
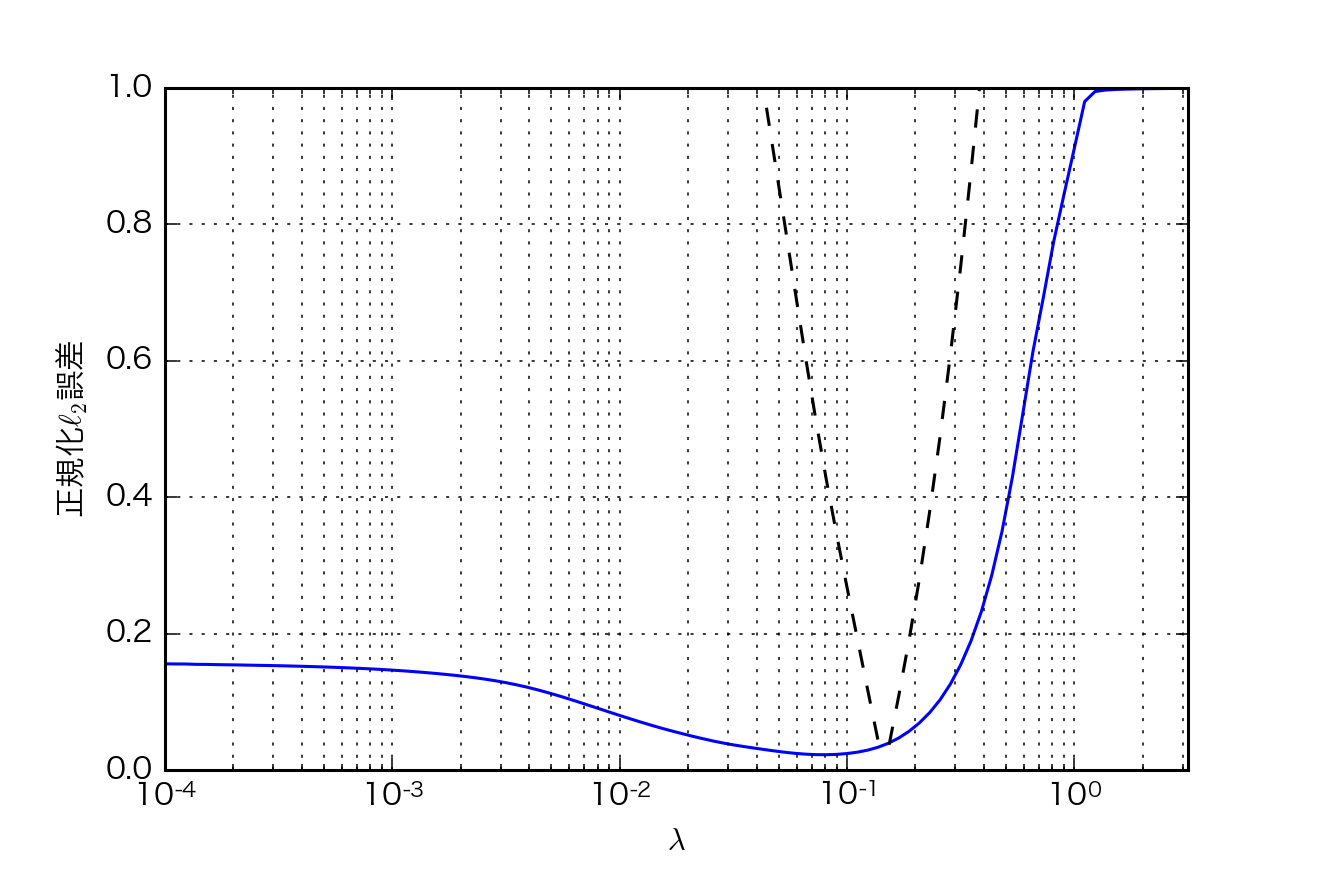
解決すべき課題の1つは$\lambda$の値をどのように決めるかである.ここでは経験則に従って,$\sigma$と非ゼロ要素の標準偏差の比に近い値を$\lambda$とする.非ゼロ要素の標準偏差はおよそ2なので,$\sigma/2=0.05$付近の値を$\lambda$とする.
結果
- $\lambda$の値を変えながら得られた解を$ \frac{|| \hat{\mathbf{x_{\rm{\lambda}}}} - \mathbf{x_{\rm{0}}} ||}{||\mathbf{x_{\rm{0}}}||} $で評価した.IRLSの反復回数は100回とした.
破線は$\left|\log\left(||\mathbf{A\hat{x_{\rm{\lambda}}}}-\mathbf{b}||^{2}/\left(n\sigma^{2}\right)\right)\right|$の値を示しており,$\lambda$がどの値の時に残差$||\mathbf{A\hat{x_{\rm{\lambda}}}}-\mathbf{b}||$がノイズのパワー$n\sigma^{2}$と同程度になるのかを表している.これは$\lambda$の値を決める別の経験則である.
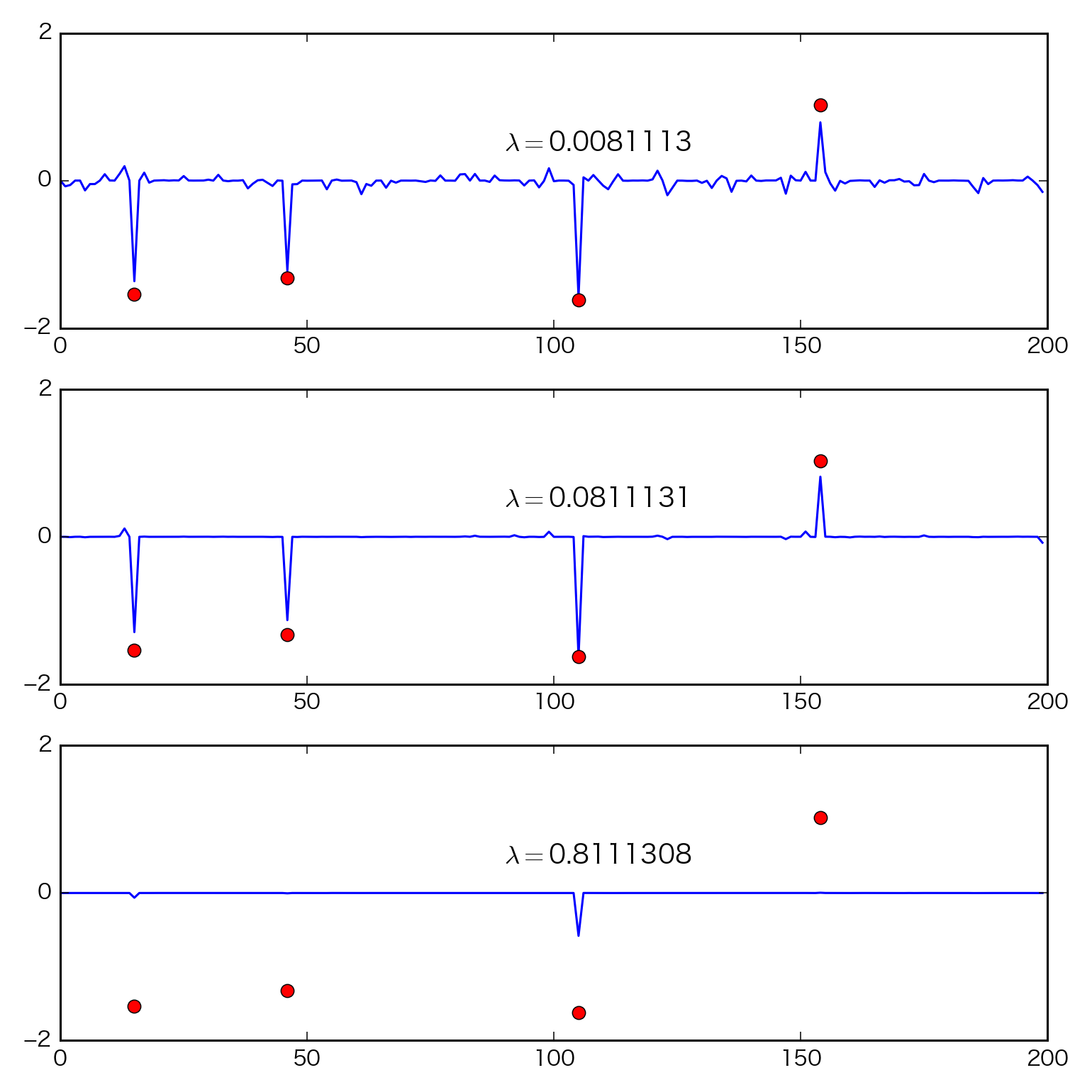
- 最も良い$\lambda$の値を用いた場合と,それより大きい値,小さい値を用いた場合の,三つの解
真の解$\mathbf{x_{\rm{0}}}$(赤丸)と比較すると,最適な$\lambda$の値を用いた場合が,$\mathbf{x_{\rm{0}}}$の非ゼロ要素の位置を最も良く復元している.$\lambda$の値が小さい場合は解は密に,大きい場合は疎になる.
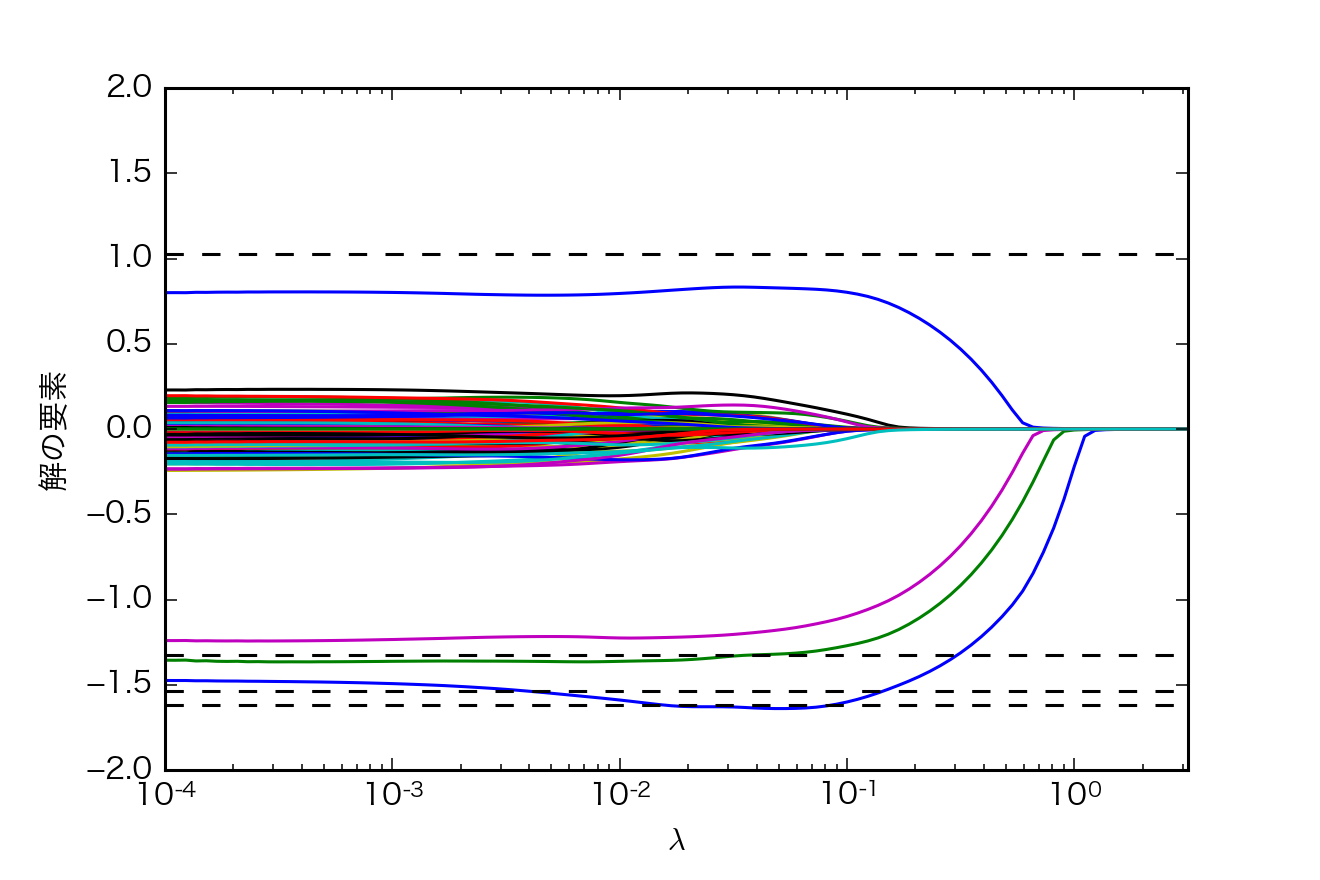
- 一つのグラフの中に,すべての$\lambda$に対する解を一度に表示
各プロットは$\mathbf{x}$の一つの要素の$\lambda$に対する値を示している.破線は$\mathbf{x_{\rm{0}}}$の値である.
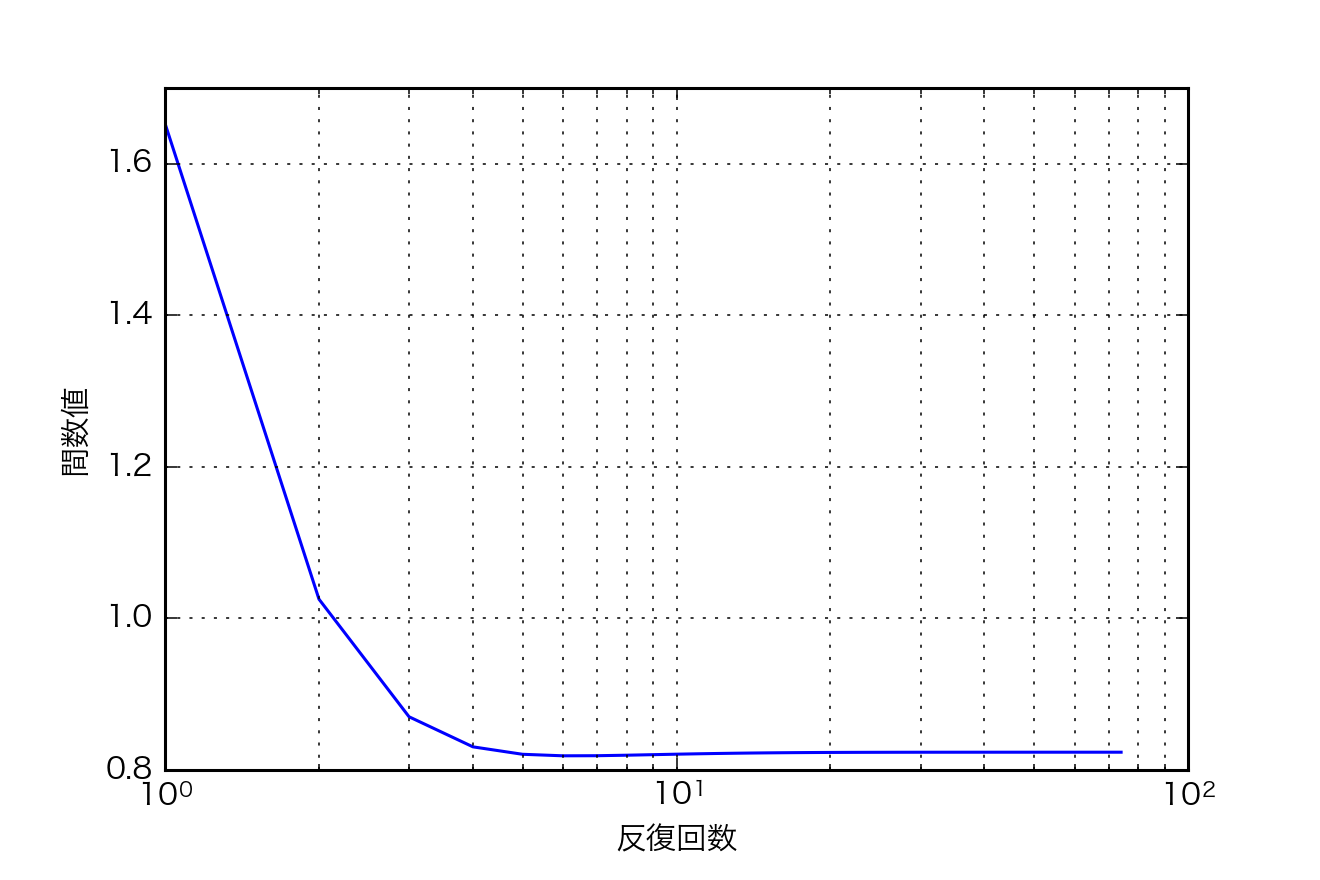
- 最適な$\lambda$を用いた場合の,IRLSの反復回数に対する関数値$(\lambda||\mathbf{x}||_{1}+\frac{1}{2}||\mathbf{b}-\mathbf{Ax}||)$
LARSアルゴリズム
- イマイチ理解できなかったのでsklearnのLassoLarsを用いて実験のみ
実験
シミュレーション
$\mathbf{x}$ 50次元のベクトル
$\mathbf{b}$ 30次元のベクトル
$\mathbf{A}$ 30×50次元の行列,$[-1, 1)$の一様乱数を列正規化
- $\mathbf{x}$の非ゼロの要素数kとして、その非ゼロ要素の値を$[-2, -1] \cup [1, 2]$の範囲の一様分布からiid抽出する.
- 標準偏差$\sigma=0.1$のガウス分布からiid抽出した加法ノイズ$\mathbf{e}$を用いて,$\mathbf{b}=\mathbf{Ax}+\mathbf{e}$を計算する.
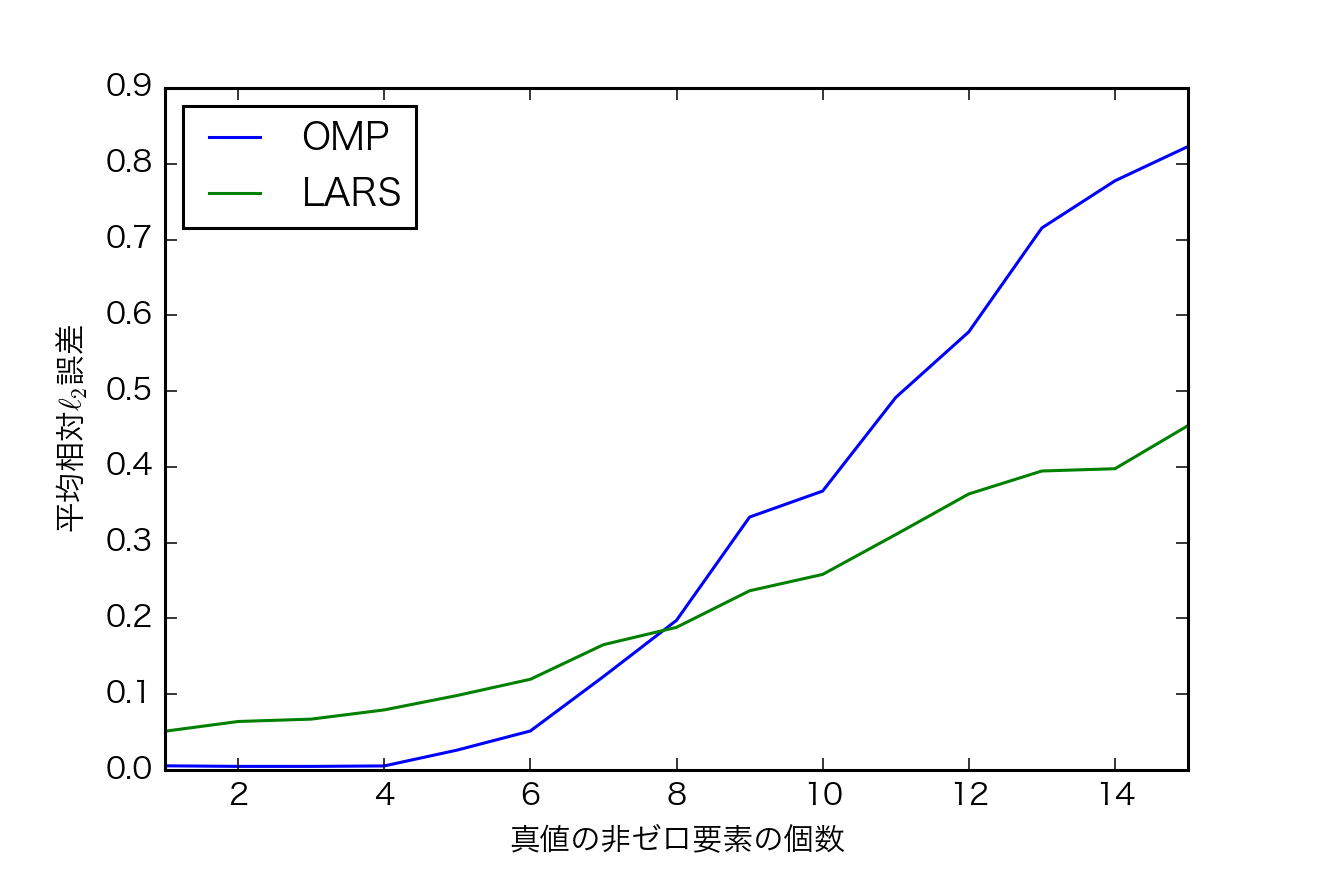
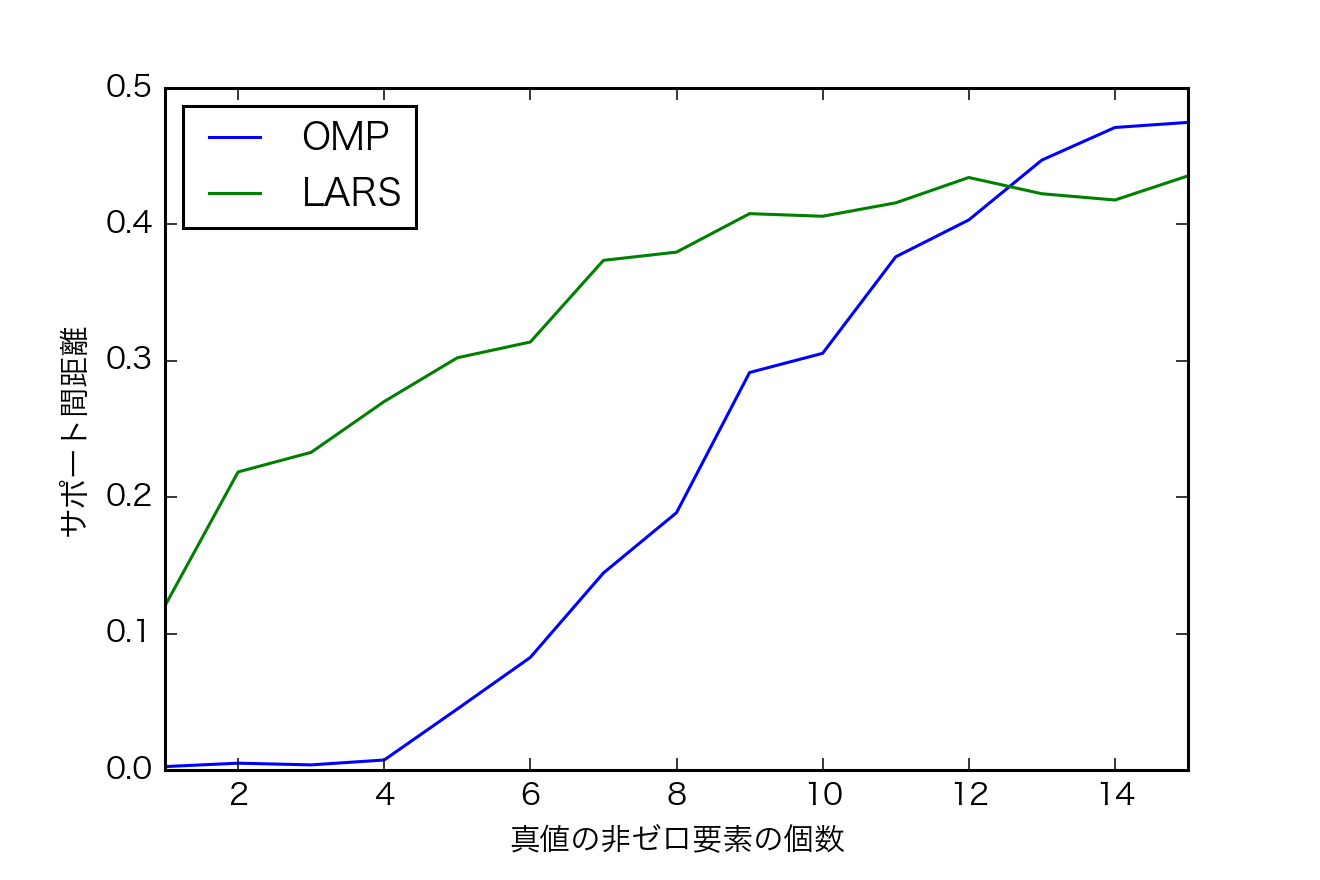
- $k=1,...,15$で各200回シミュレーション
- OMPとLARSを比較
指標
- 推定した$\mathbf{\hat{x}}$と真の$\mathbf{x}$の$L_2$ノルム
- 推定した$\mathbf{\hat{x}}$と真の$\mathbf{x}$のサポート間距離$$dist(\hat{S},S)=\frac{max\{|\hat{S}|, |S| \} - |\hat{S}\cap S|}{max\{|\hat{S}|,|S|\}}$$
- 200回のシミュレーションの平均をとる.
結果
考察
- kが小さい場合,OMPの方が誤差が小さい.kが大きい場合,LARSの方が誤差が小さい.
- サポートの復元はOMPの方が正確なよう.Kが大きくなると逆転する.