LoginSignup
437
376

More than 3 years have passed since last update.

@keymoon

【全方位木DP】明日使える便利な木構造のアルゴリズム

Last updated at Posted at 2020-03-28

この記事について

この記事では、一部で全方位木DP、Rerooting等と呼ばれているアルゴリズムの紹介/解説と、その実装についての簡単な説明を行います。
全方位木DPなどと物騒そうな名前がついていますが、発想自体は全く難しくありません。また、実装もそこまで難しいものではないです。
前提知識として、最低限のグラフ理論の知識(特に木構造について)を要求します。(有向木の根/部分木等…)

謝辞

この記事中に挿入されている図は、殆どを @259_Momone さんに提供して頂きました。素晴らしく美しい図を提供して頂き、この記事を分かりやすいものとして頂いたことに感謝いたします。

全方位木DPとは

各点から深さ優先探索を行って解くことができる問題のうち特定の条件(後述)を満たすものについて、全頂点についての答えを同等の計算量で求めることができるアルゴリズムです。

まず、全方位木DPで解くことができる簡単な例題を考えます。

問題
頂点が$N$個の木構造が与えられます。各頂点について、その頂点から最も遠い頂点の距離(通過する辺数)を求めてください。

例えば、図のような木構造を考えてみます。

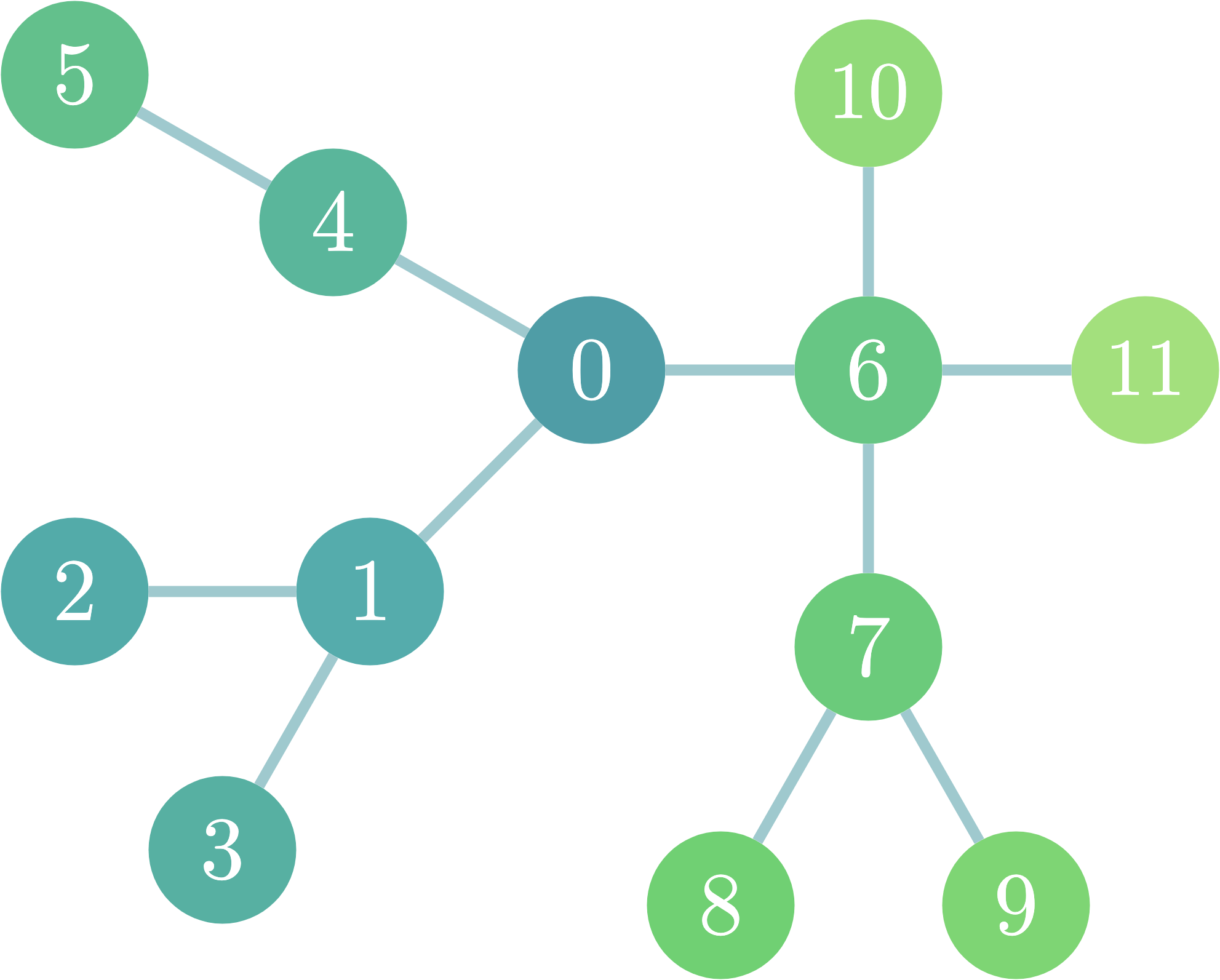
頂点8であれば頂点2,3,5が距離5なので5、頂点1であれば頂点8,9が距離4なので4となります。

この問題は各点から深さ優先探索等を行うことで解くことができますが、一度の探索で$N$頂点について探索することを各$N$点について行うため、計算量は$O(N^2)$となります。

深さ優先探索と部分木

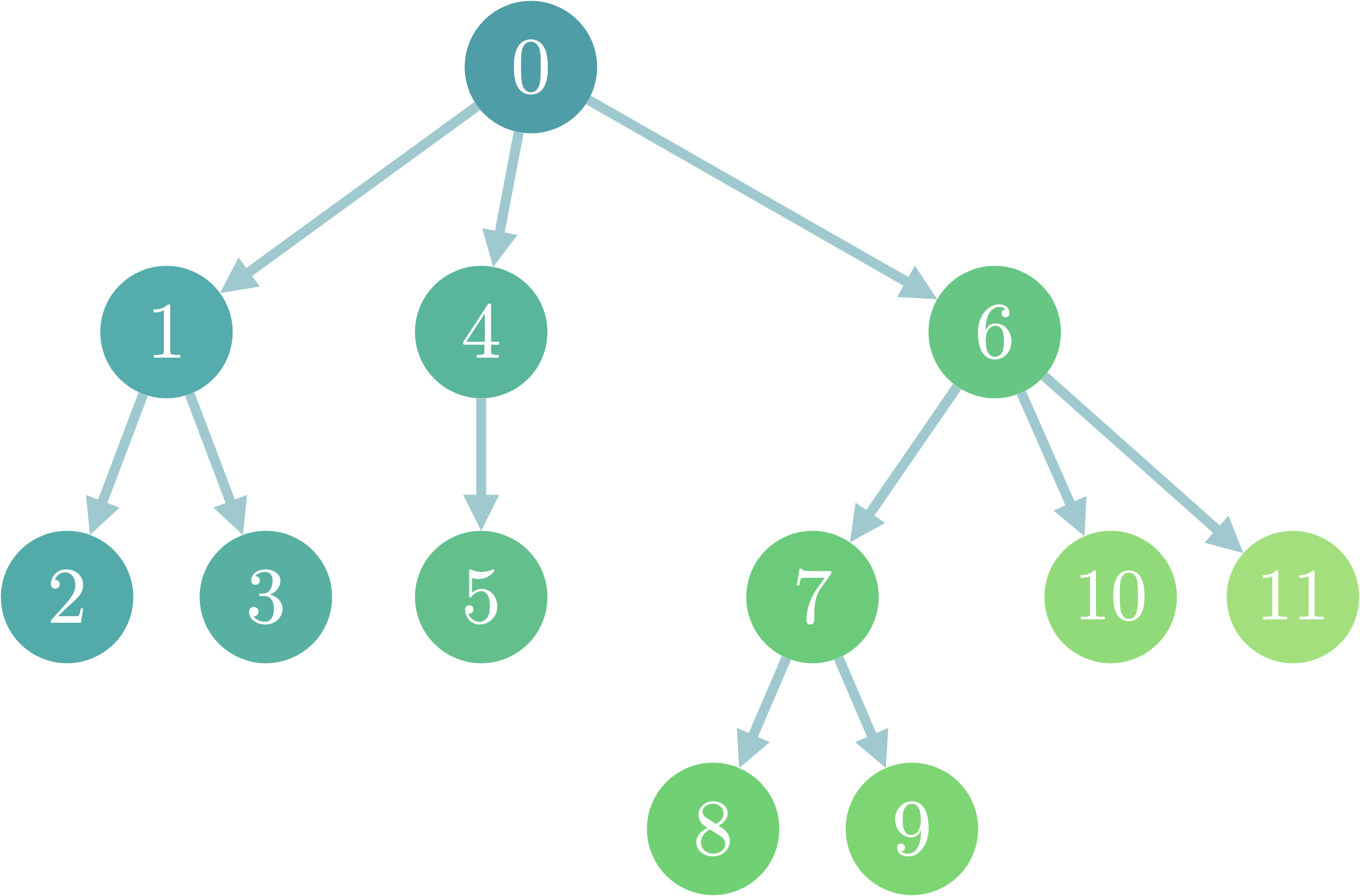
まず、愚直な$O(N^2)$解について考えてみましょう。この際、探索を開始する一点を根とした有向木として木を捉えると今後がわかりやすくなります。

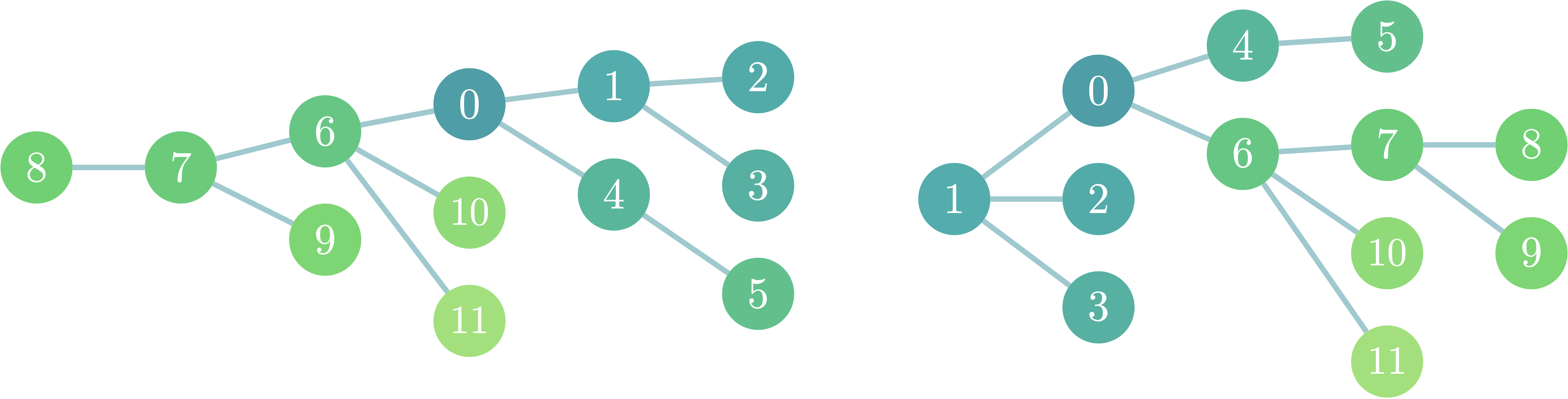
また、深さ優先探索を「木についての値を求める」ものと捉えた時、これは「自分の子が根となる部分木の値を求め、それらの結果をマージする」操作として捉えることができます(以下で解説します)。
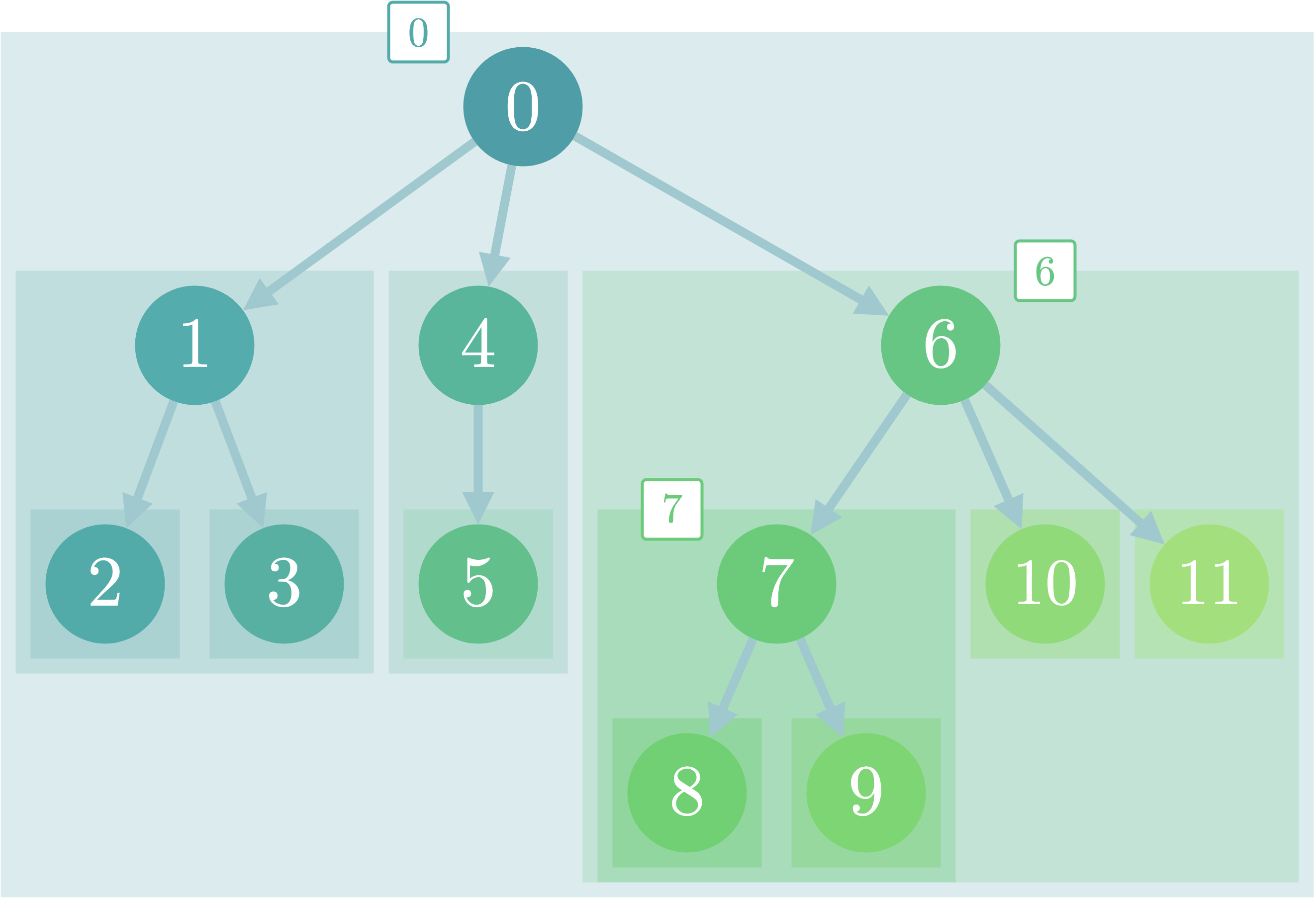
以下の図は部分木を□で表しています。それぞれの部分木は「自分の子を根とする部分木(以降子部分木と呼ぶ)」と「自分(根)」をマージしたものになっていることが分かると思います。(6を根とした部分木を考えた場合、「6の子部分木({7,10,11}を根とした部分木)」+「6」となります)

今回の問題では、それぞれの部分木について「部分木の根から最も遠い頂点への距離」という問題を解くことを考えます。これは全体の問題と同一ですね。部分木のマージにおいては、「子部分木の解のMaxに、根の深さ(1)を足す」という操作で解くことができます。それを実現するコードが以下です。

solve.cs
int N;
//adjacent[x] := xに隣接する頂点の集合
int[][] adjacents;
void Main()
{
    //全ての頂点についてDFS
    //親を存在しない値(-1)とすることは親が存在しないことを示し、DFS(i, -1)はiを根とした木構造でのDFSを表す
    for (int i = 0; i < N; i++) WriteLine(DFS(i, -1) - 1/*DFSの返り値は通過する頂点数なので、1引く*/);
}
int DFS(int root, int parent)
{
    int result = 0;
    //rootの全ての隣接する頂点に対して探索を行う
    foreach (var adjacent in adjacents[root])
    {
        //親方向には辺を伸ばさないようにする(根付き有向木を実現)
        if (adjacent == parent) continue;
        //子部分木についての答えと今までの答えをマージ
        result = Max(result, DFS(adjacent, root));
    }
    //自分のノードの分の深さを追加
    return result + 1;
}

以上の解法ですが、実は相当無駄があります。

結果のメモ化

例えば、DFS(6, 0)という関数は何度も呼び出されています。これは「頂点6を根、頂点0を親とした部分木」を示しています。

また、この関数の戻り値は常に一定です。なので、一度呼び出されたら次からはその値を再利用してあげれば良いということが分かります。
この場合、DFS関数が呼び出される回数は有り得る引数毎に一回ずつとなります。

solve.cs
int N;
//adjacents[x] := xに隣接する頂点
int[][] adjacents;
//memo[x][i] := DFS(adjacents[x][i], x)の値のメモ
int[][] memo;
//hasCalled[x][i] := DFS(adjacents[x][i], x) が呼ばれたことがあるか
bool[][] hasCalled;

void Main()
{
    for (int i = 0; i < N; i++) WriteLine(DFS(i, -1));
}
int DFS(int root, int parent)
{
    int result = 0;
    //rootの全ての隣接する頂点に対して探索を行う
    for (int i = 0; i < adjacents[root].Length; i++)
    {
        int adjacent = adjacents[root][i];
        //親方向には辺を伸ばさないようにする
        if (adjacent == parent) continue;
        //もしまだ呼ばれたことがなければメモする
        if (!hasCalled[root][i])
        {
            memo[root][i] = DFS(adjacent, root);
            hasCalled[root][i] = true;
        }
        //メモと今までの結果をマージ
        result = Max(result,  memo[root][i]);
    }
    //自分の深さを追加
    return result + 1;
}

このコードは一見高速に動作するように思えます。DFSが呼ばれる回数は$3N$回程度1と呼び出し回数は改善されています。
しかし、隣接頂点数が多い頂点が存在していたらどうなるでしょうか。以下のようなスターグラフと呼ばれるグラフの場合を考えてみましょう。

頂点数を$N$、中央の頂点を$0$としたとき、頂点$0$に隣接する頂点数は$n-1$個です。よって、どの頂点を根としても、頂点$0$の子部分木の個数は$N-2$個存在します。

頂点$0$を親とする部分木の値を求めるためには隣接するすべての頂点について調べる必要があるため、DFS(0, n)を求めるためには$N-2$回以上ループを回さなければいけません。
頂点$0$を根とする部分木の種類は隣接する頂点数だけあるため、$n-1$種類となります。

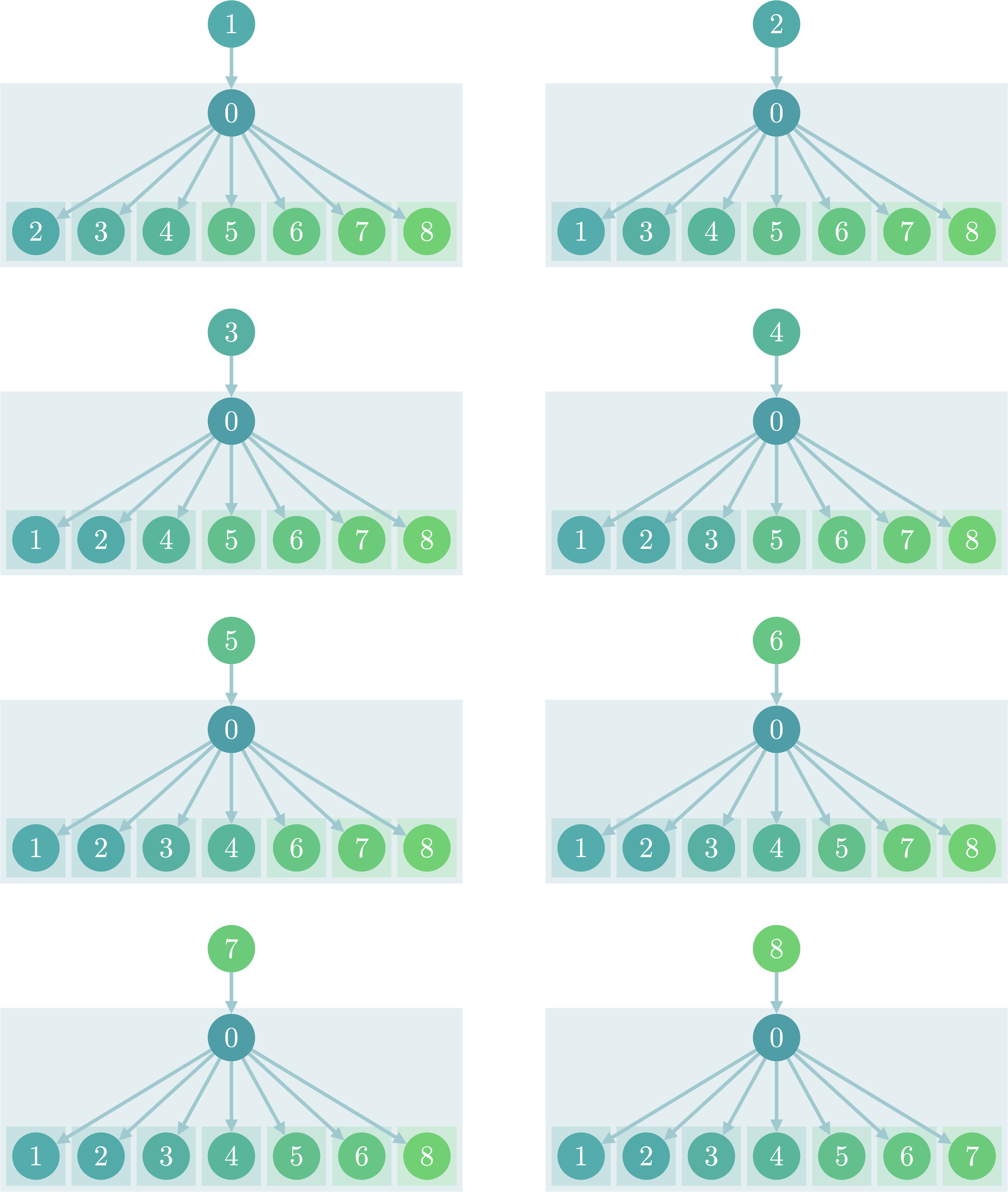
このそれぞれの部分木について$O(N)$の計算量がかかるため、結果として最悪ケースについては$O(N^2)$の計算量がかかることになってしまいます。

結果の一括計算

ここで、「自分を根とするありうる全ての部分木」の値を一括で計算してみることについて考えることにします。

これらの情報は共通部分が大きいため、何らかの方法で計算結果を再利用できそうです。
まず、DFS(0, 8)(0を根とし、8を親とする部分木についてのDFS)を呼ぶ際に得られる情報について考えてみます。

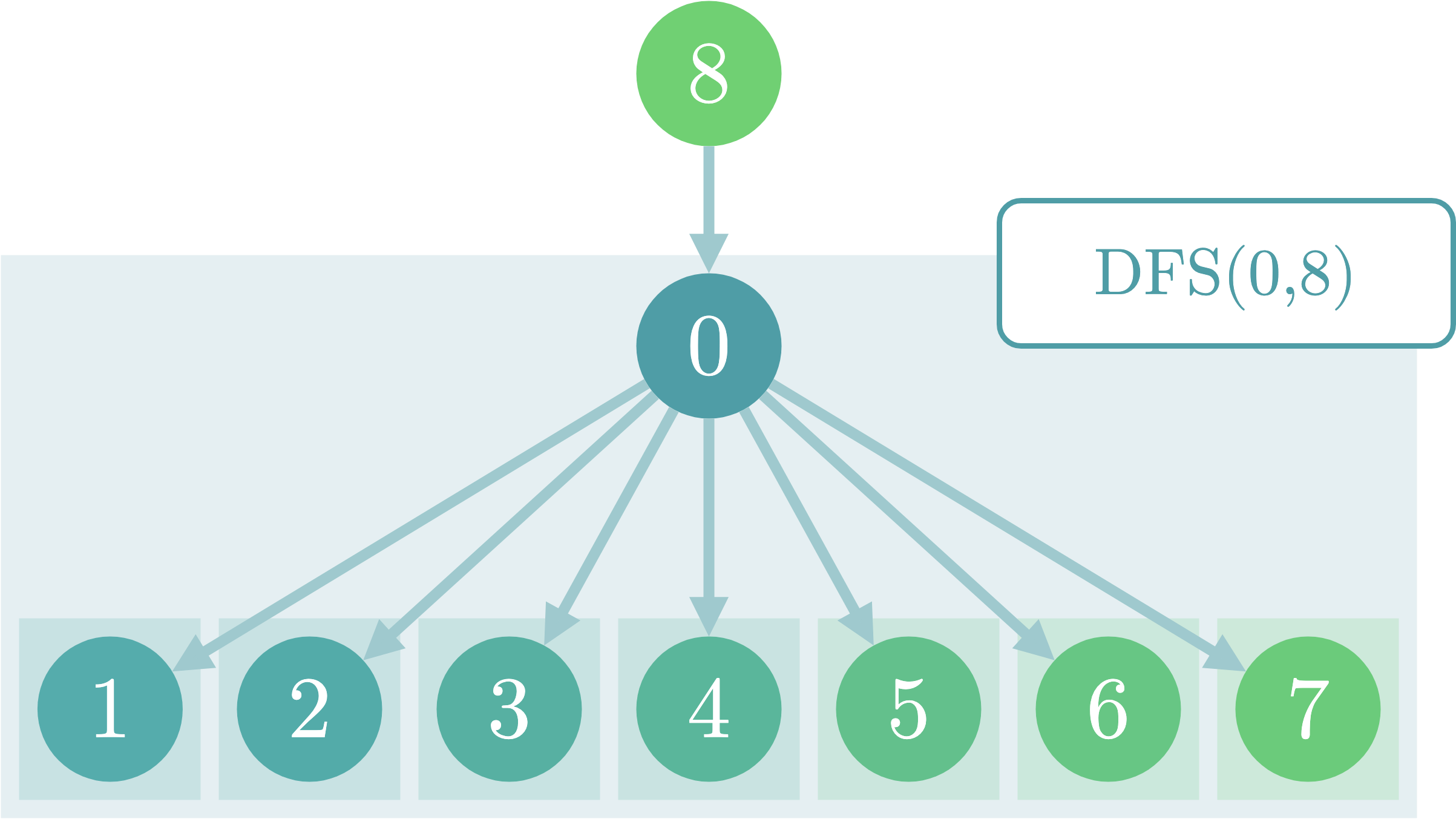
もちろん子部分木の値をマージした値は得られますが、本当に得られる情報はこれだけでしょうか?
子部分木をマージする過程をもう少し細かく見ていくことにします。resultに作用するところだけ取り出してみると、以下のコードのようになります。

int result = 0;
result = Max(result, memo[root][0]);
result = Max(result, memo[root][1]);
result = Max(result, memo[root][2]);
result = Max(result, memo[root][3]);
result = Max(result, memo[root][4]);
result = Max(result, memo[root][5]);
result = Max(result, memo[root][6]);

これは、memo[root][0]からmemo[root][6]までの累積Maxを順々に求めていっていることに他なりません。図にすると以下のようになります。

ここで、逆からの累積Maxも考えてみます。
このようにすると、DFS関数の取りうる全ての値を2つの累積MaxのMaxで表せることが分かります。

より形式的に書くと、「『子部分木の値の左から/右からの累積Max』を計算した上で、全ての親方向において該当する累積Maxをマージすれば良い」となります。
累積Maxと全地点でのマージの回数はありうる親の数、つまり隣接する頂点数=辺の数に比例します。
辺の総数は$N-1$本で、全ての辺は両端の2回から見られるため、全頂点での隣接する頂点数は$2(N-1)\in O(N)$個となります。
よって、累積Max,マージの回数を$O(N)$で抑えながら全頂点についての値を求めることができました。

一般にどのような操作が可能か

今回扱ったint内でのMaxのように、

  • 同じ型の要素を2つとり、1つの同じ型の要素を返す
  • 操作をfとしたときに、f(a, f(b, c))=f(f(a, b), c))が成立する(演算の順序を入れ替えても結果が変わらない。結合法則が成立する)
  • どんな値aについてもf(a, id)=aかつf(id, a)=aが成立するidが存在する。(単位元idの存在)

が成り立つ操作をモノイドと呼びます。2

たとえば、int内でのMaxは

  • intとintをとってintを返す
  • Max(a, Max(b, c))=Max(Max(a, b), c)=Max({a, b, c})なので、結合法則が成立
  • Max(-inf, a)=Max(a, -inf)=aなので、-infが単位元

となるため、これはモノイドをなすことが分かります。

他にも、足し算や掛け算、0を単位元としたGCD等はモノイドをなします。
全方位木DPでは累積和によって前計算したものをマージするため、演算順序がバラバラになるので結合法則が必須になります。また、累積和の開始に単位元を置きたいため、単位元の存在を条件とすることにします3。よって、全方位木DPが可能な操作はモノイドである必要があることが分かります。

補足:もうひとつの全方位木DP

今回はモノイドの場合でしたが、以下のような条件を満たす場合はもう少し単純に書くことができます。
操作をfとした時に、

  • fがモノイドをなす
  • idを単位元とした時に、ある値aについてf(a,inv)=idを満たすようなinvが全ての値について存在する(逆元の存在・可逆性)
  • f(a,b)=f(b,a)が成立する(交換法則の成立・可換性)

が成立すれば良いです。このような演算を可換群と呼びます。4

例えば、整数での+は、

  • モノイドをなす(結合法則は成立し、0が単位元)
  • a+(-a)=0なので、任意のnについて-nが逆元
  • a+b=b+aなので、交換法則が成立

なので可換群です。

他にも、0を除いた実数上や素数Mod上での乗算や、ビット列のxorも可換群をなします。

この場合、DFS(a,b)(aを根としたbが親の部分木の値)はDFS(a,-1)(aを根とした木の値)とDFS(b,a)(bを根としたaが親の部分木の値)を用いてf(DFS(a,-1),inv(DFS(b,a)))と計算できます。
DFS(a,-1)(aを根とした木の値)が求まっているということは、aの全ての子部分木の値(DFS(n,a),nは任意のaに隣接する点)が求まっているということなので、上記の計算はDFS(a,-1)が求まっているならば可能であることが分かります。

上で述べた手順は特定のケースにおいての実装の簡略化や高速化について使うことができ、このような手順を取ることができるのであれば、両方向累積を用いた実装も可能です。

実装

上で見てきたように、全方位木DPはマージがモノイドである時に行うことができます。逆に言えば、「全方位木DPはモノイドとなる演算すべてを扱うことができる」ということです。
そのため、使用時にターゲットとなる木構造とモノイドの演算と単位元、頂点を木構造に追加する際の演算のみを与えれば良いような、柔軟な実装5を本記事では行うことにします。

与えられる情報

全方位木DPを行う関数/クラスには、以下の引数を与えることにします。

//ノードの数
int nodeCount;
//{{0,1},{0,2},{1,2}}のような木構造の辺の配列
int[][] edges;
//単位元
T identity;
//T merge(T left, T right) { } で定義される部分木のマージ関数
Func<T, T, T> merge;
//T addNode(T value, int nodeID) { } で定義される頂点の追加関数
Func<T, int, T> addNode;

Step.0 木構造の情報を記録する

この先実装していくにあたって、
・隣接している点の配列
・隣接点にとって自分が何番目の隣接点なのか
が必要です。なので、それらを先に記録しておきます。

実装
//隣接頂点,隣接頂点から見た自分のindex を保持するリストの配列を作成
//adjacents[i] := 隣接している頂点の配列
List<int>[] adjacents = Enumerable.Repeat(0, nodeCount).Select(_ => new List<int>()).ToArray();
//indexForAdjacents[i][j] := adjacents[i][j](iのj番目の隣接頂点)にとって、iが何番目の隣接頂点か
//                           つまり、 adjacents[adjacents[i][j]][indexForAdjacents[i][j]] == i である
List<int>[] indexForAdjacents = Enumerable.Repeat(0, nodeCount).Select(_ => new List<int>()).ToArray();

//辺を見て配列に追加していく
foreach (int[] edge in edges)
{
    indexForAdjacents[edge[0]].Add(adjacents[edge[1]].Count);
    indexForAdjacents[edge[1]].Add(adjacents[edge[0]].Count);
    adjacents[edge[0]].Add(edge[1]);
    adjacents[edge[1]].Add(edge[0]);
}

//childSubtreeRes[i] := iの子部分木の値
//childSubtreeRes[i][j] := iを親とし、adjacents[i][j]を根とした部分木の値  
T[][] childSubtreeRes = Enumerable.Range(0, nodeCount).Select(i => new T[adjacents[i].Count]).ToArray();
//nodeRes[i] := iを根としたときの結果結果
T[] nodeRes = new T[adjacents.Length];

Step.1 一つの頂点について求められるようにする

まず、一つの頂点について求めることを考えます。そのため、一時的に求めたい頂点を根とした根付き木を考えます。
この時、初期状態の何も値が求まっていない状態で値を求められる部分木は、葉のノード一つだけの部分木のみであることが分かります。また、子の値が全て求まった頂点については、その値も求められます。
そのため、「子を全て探索しないと親を探索できない」というルールに則った順序で求解していけば良いです。
これは、「まず親を探索しなければその子を探索できない」というルールの逆になっているため、そのようなルールで行った探索の逆順が該当します。
よって、DFSやBFS等をした順序の逆、一般には帰りがけ順やレベル順等として知られている順序で訪問すれば良いです。今回はDFSの順序の逆、帰りがけ順を採用することにします。

後からも使うので、DFSでの訪問順、行きがけ順を配列に記録します。
実装では、行きがけ順を記録すると同時に各頂点についての親を記録しておくと便利です。

実装
//parents[i] := 一時的な根付き木として考えた時の、ノードiについての親
int[] parents = new int[NodeCount];
//order := DFSでの行きがけ順
int[] order = new int[NodeCount];

var index = 0;
Stack<int> stack = new Stack<int>();
//0を根とする
stack.Push(0);
parents[0] = -1;
//行きがけ順を記録する
while (stack.Count > 0)
{
    var node = stack.Pop();
    order[index++] = node;
    for (int i = 0; i < adjacents[node].Length; i++)
    {
        var adjacent = adjacents[node][i];
        if (adjacent == parents[node]) continue;
        stack.Push(adjacent);
        parents[adjacent] = node;
    }
}

その次に、その訪問順を利用して部分木の値を求めます。今の部分木の親が持っている配列に今の結果、つまり親から見た子部分木の値を格納するためには、先程作った隣接点にとって自分が何番目の隣接点なのかを格納した配列を使うと便利です。

実装
//帰りがけ順で部分木の値を求めていく
for (int i = order.Length - 1; i >= 1; i--)
{
    //現在の見ている頂点と、その親
    var node = order[i];
    var parent = parents[node];
    //結果
    T result = Identity;
    int parentIndex = -1;
    //隣接する点を調べる
    for (int j = 0; j < adjacents[node].Length; j++)
    {
        //もし隣接する点が親だったら、親のindexの記録だけする
        if (adjacents[node][j] == parent) { parentIndex = j; continue; }
        //隣接する点方向の子部分木の結果を加える
        result = merge(result, childSubtreeRes[node][j]);
    }
    //頂点を部分木に追加した後、親が持っている配列に結果を格納する(親にとって自分が何番目の隣接頂点なのかを調べて格納)
    childSubtreeRes[parent][indexForAdjacents[node][parentIndex]] = addNode(result, node);
}

Step.2 全ての頂点の値について求める

上の操作によって、根付き木の根の方向(=親方向)以外の部分木の値が求まっているような状態になります。よって、全ての頂点は根の方向からの部分木の値が求まれば頂点の値が求まるという状態になっています。
先程も述べたように、子部分木全てが揃った場合、両方向から累積を取る等で自分が根となる全ての部分木の値を求めることができます。
今、各頂点が欲しいものは親が根の部分木の情報なので、ある頂点の値が求まったら、その頂点が親の頂点(=子)の値を求めることができるようになることが分かります。
よって、「親を確定させてからその子を確定させていく」という順序で確定させていけば良いです。
これは、DFSやBFS等をした順序、一般には行きがけ順等として知られている順序で訪問すれば良いです。
先程行きがけ順を前計算したものがあるため、それを活用して実装をします。

実装
//行きがけ順で頂点の値を確定させていく
for (int i = 0; i < order.Length; i++)
{
    //値を確定させるnode
    var node = order[i];
    //後ろからの累積和を格納する配列
    T[] accumsFromTail = new T[adjacents[node].Count];
    accumsFromTail[accumsFromTail.Length - 1] = identity;
    for (int j = accumsFromTail.Length - 1; j >= 1; j--) accumsFromTail[j - 1] = merge(childSubtreeRes[node][j], accumsFromTail[j]);
    //前からの累積和を持つ変数
    T accum = identity;
    for (int j = 0; j < accumsFromTail.Length; j++)
    {
        //adjacents[node][j]が親、nodeが子の部分木について計算する
        //累積をマージして子部分木の値をマージし終えた後、頂点を追加する
        T result = addNode(merge(accum, accumsFromTail[j]), node);
        //その値を、親が持っている配列に結果を格納する(親にとって自分が何番目の隣接頂点なのかを調べて格納)
        childSubtreeRes[adjacents[node][j]][indexForAdjacents[node][j]] = result;
        //累積を更新
        accum = merge(accum, childSubtreeRes[node][j]);
    }
    //最後まで累積しきったものはnodeの子部分木を全てマージしたものになっているので、それに頂点を追加するとnodeの値となる
    nodeRes[node] = addNode(accum, node);
}

まとまった実装は以下になります。(各言語での実装、募集しています!)
実装(C#)
実装(C++) by @noshi91
実装(Ruby) by @obelisk68
実装(Rust) by @vain0x
実装(Go) by @_maguroguma

以上の手順をアニメーションにすると、以下のようになります。
小さな赤丸はその方向の子部分木の値が確定していることを示し、大きな赤丸はその頂点の値が確定したことを示します。
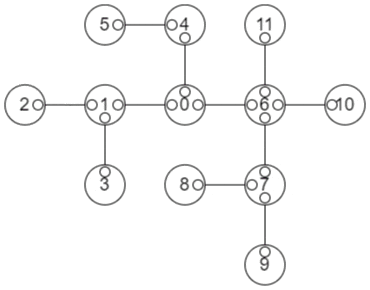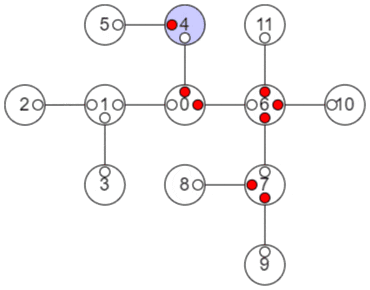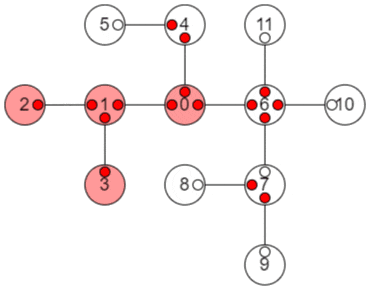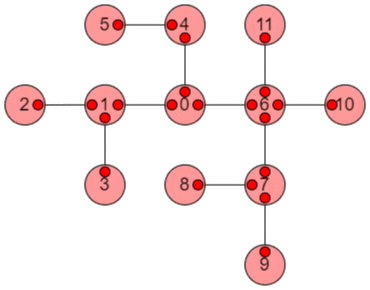
res.gif

使用例

以上の全方位木DPを実装して、nodeResの配列を返す関数をReRootingとします。

T[] ReRooting<T>(int nodeCount, int[][] edges, T identity, Func<T, T, T> merge, Func<T, int, T> addNode) { /*実装略*/ }

これを用いて、最初の問題を解いてみます。(以下に再掲)

問題
頂点が$N$個の木構造が与えられる。各頂点について、その頂点から最も遠い頂点の距離(通過する辺数)を求めよ。

これの実装は、以下のようになります。

int nodeCount;
int[][] edges;

int[] res = ReRooting<int>(nodeCount, edges, 0, Max, (value, id) => value + 1);
foreach (int item in res) Console.WriteLine(item - 1);

addNode関数は、最初の実装の

int DFS(int root, int parent)
{
    int result = 0;
    //rootの全ての隣接する頂点に対して探索を行う
    foreach (var adjacent in adjacents[root])
    {
        //親方向には辺を伸ばさないようにする(根付き有向木を実現)
        if (adjacent == parent) continue;
        //子部分木についての答えと今までの答えをマージ
        result = Max(result, DFS(adjacent, root));
    }
    //自分のノードの分の深さを追加
    return result + 1;
}

のreturn result + 1にあたるところです。

では、もう少し難しい問題を解いてみましょう。(この先は実際にEducational DP Contestに出た問題を解いてみます。ネタバレが嫌な人は見ないほうがいいかも)

問題
頂点が$N$個の木構造が与えられる。各頂点を白または黒で塗る彩色のうち、どの黒い頂点からどの黒い頂点へも、黒い頂点のみを辿って到達できるような彩色を考える。頂点$v$が黒であるような彩色は何通りか。$\bmod m$で求めよ。
出典 : EDPC-v

まず、一つの頂点について求めることを考えます。ある頂点について、もし全ての子部分木が「根から全ての黒の頂点に到達可能である」ならば、親の頂点を黒く塗った時にも同様の条件を満たすようになることがわかります。
なので、ある部分木についての結果は、「(全ての子部分木の結果を掛け合わせたもの)+1」になることが分かります。+1する理由としては、上の条件を満たす彩色として「全て白」というものがあり、この場合だとそれを網羅することができないからです。また、子部分木をマージする演算は乗算であり、この演算は可換的であることが分かります。
よって、この問題は全方位木DPで解くことができます。

コードは以下の通りです。出力に際し、「全て白」というものを追加した結果を除きたいために-1しています。

int nodeCount;
int[][] edges;

long[] res = ReRooting<long>(nodeCount, edges, 1, (x, y) => (x * y) % m, (value, id) => value + 1);
foreach (long item in res) Console.WriteLine(item - 1);

この問題は、逆元が存在しない場合の全方位木DPの例題にもなっています。(modが任意で指定されるため、そのmodが素数であるとは限らない。)

  1. 厳密には$3N-2$(adjacentsの各要素数の合計+N)です。memoをするための呼び出しが要素数の合計回、最初に呼ばれるDFS(i, -1)がN回です。adjacentsの要素は辺の両端にあるため辺の数*2であることが分かり、これは$2(N-1)$だからです。 ↩

  2. 一般に、(集合S, Sの元を取る演算, 単位元)という組をモノイドとすることが多いです。しかし、ここでは簡略化のために操作をモノイドとして扱っています(こう扱うことによって厳密性もそこまで損なわれないと考えました。) ↩

  3. 単位元の存在については、仮定すると実装が楽になるため仮定しています。単位元が必要なく、結合法則のみ成立するものを半群と呼び、実はこれでも実装は可能です。しかし、半群はある元を付加して単位元とすることでモノイドにすることが可能なため、競技プログラミングの範囲内ではモノイドが条件と言って良いでしょう。(細かい場合分けも実質的には単位元の付加をしているようなものです。) ↩

  4. 可換性を仮定しない場合、群と呼びます ↩

  5. これが抽象化と呼ばれているものです。 ↩

437
376
6

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
437
376