「データ解析のための統計モデリング入門」(通称:みどりぼん)のp157 にある、「分布を混ぜる」の考え方について、分布で考えるのではなく乱数ベースでシミュレーションを行いアニメーションで可視化をしてみましたので紹介したいと思います。
結果のアニメーションはこちらです。本文でこの内容を説明していきます。
(コードはこちら)
詳細な説明はこの「みどりぼん」に全てわかりやすく書いてあるので、ここでは可視化するにあたっての解説のみを行います。なんだか面白そうな話だと思いましたら是非ご購入ください!
前置き
ある植物において種子が最大8個作られるのですが、その種子の生存個数が二項分布、
p(y_i) ={8 \choose y_i}\ q_i^{y_i} (1-q_i)^{8-y_i} \quad \mbox{for}\ q_i=0,1,2,\dots,8
に従っているとします。$y_i$は個体$i$の生存種子数(観測値)、$q_i$は個体$i$における種子1つあたりの生存確率とします。
また、この$q_i$が個体によって異なる個体差を持ち、ロジスティック関数で表されるとします。
q_i = {\rm logistic} (r_i)= {1 \over 1 + \exp( -r_i) }
また、このロジスティック関数の引数$r_i$は、平均0, 標準偏差$s$の正規分布に従うと仮定します。
r_i \sim N(0, s)
つまり、$r_i$の密度関数は
p(r_i | s) = {1 \over \sqrt{2\pi s^2} } \exp \left( -{r_i^2 \over 2s^2} \right)
となり、これを個体$i$の個体差とみなします。
可視化してみる。
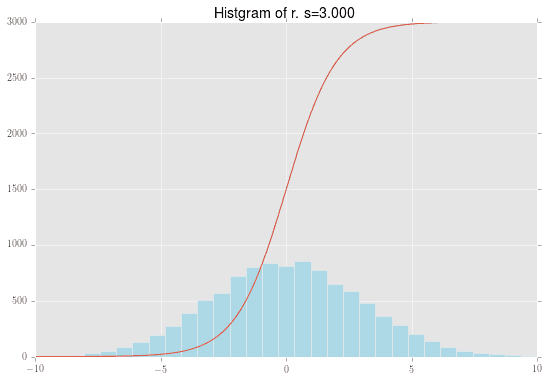
さて、まず個体差 $r_i\sim N(0, s)$を図示します。標準偏差 $s=4$の時の正規分布に従う乱数を10000個生成しました。そのヒストグラムが下記の水色の棒です。この一つ一つが赤い線で表されるロジスティック関数
q_i = {\rm logistic} (r_i)= {1 \over 1 + \exp( -r_i) }
で0から1の値、つまり確率と見なせる値、つまり$q_i$に変換されます。
この正規乱数一つ一つが確率$q_i$に変換できたので、それを$q_i$のヒストグラムとして表現したものが下記になります。割と幅広の正規分布であり、それをロジスティック関数で変換した影響で、0と1に寄っていることがわかります。
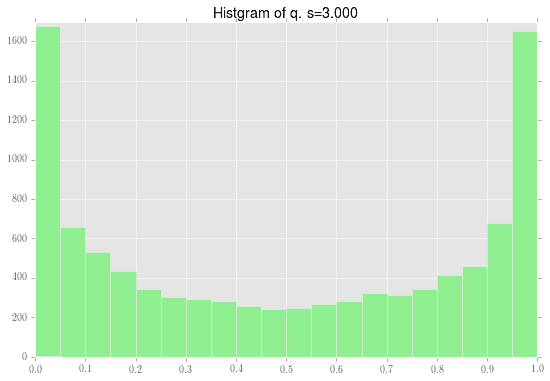
で、この10000個の$q_i$一つ一つに対して、二項分布を対応させます。
二項分布は、
p(y_i) ={8 \choose y_i}\ q_i^{y_i} (1-q_i)^{8-y_i} \quad \mbox{for}\ q_i=0,1,2,\dots,8
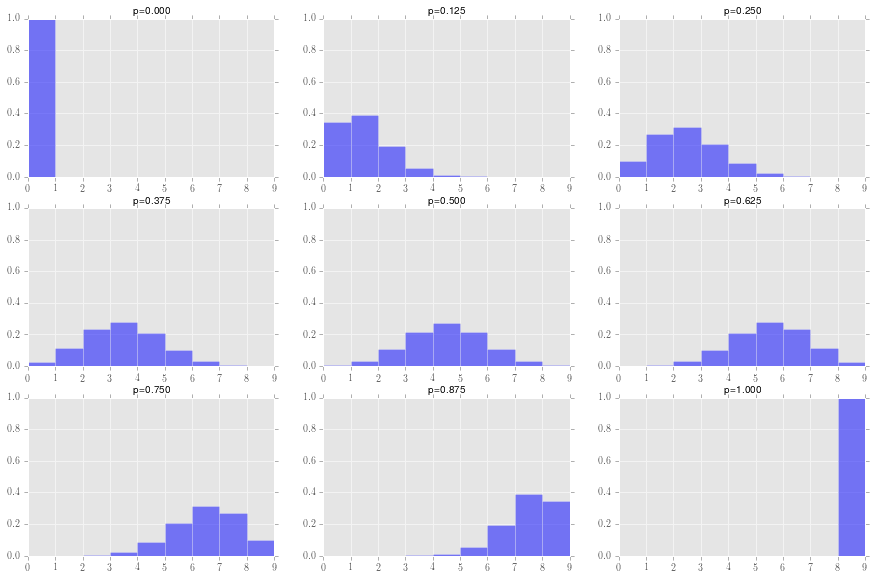
なので、$q_i$ごとに形状が異なります $q_i$が[0.0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1.0]の9つの値の例を下記に記します。
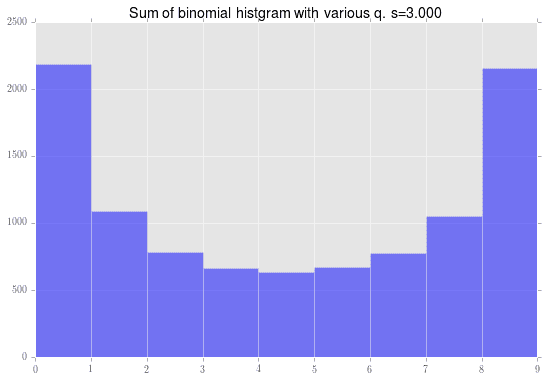
10000個の$q_i$の値に応じて上記のように多数の二項分布を生成しそれを足し合わせます。
足し合わせた結果がこちらです。
アニメーションしてみる
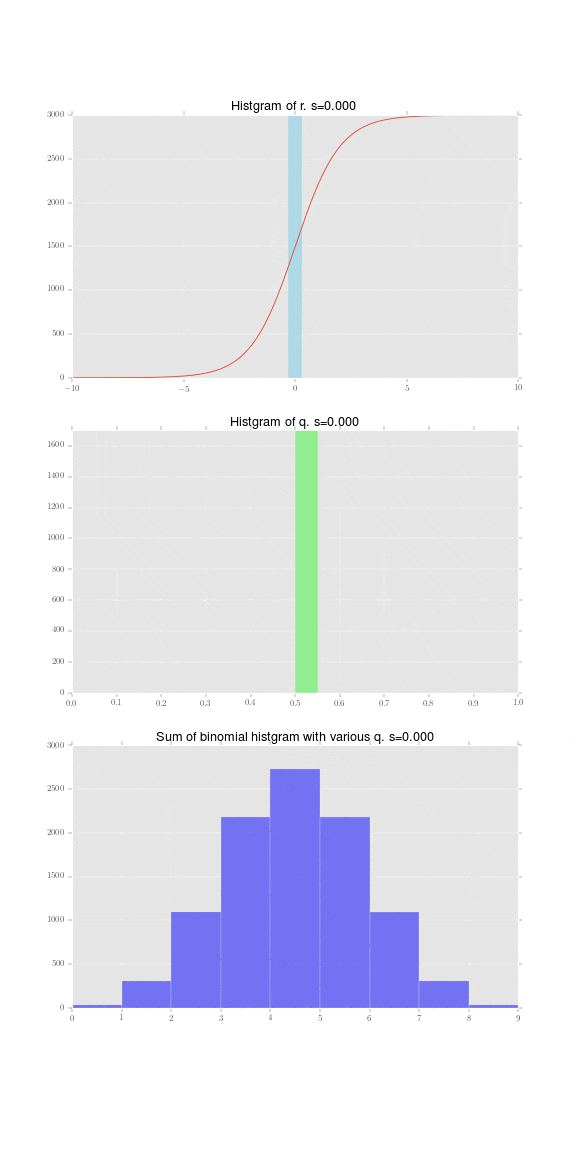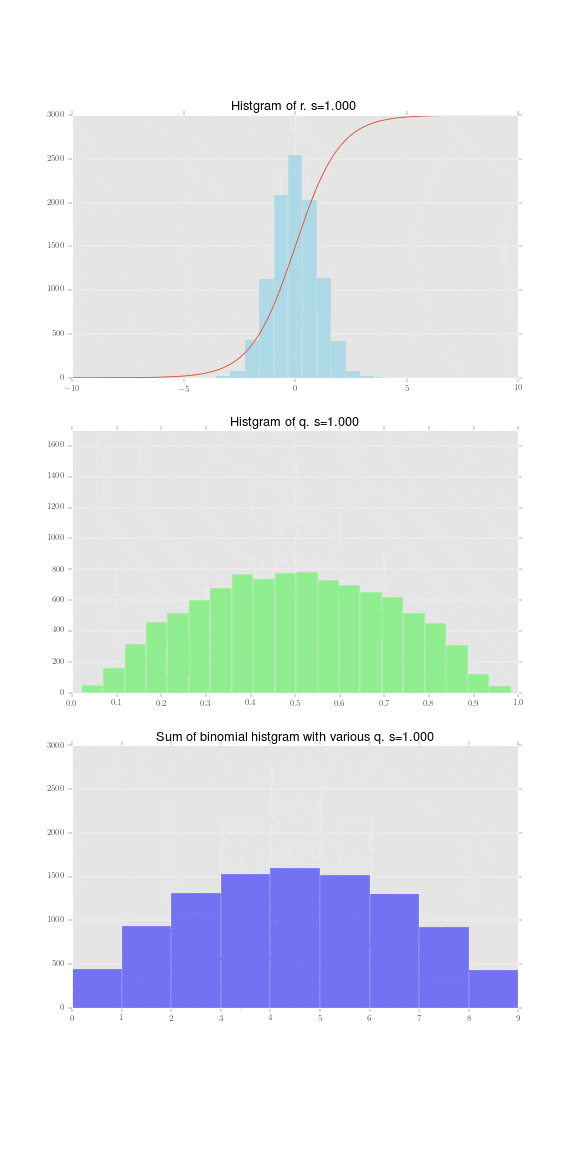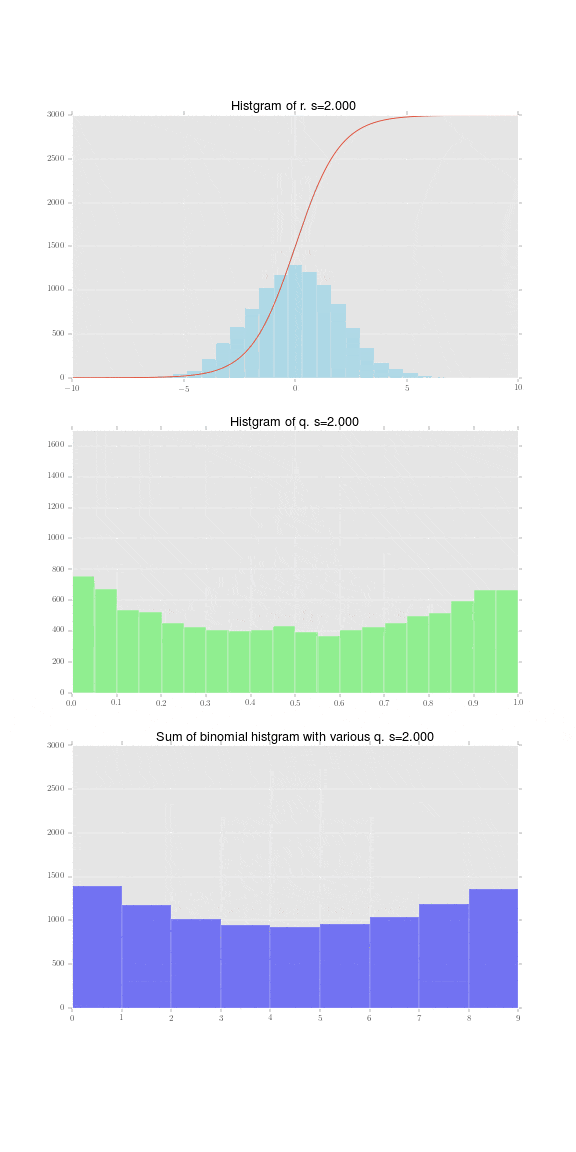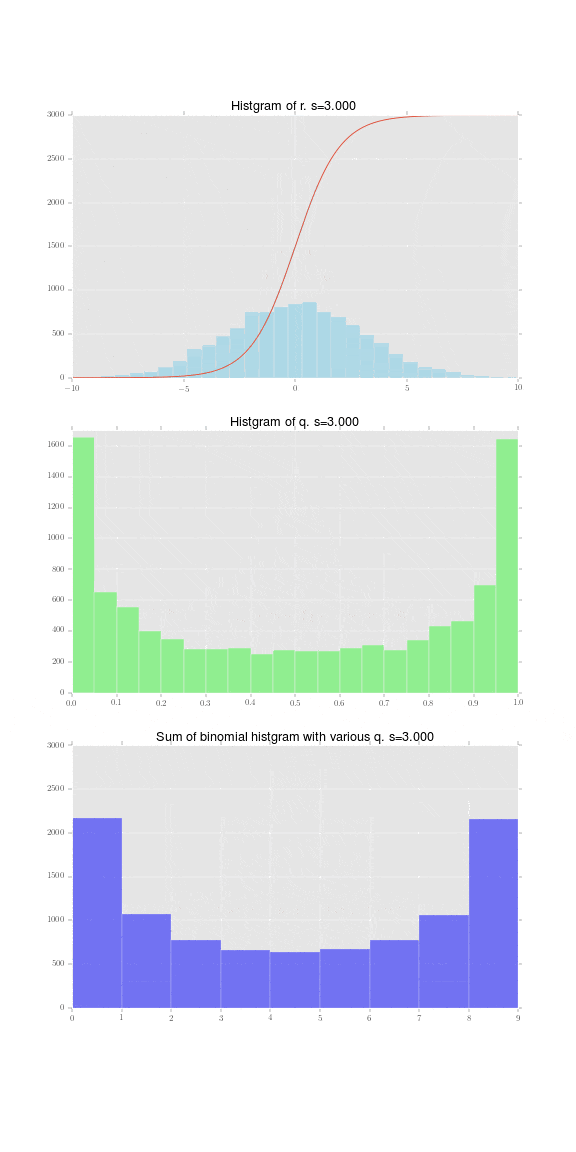
前項では $s=4$の例をグラフにしてみましたが、$s$が0から3まで連続的に動いた時の様子をアニメーションにしたのが冒頭にも掲載しました下記のグラフになります。
この例では、$s=2$前後から分布が左右に寄ってしまうようです。
参考書籍
データ解析のための統計モデリング入門
http://hosho.ees.hokudai.ac.jp/%7Ekubo/ce/IwanamiBook.html