ARMAモデルをひたすらプロットしてみる記事です。
${\rm ARMA}(p,q)$のパラメータによってどのようにグラフが変化するかを視覚的に理解するためにグラフを描きまくります。計49本ありますw ずっと眺めていたら、グラフを見てパラメーターが見分けられるようにならないかなー、という淡い期待から書いてみた記事です ![]()
グラフを並べて眺めた後、これらを生成したPythonコードを記載します。
自己回帰移動平均(ARMA)モデル
ARMAモデルの式は下記になります。本記事では $p=0,1,2,\ q=0,1,2$のパターンで、かつ各パラメータの符号のバリエーションの数だけグラフを描いていきます。
y_t = \varepsilon_t + \sum_{i=1}^p \phi_i y_{t-i} + \sum_{i=1}^q \theta_i \varepsilon_{t-i} \\
\varepsilon_t \sim N(0,\sigma^2) \\
t = 1, 2, \cdots, T
グラフを描画する
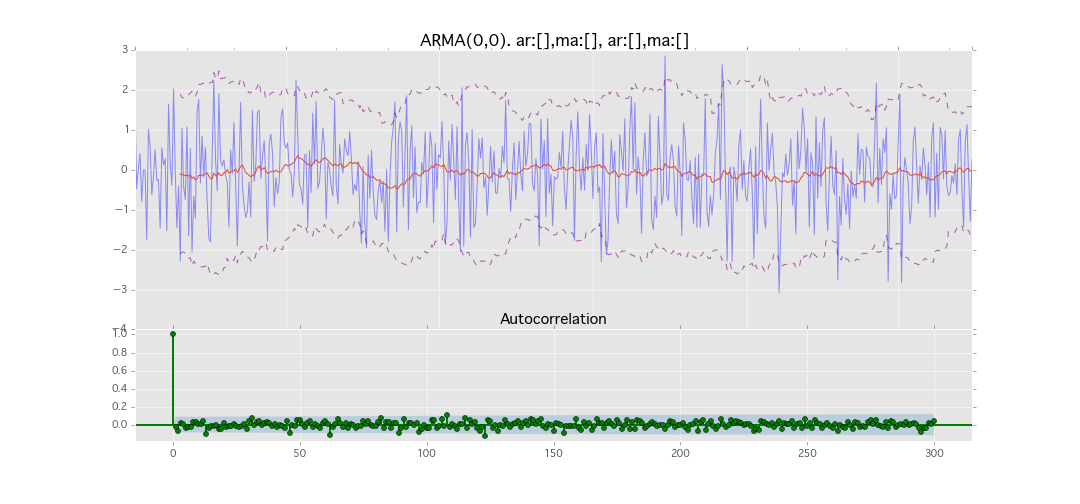
ARMA(0,0)
y_t = \varepsilon_t
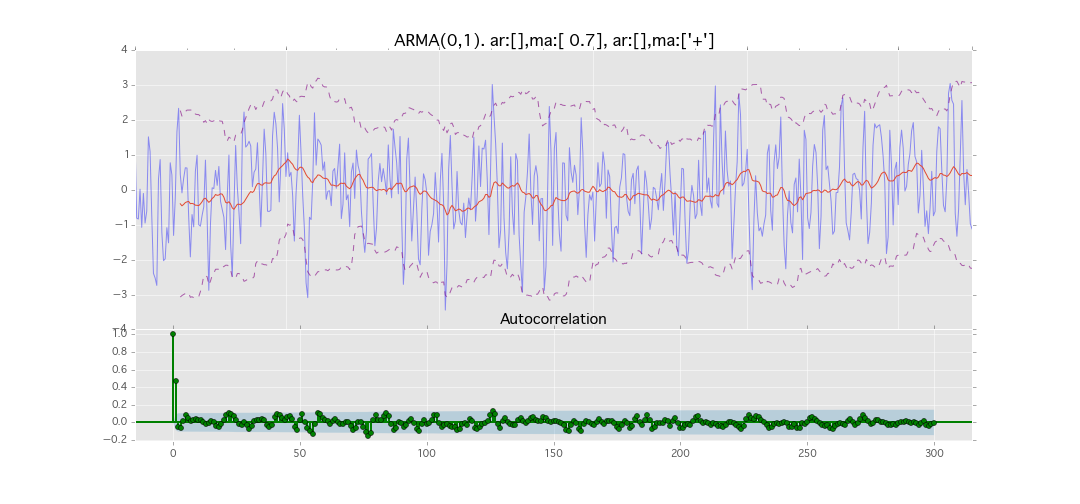
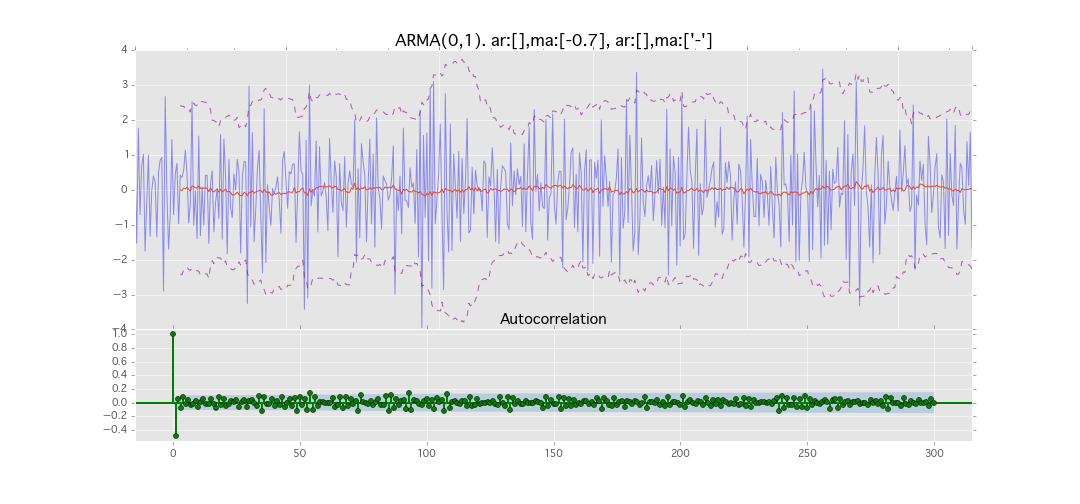
ARMA(0,1)
y_t = \varepsilon_t + \theta_1 \varepsilon_{t-1}
パラメータ:
$\theta_1=0.7$
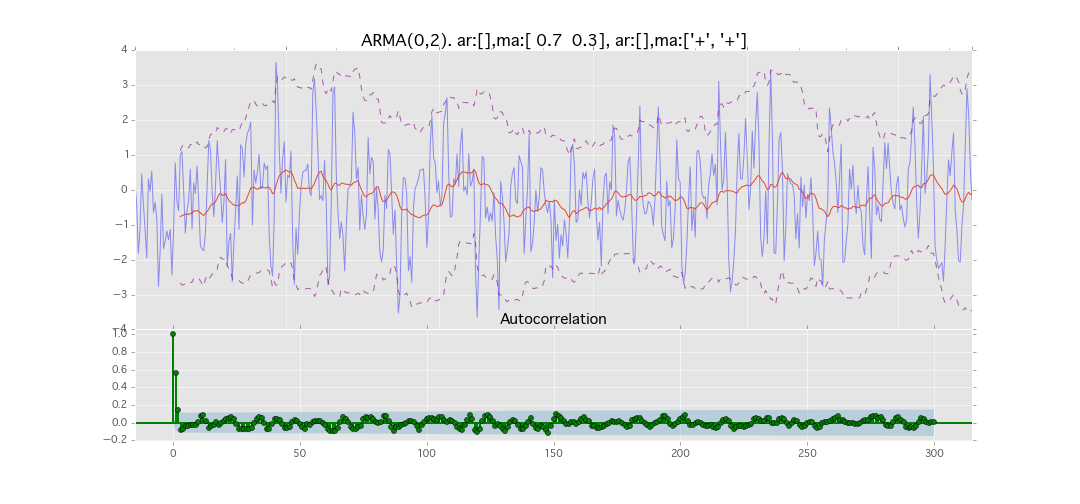
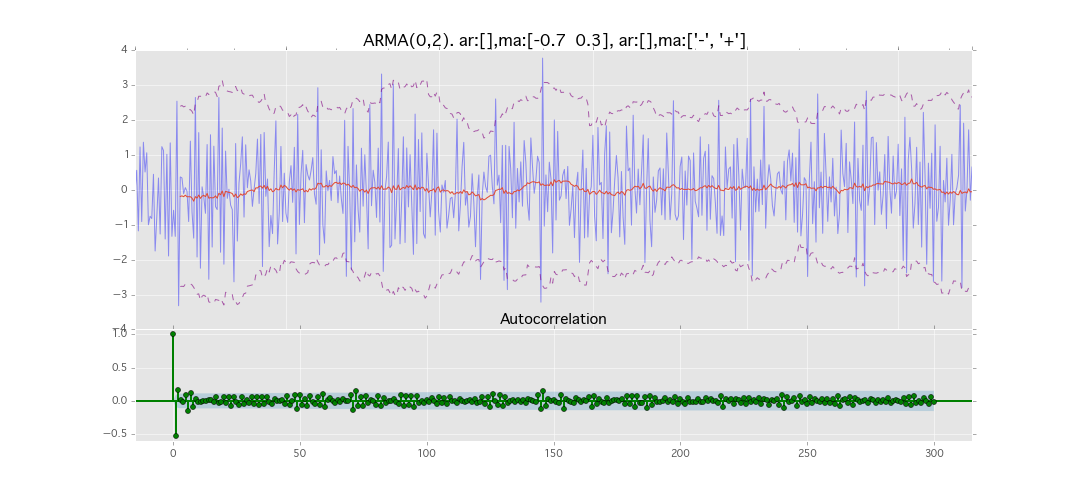
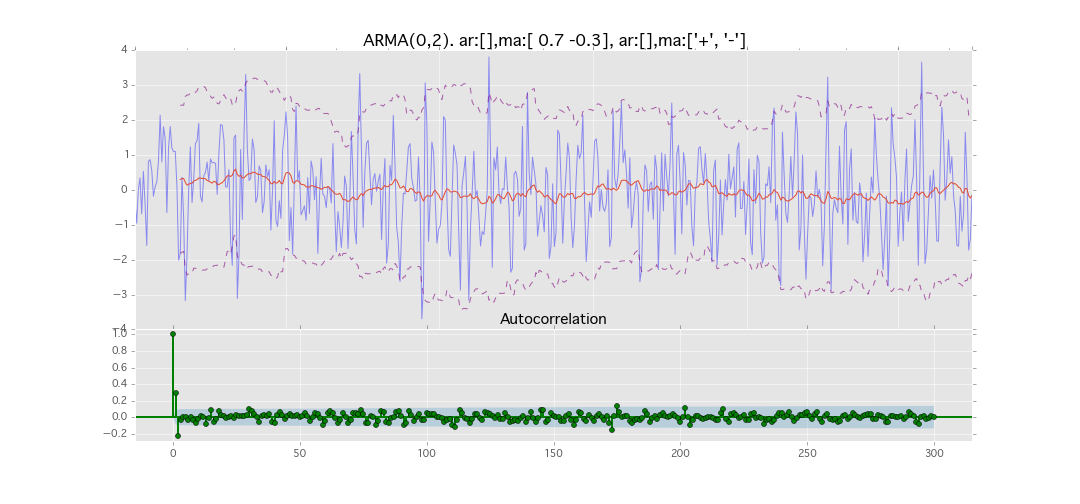
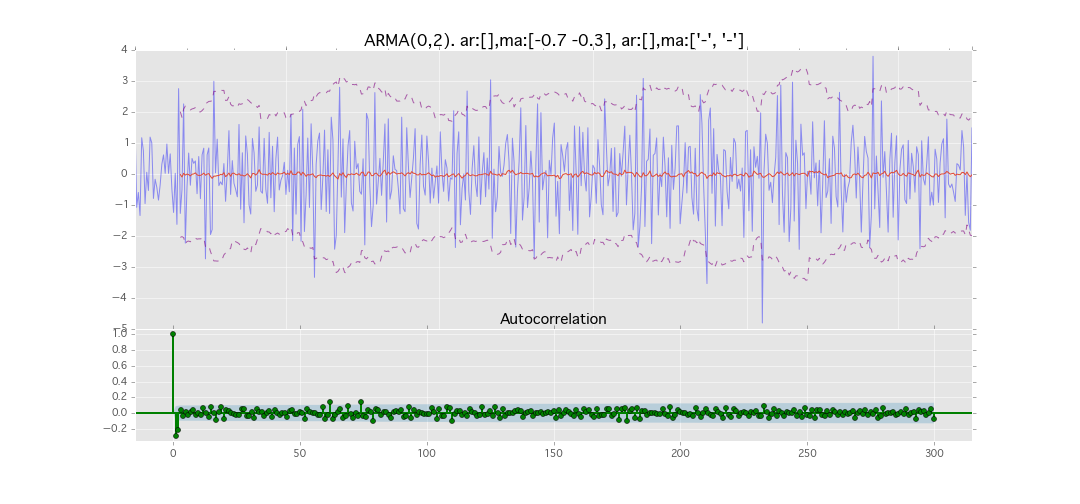
ARMA(0,2)
y_t = \varepsilon_t + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2}
パラメータ:
$\theta_1=0.7,\ \theta_2=0.3$
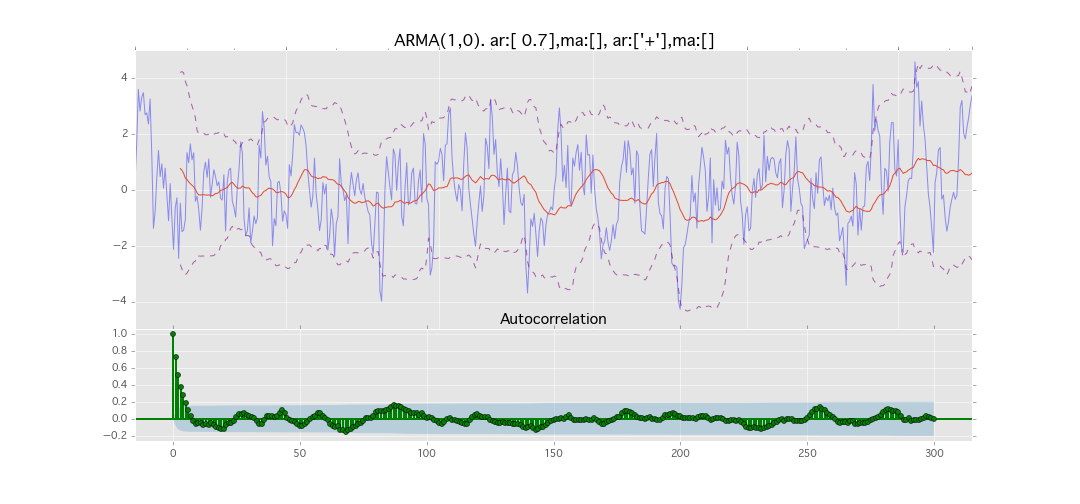
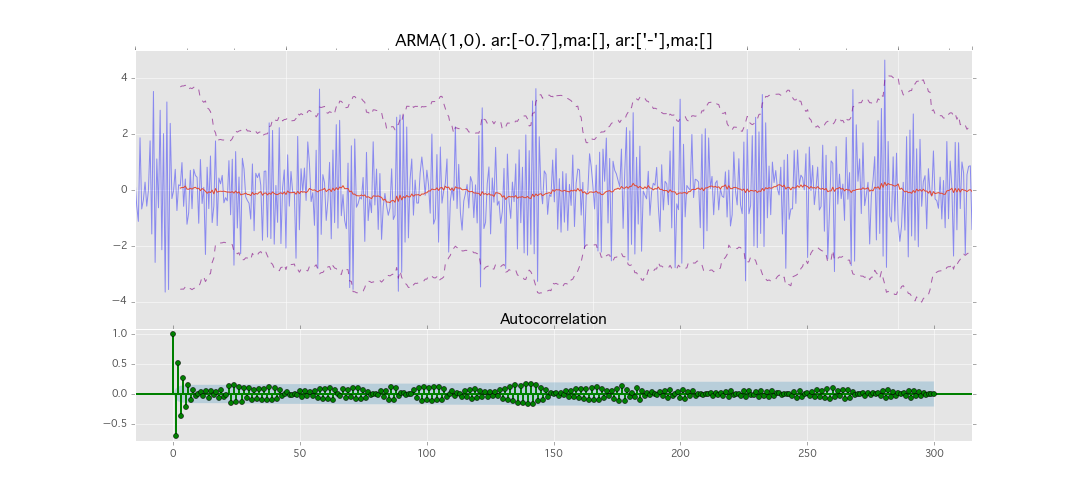
ARMA(1,0)
y_t = \varepsilon_t + \phi_1 y_{t-1}
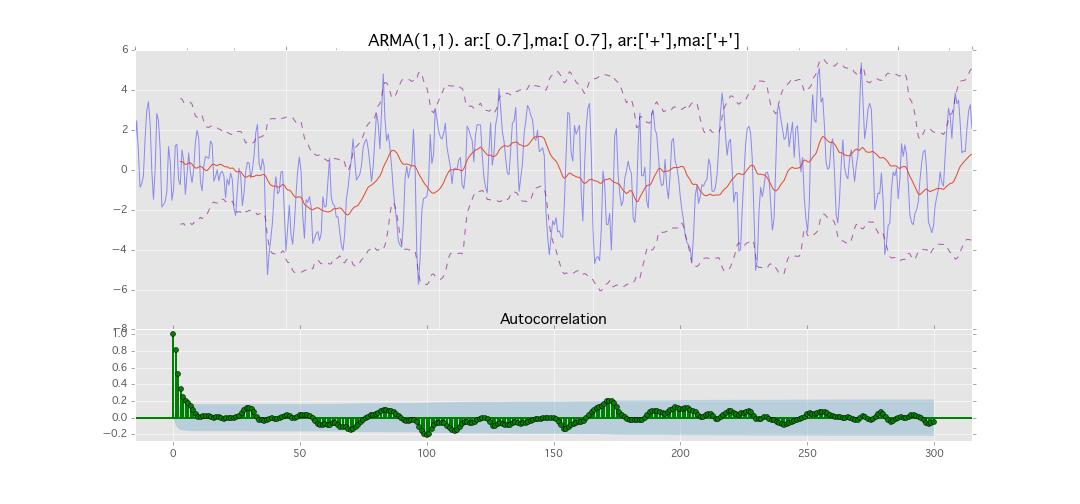
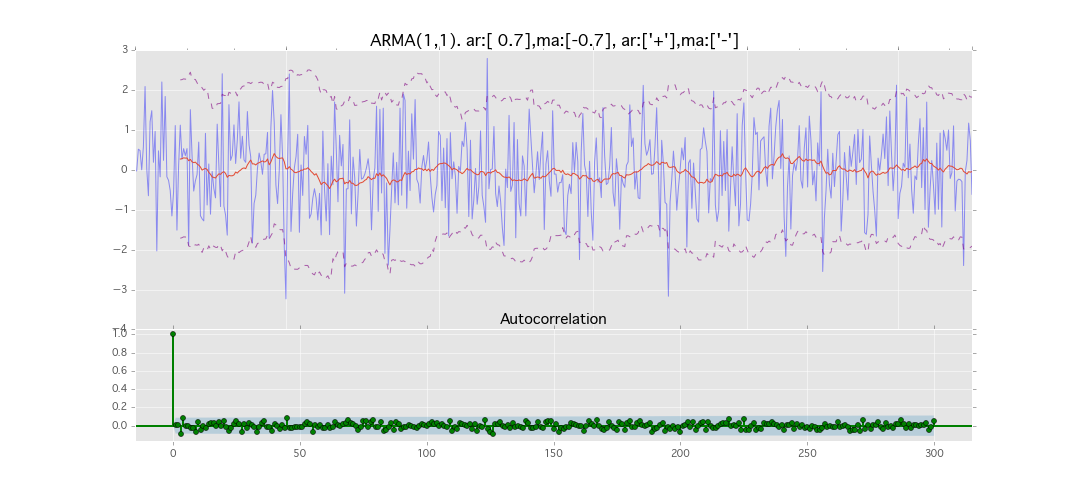
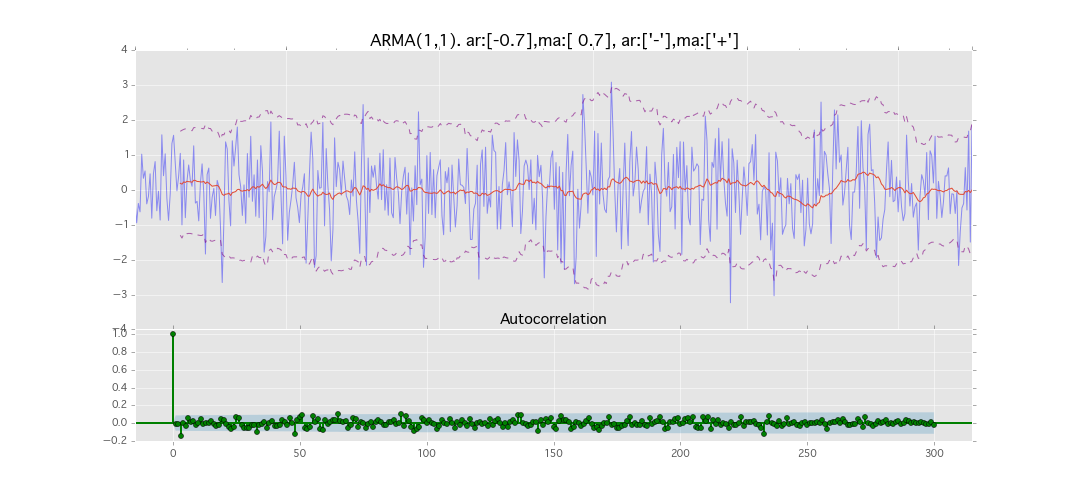
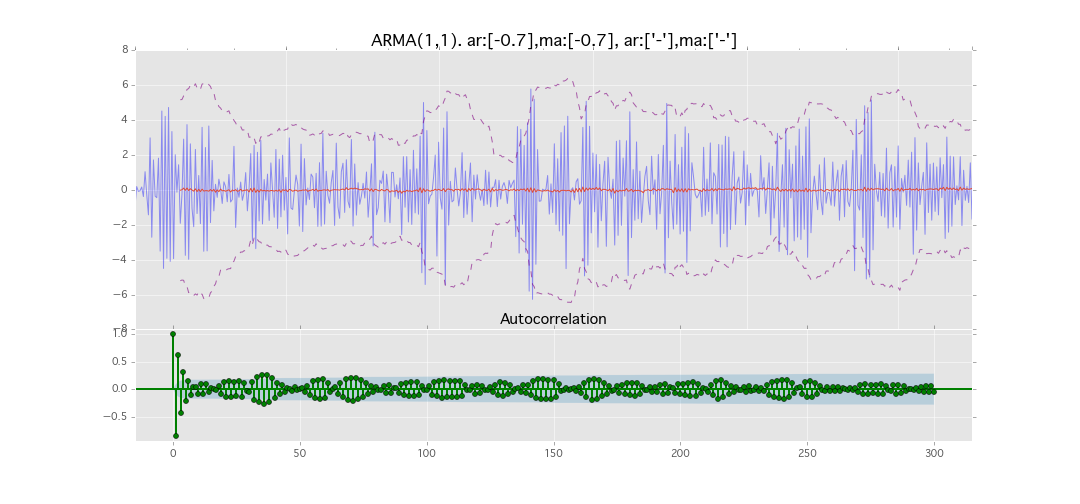
ARMA(1,1)
y_t = \varepsilon_t + \phi_1 y_{t-1} + \theta_1 \varepsilon_{t-1}
パラメータ:
$\phi_1=0.7,\ \theta_1=0.7$
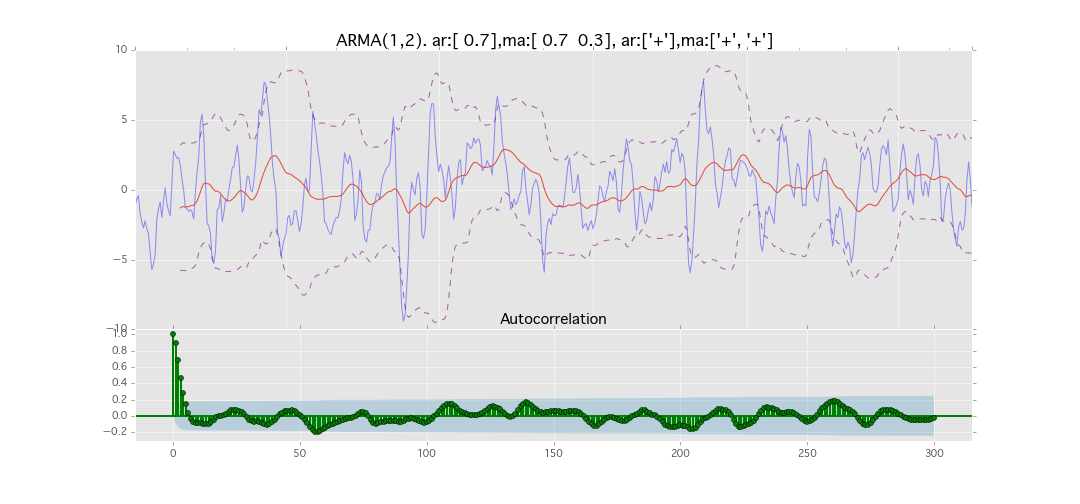
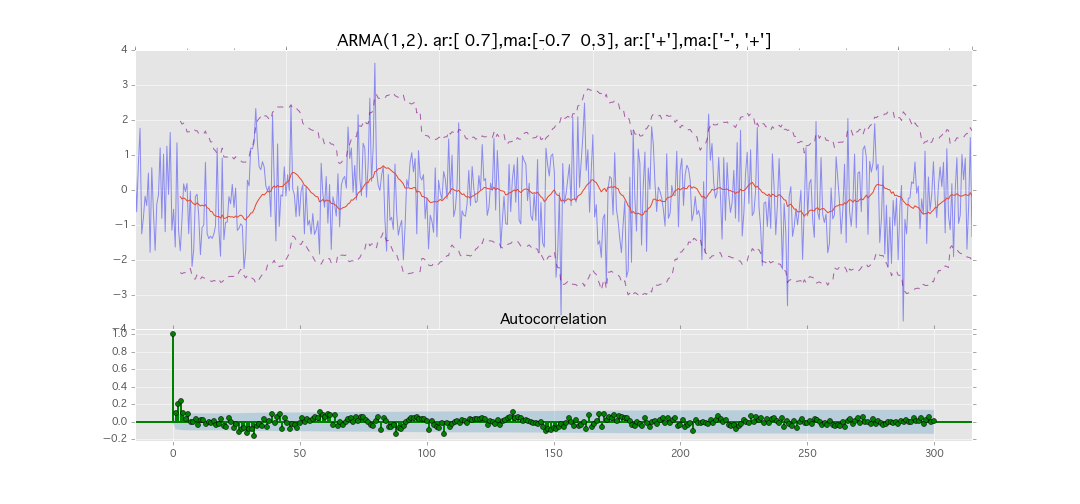
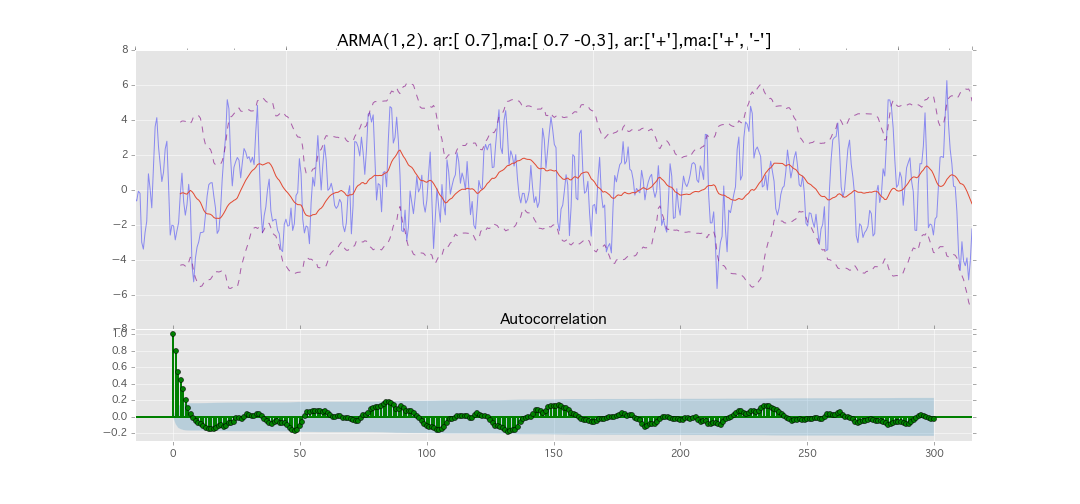
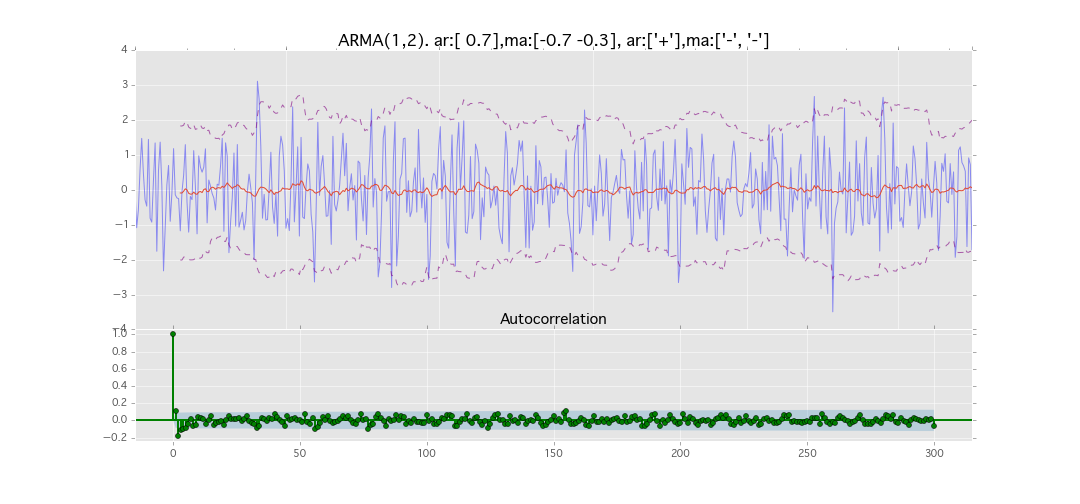
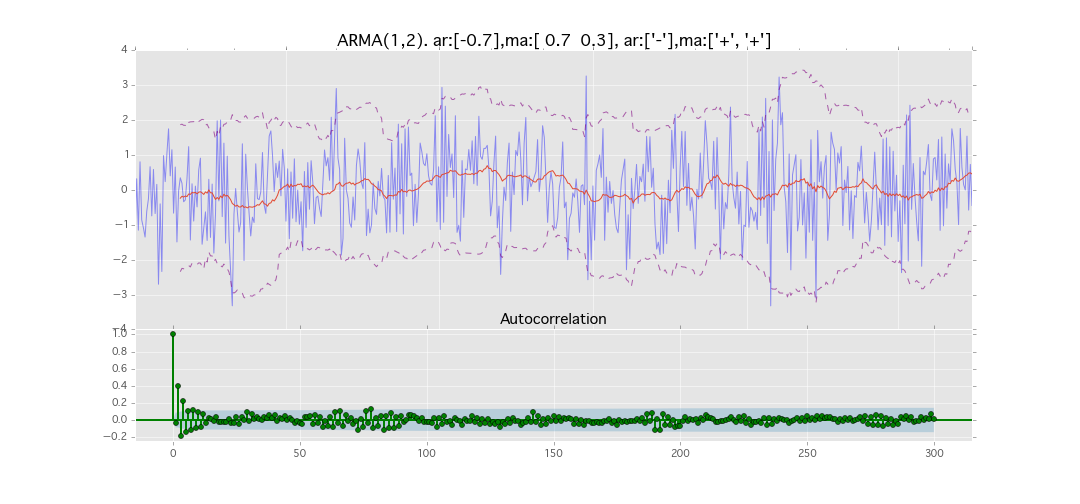
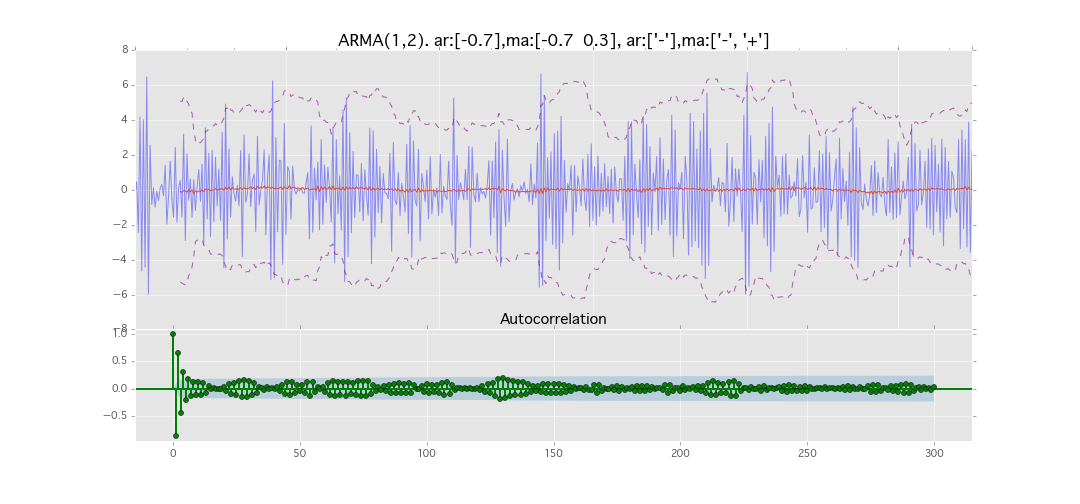
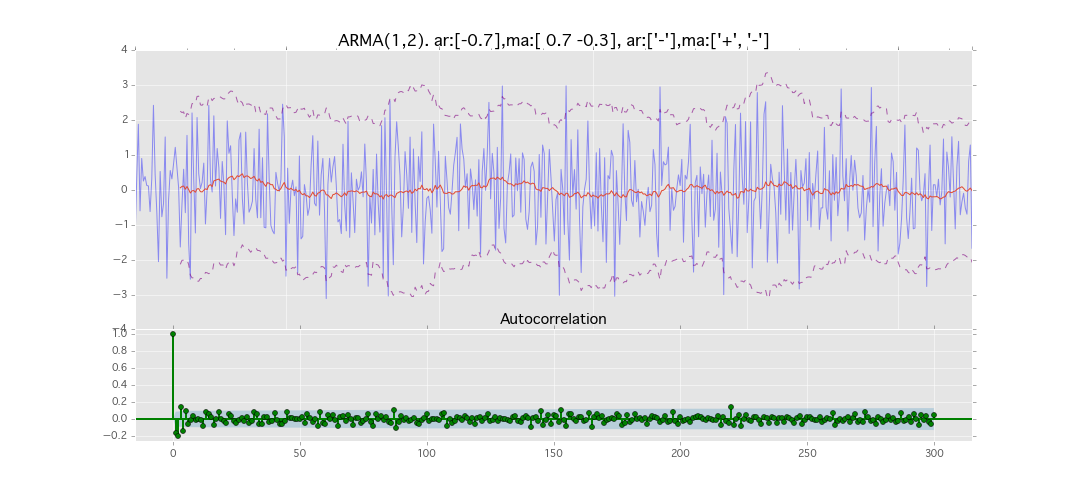
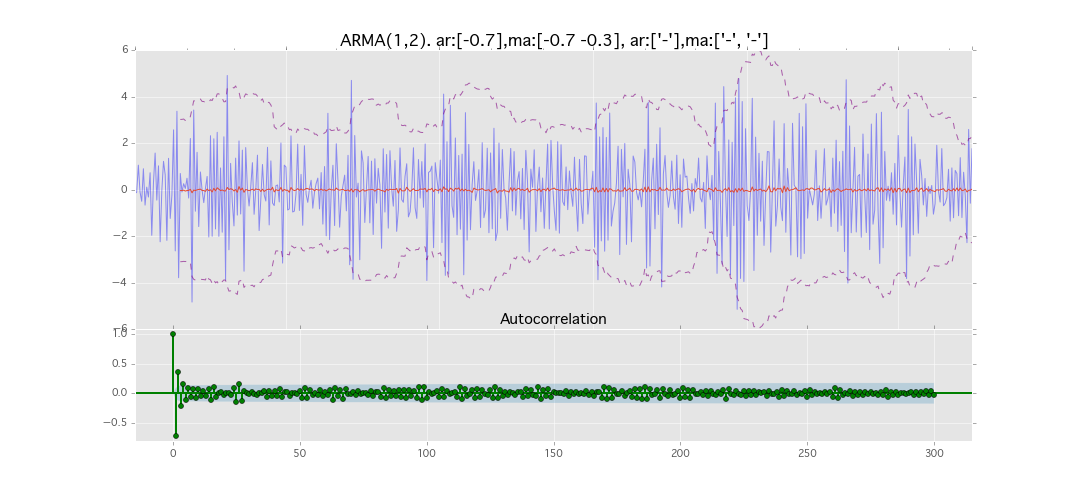
ARMA(1,2)
y_t = \varepsilon_t + \phi_1 y_{t-1} + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2}
パラメータ:
$\phi_1=0.7,\ \theta_1=0.7,\ \theta_2=0.3$
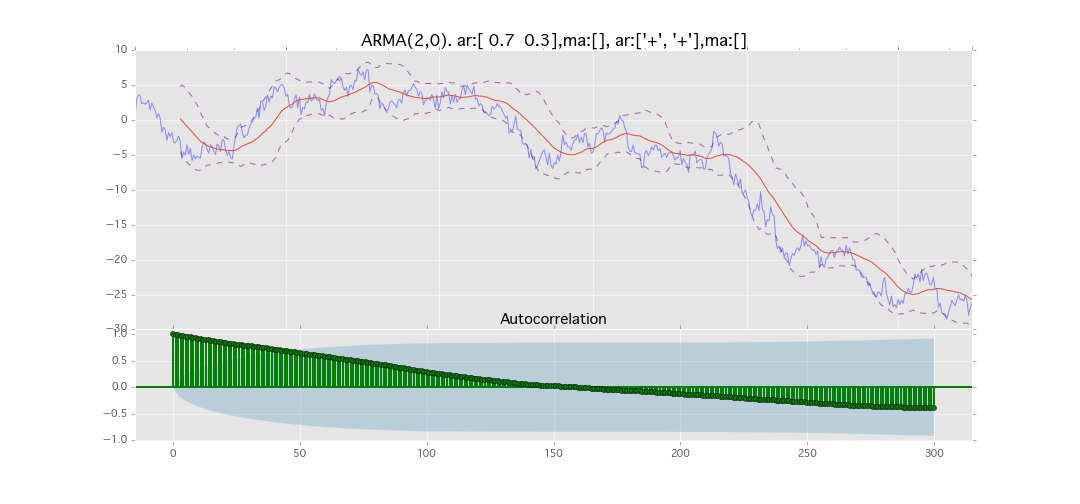
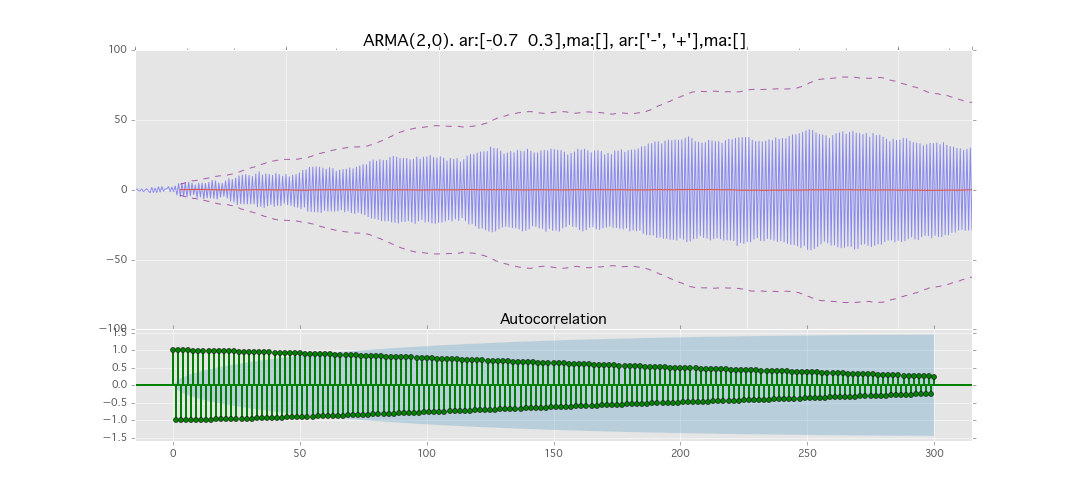
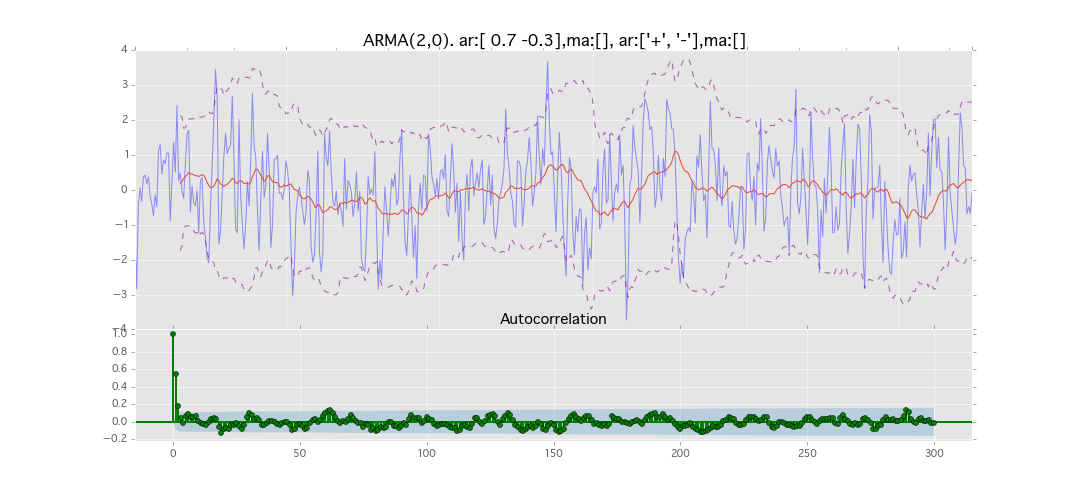
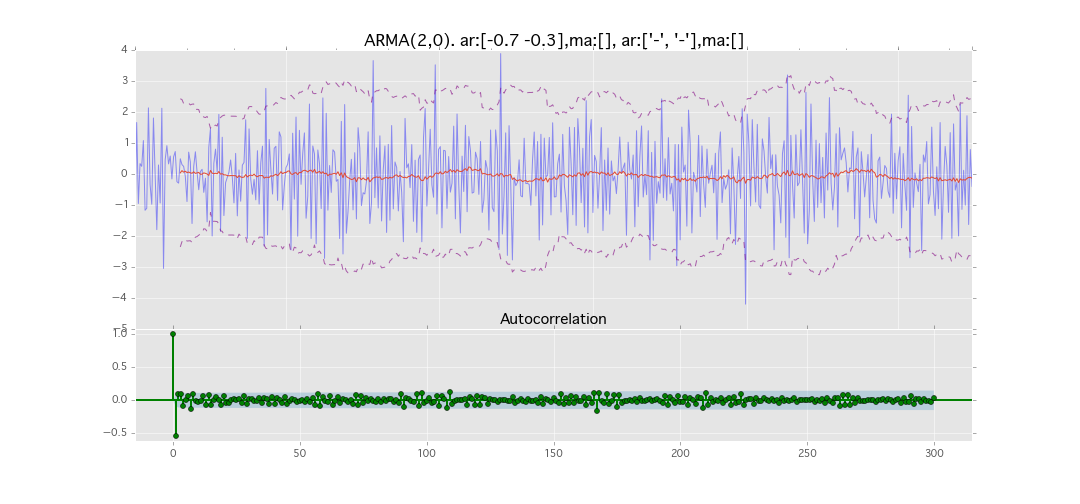
ARMA(2,0)
y_t = \varepsilon_t + \phi_1 y_{t-1} + \phi_2 y_{t-2}
パラメータ:
$\phi_1=0.7,\ \phi_2=0.3$
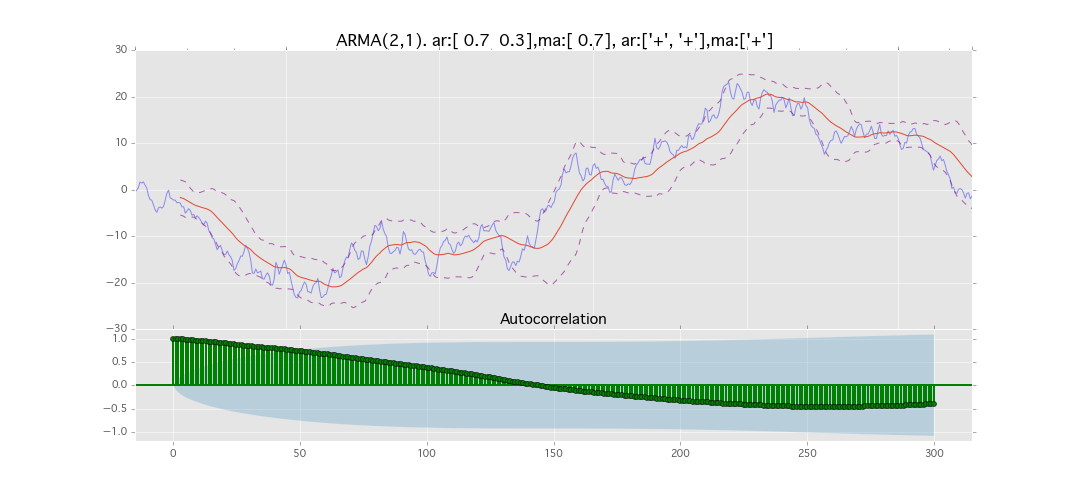
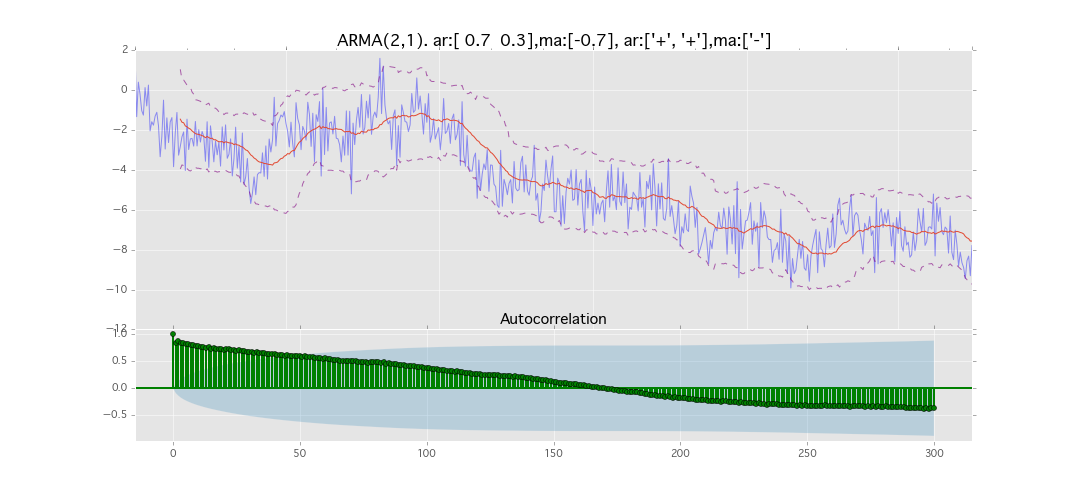
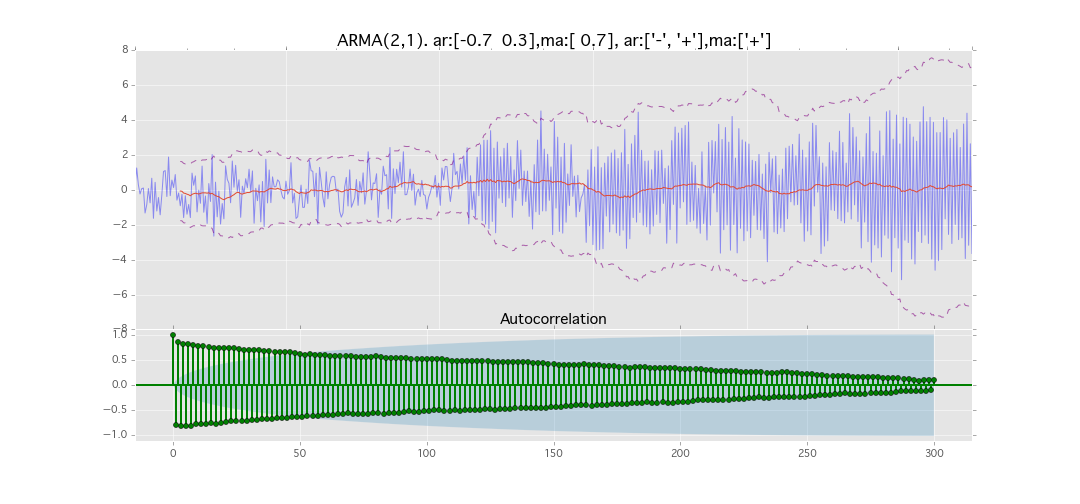
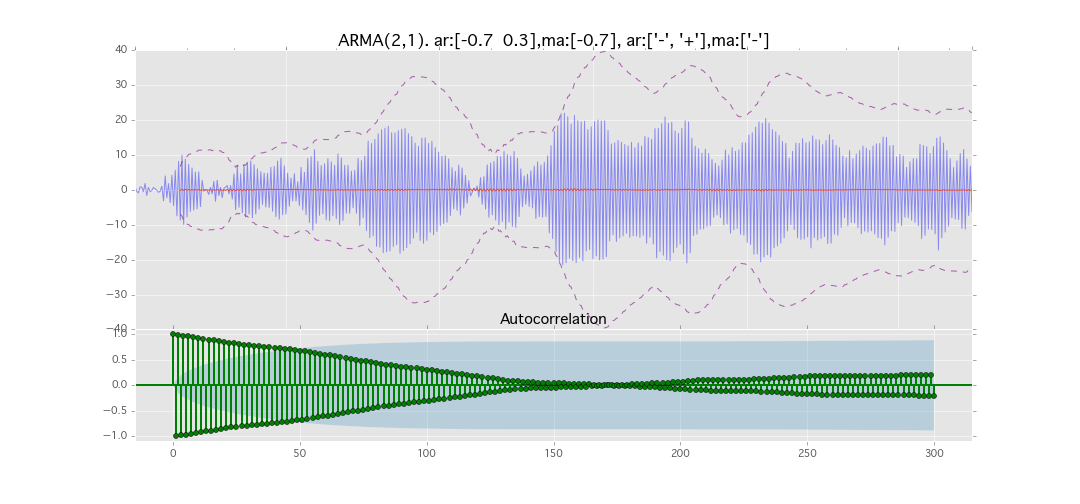
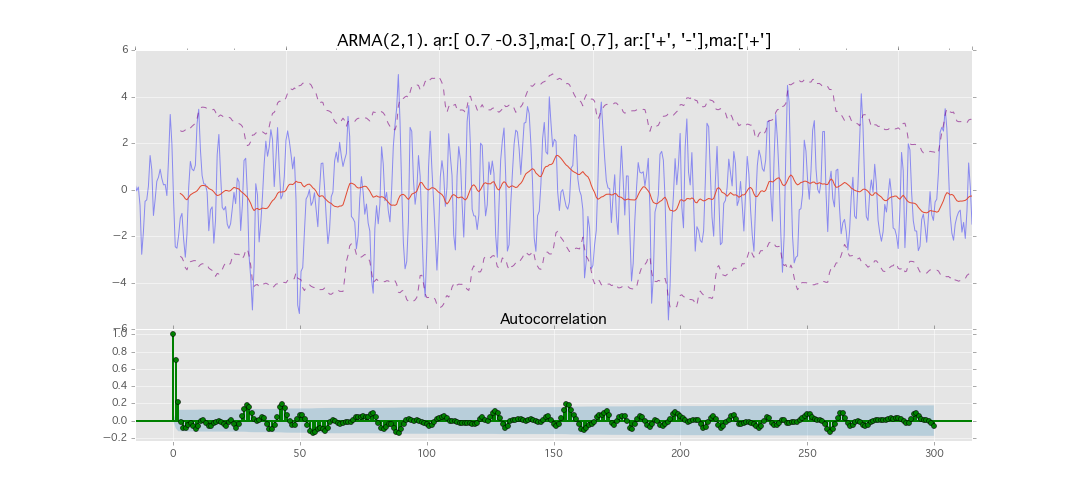
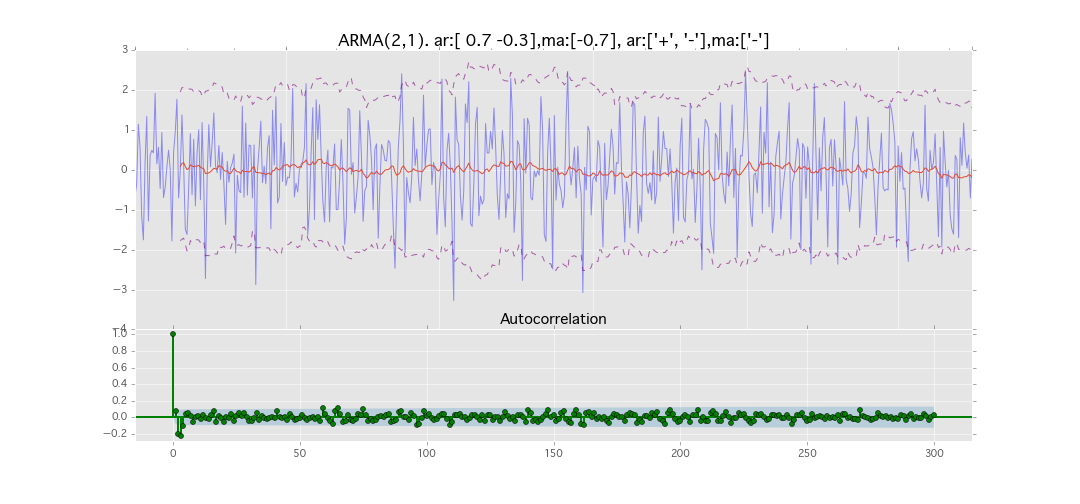
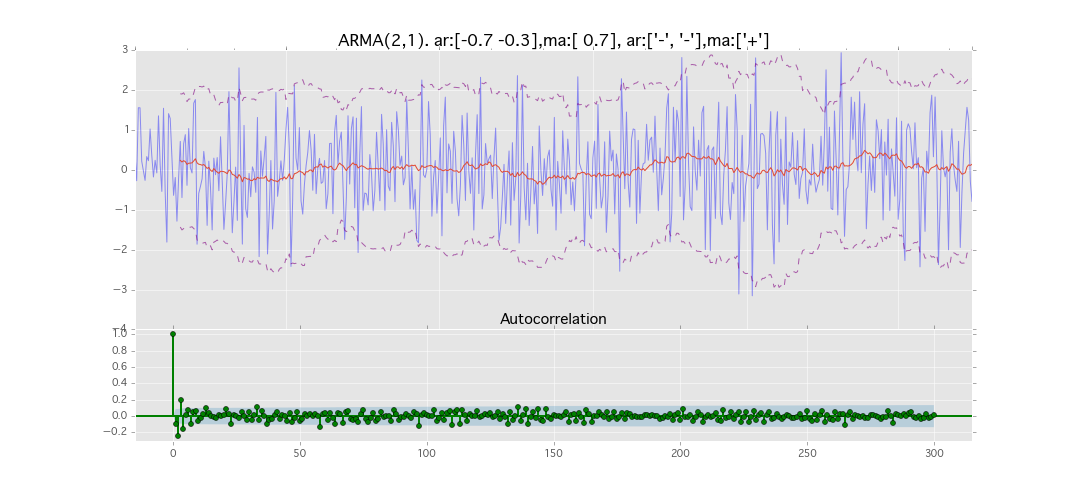
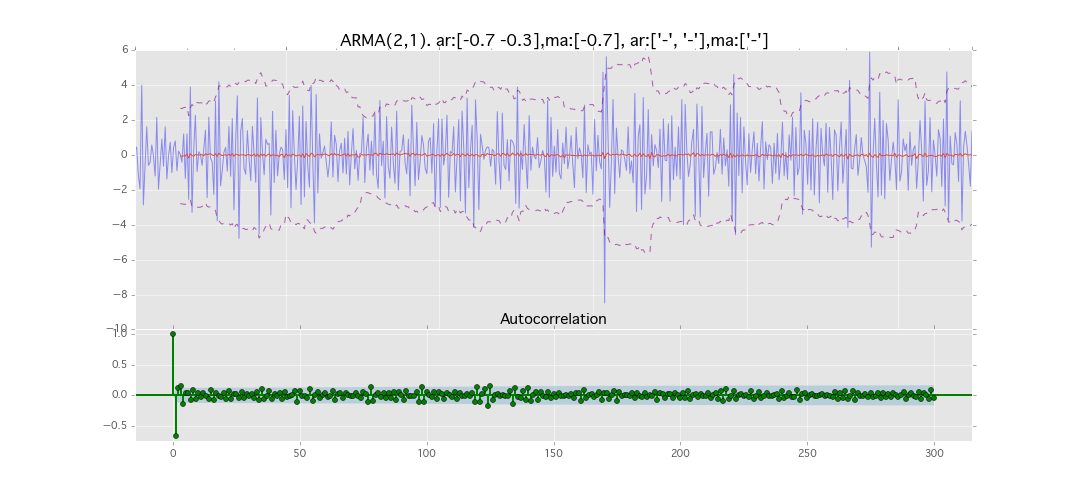
ARMA(2,1)
y_t = \varepsilon_t + \phi_1 y_{t-1} + \phi_2 y_{t-2} + \theta_1 \varepsilon_{t-1}
パラメータ:
$\phi_1=0.7,\ \phi_2=0.3\ \theta_1=0.7$
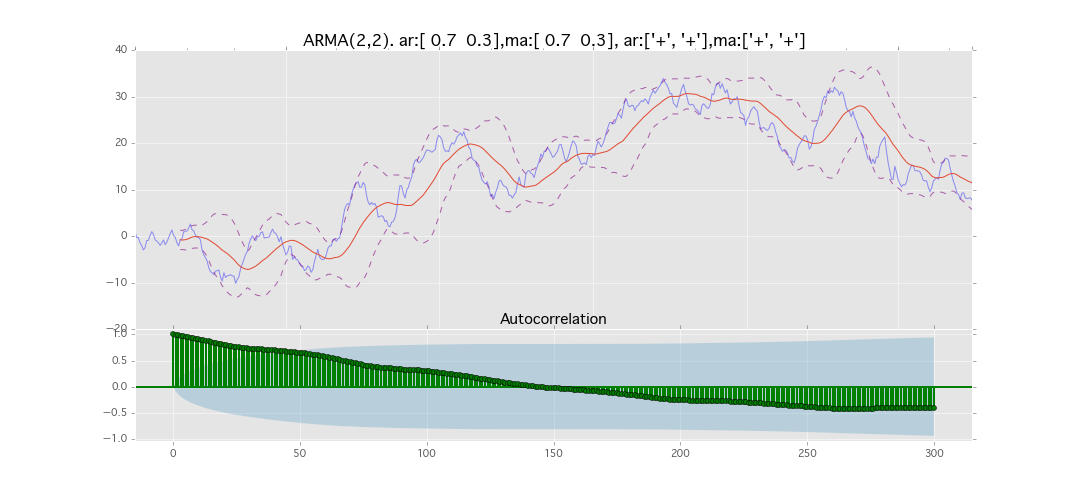
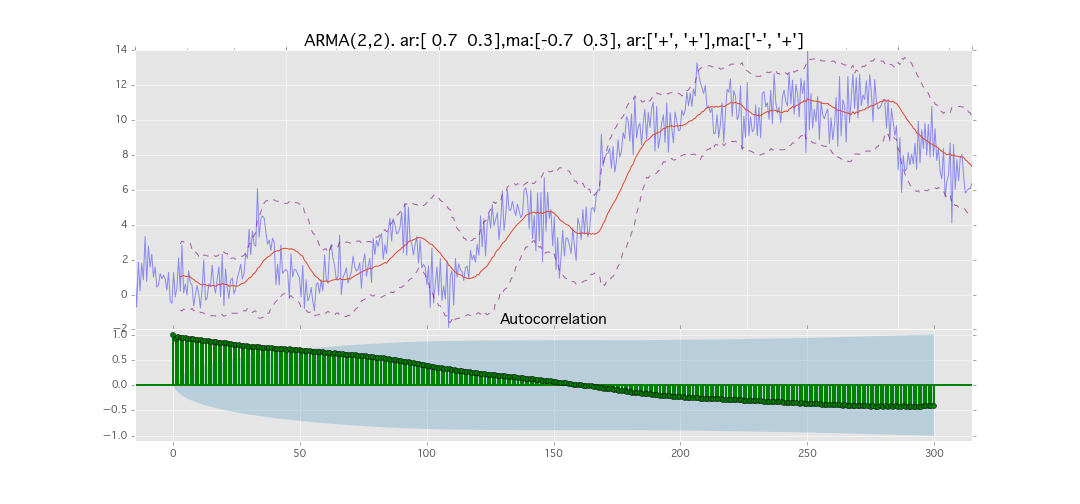
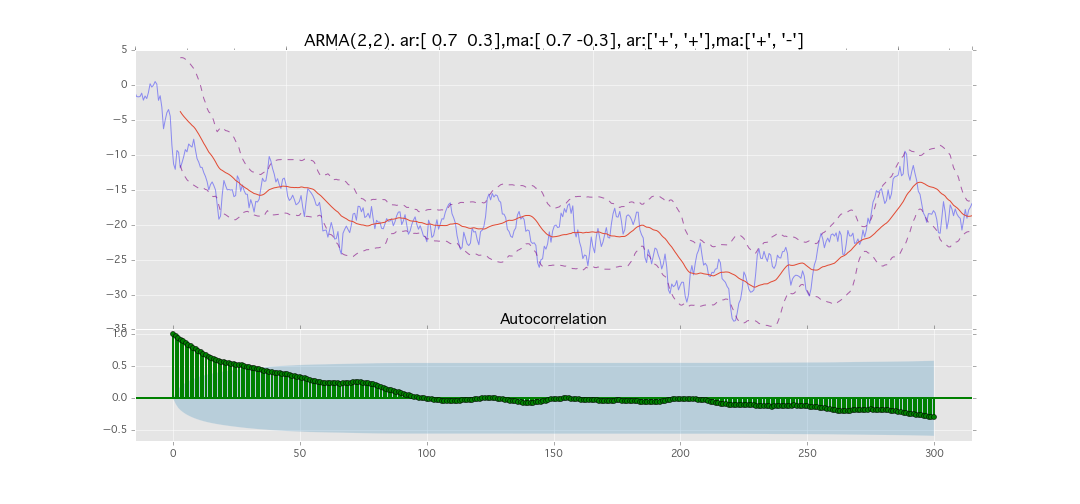
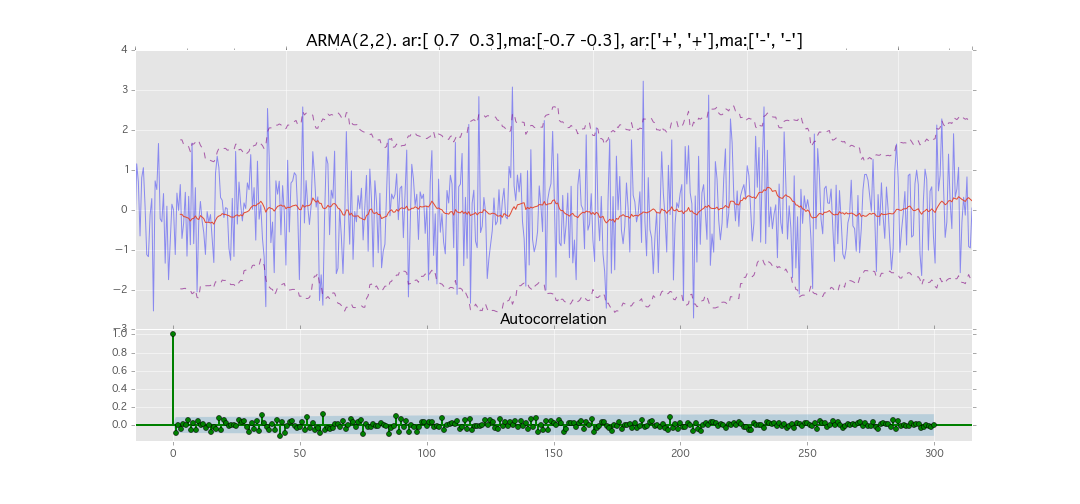
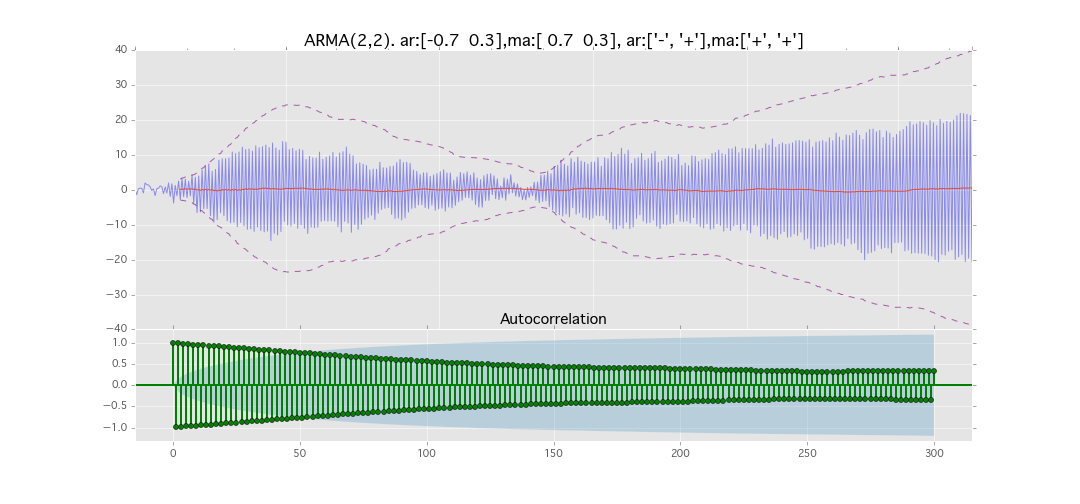
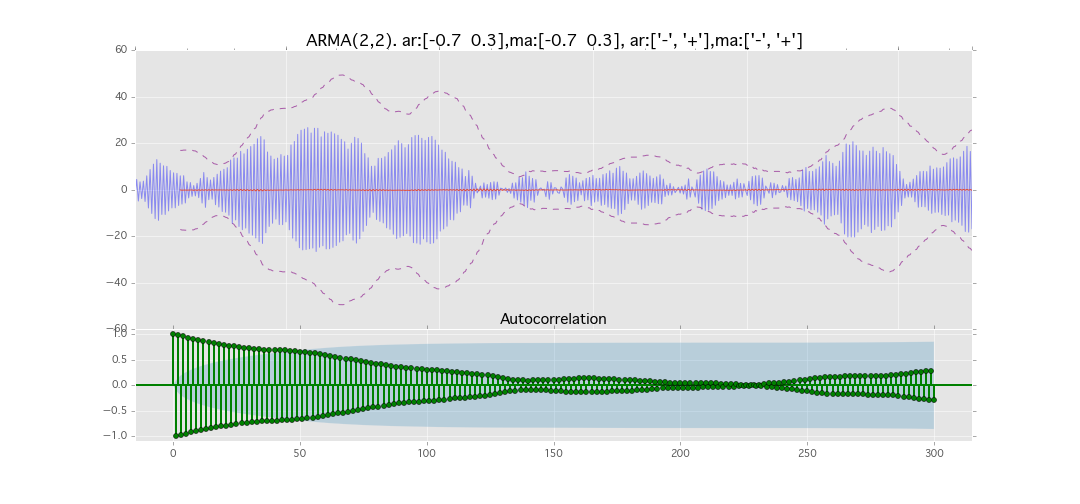
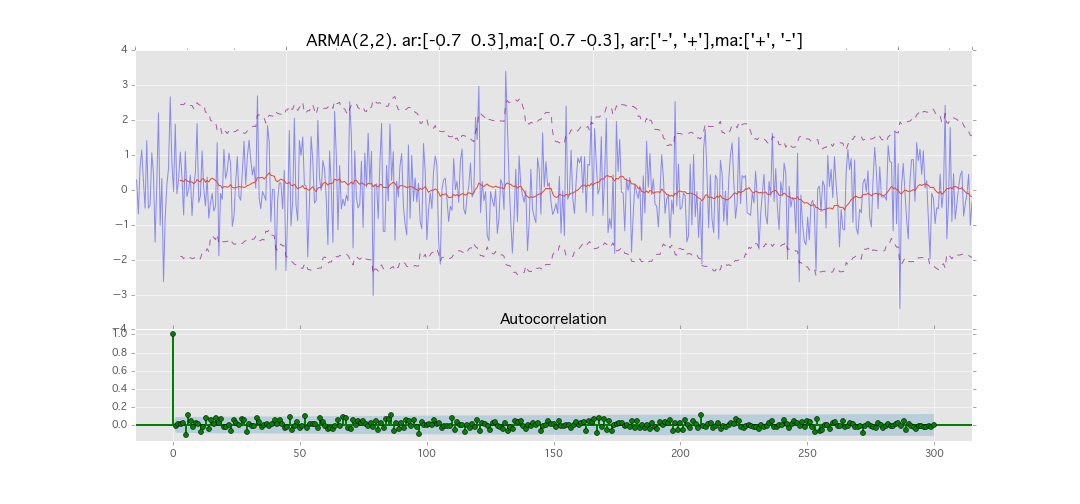
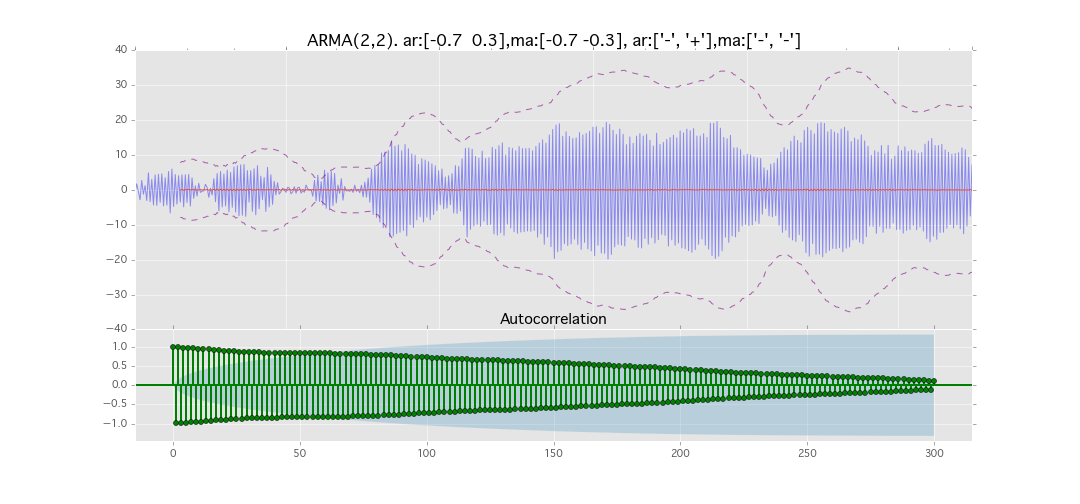
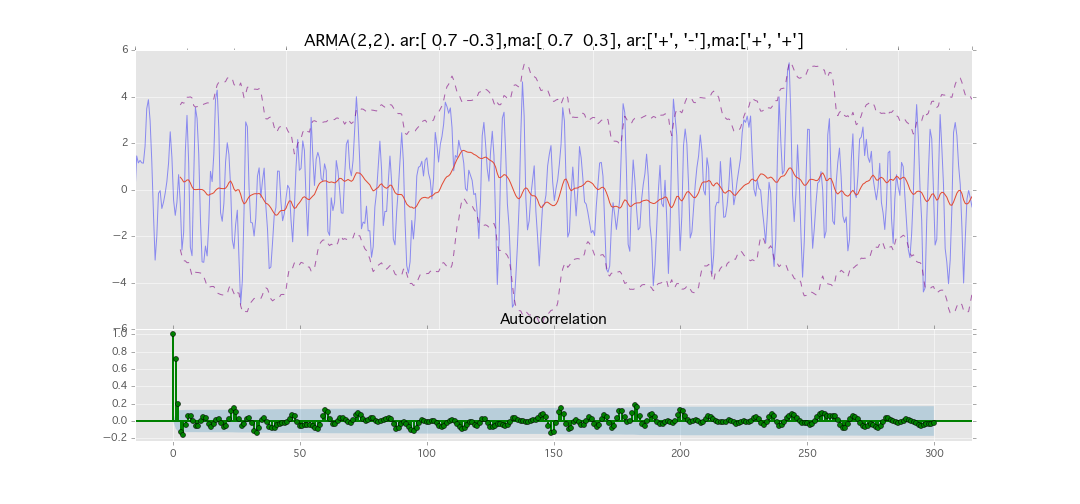
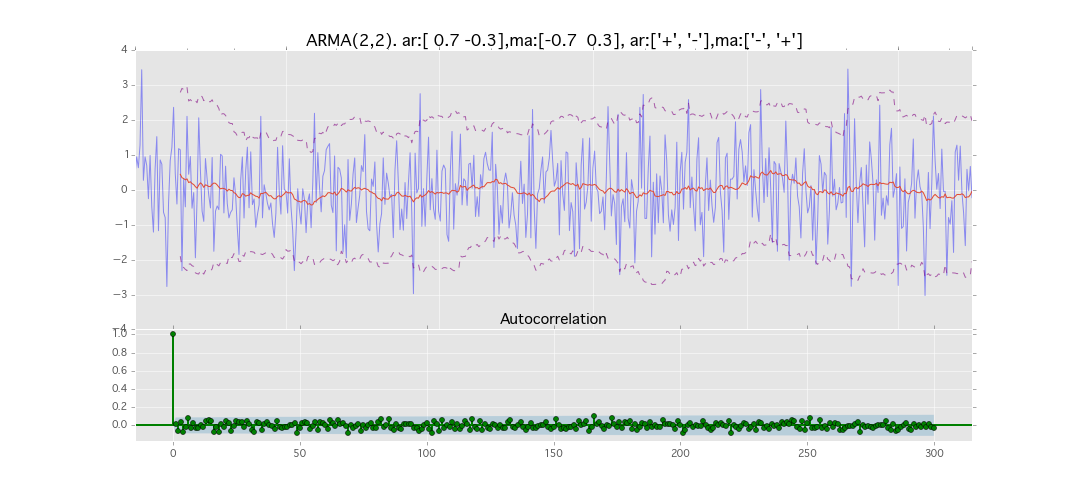
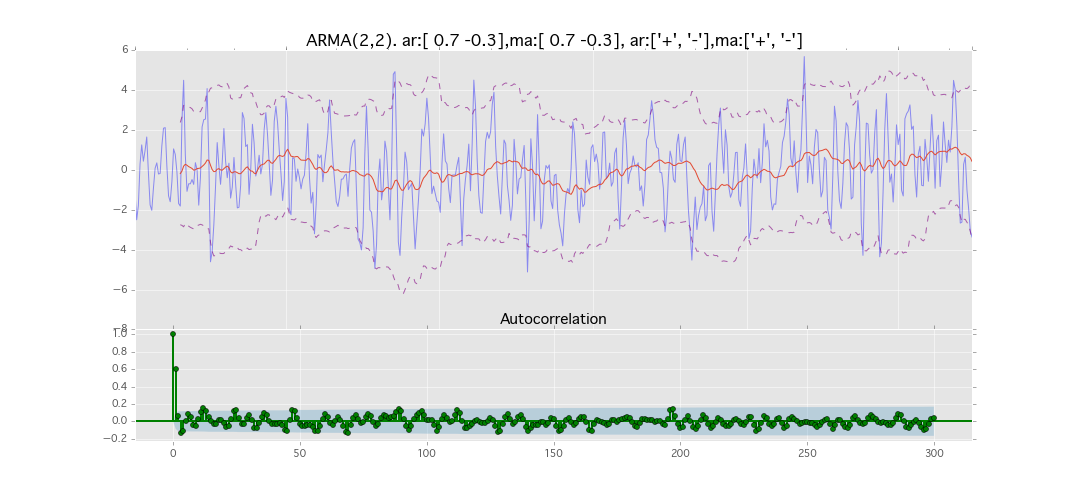
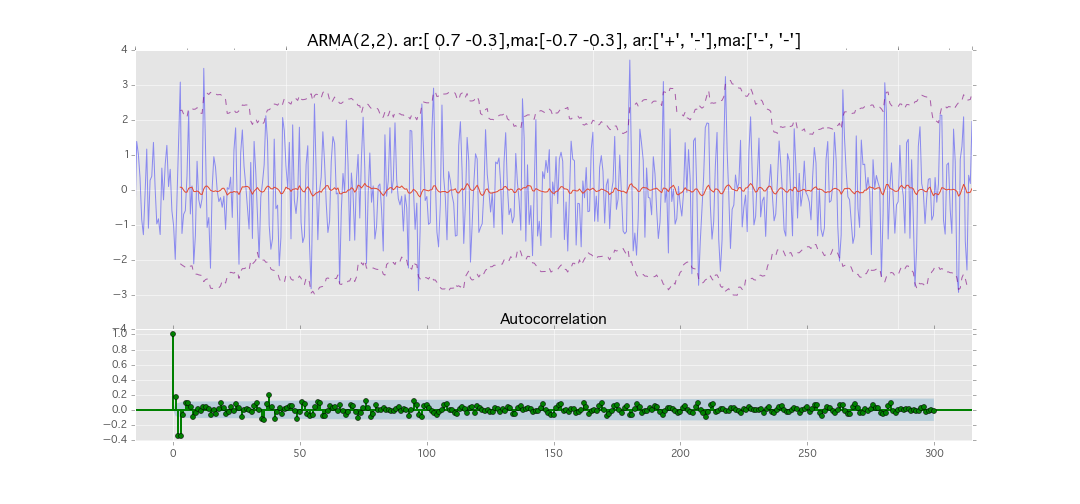
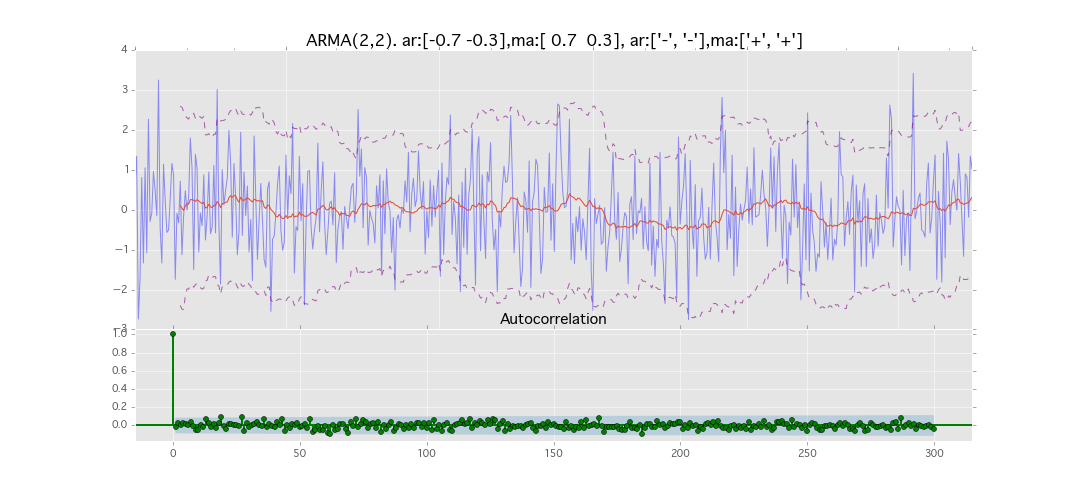
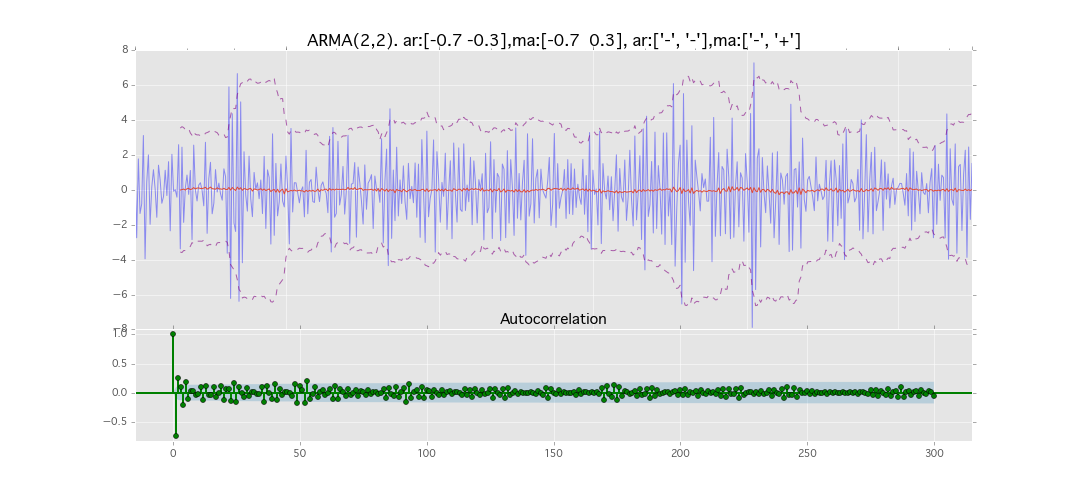
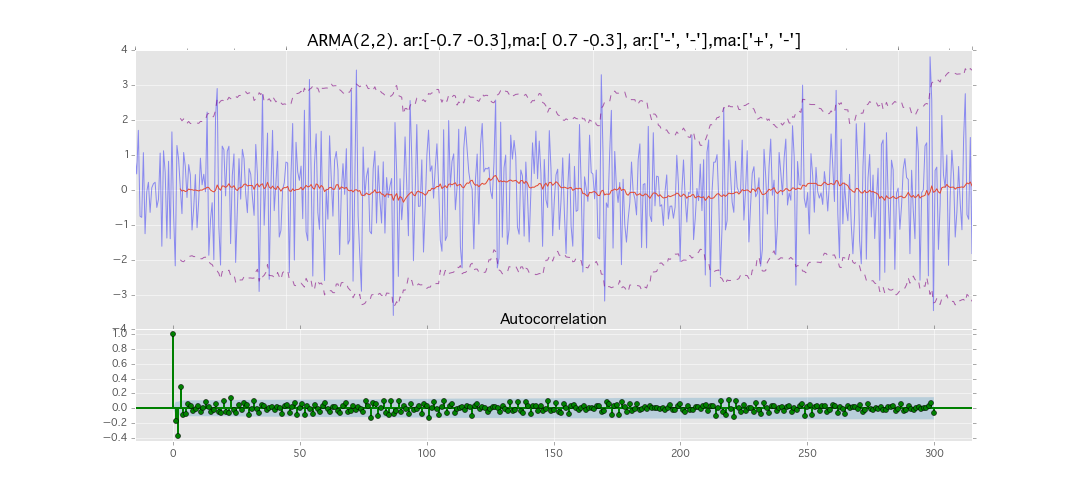
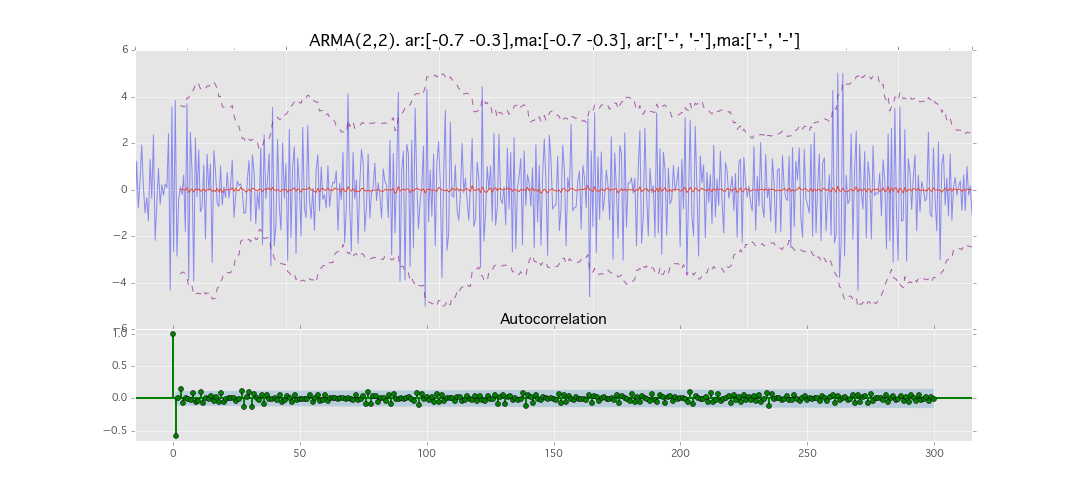
ARMA(2,2)
y_t = \varepsilon_t + \phi_1 y_{t-1} + \phi_2 y_{t-2} + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2}
パラメータ:
$\phi_1=0.7,\ \phi_2=0.3\ \theta_1=0.7,\ \theta_2=0.3$
描画用コード
PythonでARMAの人工データが作れるstatsmodelsを利用しました。
import numpy as np
import pandas as pd
import numpy.random as rd
import itertools, sys
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import gridspec
plt.style.use('ggplot')
from statsmodels.tsa.arima_process import arma_generate_sample
import statsmodels.api as sm
import statsmodels.tsa.stattools as stt
import statsmodels.graphics.tsaplots as tsaplots
def select_negative(l):
res = []
l = np.array(l)
n = len(l)
res.append(l)
l = np.array(l)
for i in range(n):
for j in itertools.combinations(range(n),i+1):
_l = l.copy()
_l[list(j)] = _l[list(j)] * -1
res.append(_l)
return res
cnt = 0
n = 3
nobs = 500
itrvl = 28
for len_ar in range(n):
for len_ma in range(n):
_ar_params = [.7, .3][:len_ar]
_ma_params = [.7, .3][:len_ma]
_ar_params = select_negative(_ar_params)
_ma_params = select_negative(_ma_params)
for i in _ar_params:
for j in _ma_params:
cnt += 1
ar_params = np.r_[1, -i]
ma_params = np.r_[1, j]
yy = arma_generate_sample(ar_params, ma_params, nobs)
ts = pd.Series(yy, index=pd.date_range('2010/1/1', periods=nobs))
ar_sign = ['+' if val >= 0 else '-' for val in i]
ma_sign = ['+' if val >= 0 else '-' for val in j]
plt.subplots(2, 1, sharex=True, figsize=(15,7))
gs = gridspec.GridSpec(2, 1, height_ratios=[5,2])
ax1 = plt.subplot(gs[0])
ax2 = plt.subplot(gs[1])
# ax1 --------
ts.plot(color="b", alpha=0.4, lw=1, ax=ax1,
title="ARMA({0},{1}). ar:{2},ma:{3}, ar:{4},ma:{5}".format(len_ar, len_ma, i, j, ar_sign, ma_sign))
ax1.set_title(ax1.get_title(), fontsize=16)
ts_mean = pd.rolling_mean(ts,itrvl)
ts_std = pd.rolling_std(ts,itrvl)
upper = ts_mean + ts_std * 1.96
lower = ts_mean - ts_std * 1.96
ts_mean.plot(ax=ax1)
upper.plot(figsize=(15,7), c="purple", alpha=.6, ax=ax1, linestyle='--')
lower.plot(figsize=(15,7), c="purple", alpha=.6, ax=ax1, linestyle='--')
# ax2 --------
tsaplots.plot_acf(ts ,ax=ax2, color="g", lags=300, lw=2)
plt.subplots_adjust(hspace=0)
plt.savefig('./ARMA_fig/ARMA_{}.png'.format(cnt))
plt.clf()
参考
StatsModels : Autoregressive Moving Average (ARMA): Artificial data
http://statsmodels.sourceforge.net/stable/examples/notebooks/generated/tsa_arma_1.html