【機械学習】「異常検知と変化検知 1章」ネイマンピアソンの補題の式の行間を埋めてみる
機械学習プロフェッショナルシリーズ「異常検知と変化検知」(http://ide-research.net/book/support.html#kodansha) 第1章「定理1.2 ネイマンピアソンの補題」の式展開の間を埋めてみる、という記事です。

自分なりの考えも入っているため、もしご指摘等あればコメントや、Tweetなどでご連絡いただけると嬉しいです。また、この記事内に誤りがあった場合は私@kenmatu4の責任ですので、著者の方に問い合わせを行わないよう御願い致します。

ネイマン・ピアソンの補題
観測値${\bf x'}$における異常度 $a({\bf x'}) = \ln{ p({\bf x'}|y=1, \mathcal{D}) \over p({\bf x'}|y=0, \mathcal{D}) }$ という定義は、一定の正常標本の下で異常標本精度を最大にするという意味で最適である。

最適な異常度、とは下記のように所与の観測値${\bf x'}$と正常標本精度$\alpha$のもとで、下記の積分を最大化するような関数$a({\bf x})$であるとし、、それを$a^*$と置きます。

a^* = \arg\max_a \int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ p({\bf x}|y=1, \mathcal{D})\ d{\bf x}　　　　　　　\cdots (*)

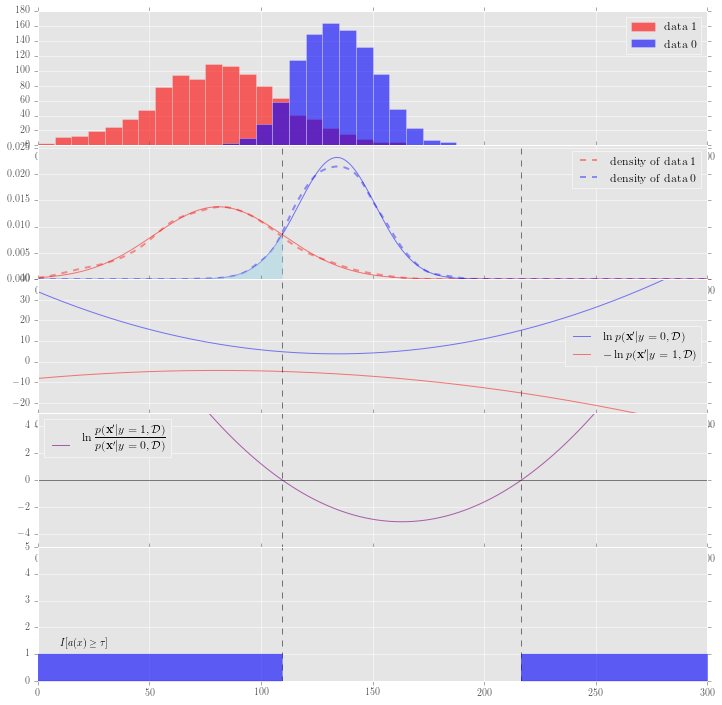
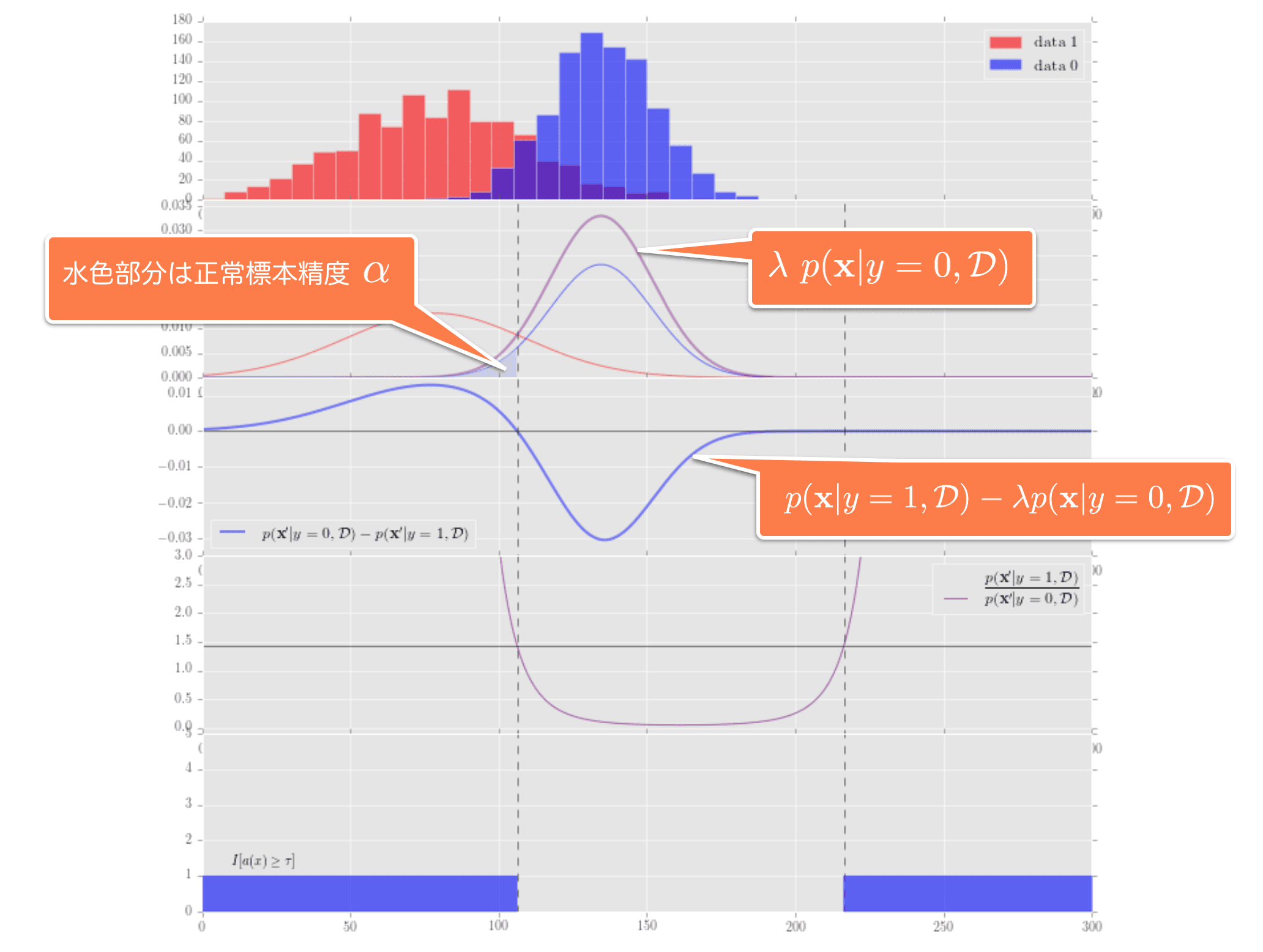
また、正常標本精度$\alpha$とは下記のグラフの上から２つ目の水色の面積のことなので、$\alpha$を確定させると面積が決まり、異常度 $a({\bf x})$の定義の仕方によってその面積の取り方（片側とか、両側とか、その他いろいろ同じ面積でも取り方を選べるので）がきまり、結果${\bf x'}$が決まります。

いま、軸が４つあり、

観測値 :　${\bf x},\ {\bf x'}$
異常度 :　$a({\bf x}),\ \tau,\ \tau_\alpha$
確率密度:　$p({\bf x}|y=0, \mathcal{D}), p({\bf x}|y=1, \mathcal{D}),$
確率(精度):　$\alpha$

であることに注意して、別な次元のデータで計算してしまわないように意識することが重要かなと思っています。（「確率」の部分は確率密度、と確率、があることに注意です。）

下記の図は、横軸は全て観測値、縦軸は上から、２つ目が確率(密度)、４つ目が異常度になります。$\alpha$は２つ目のグラフの面積の部分になりますね。

(*)式の$\max(\cdot)$のなかを最大化するので、下記の問題を解くことで答えが得られます。この制約条件は正常標本精度が$\alpha$であることを満たすための条件です。

\int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ p({\bf x}|y=1, \mathcal{D})\ d{\bf x}　\rightarrow \max \\
{\rm subject\ to} \int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ p({\bf x}|y=0, \mathcal{D})\ d{\bf x} = 1 - \alpha

ラグランジュの未定乗数方を使って条件つき最大化を行います。対象の関数を$L$と置くと、

L = \int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ p({\bf x}|y=1, \mathcal{D})\ d{\bf x} - \lambda \left( \int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ p({\bf x}|y=0, \mathcal{D})\ d{\bf x} - ( 1 - \alpha)  \right)

簡単化のために

\beta = I[a({\bf x}) \ge \tau_\alpha] \\
p_0 = p({\bf x}|y=0, \mathcal{D}) \\
p_1 = p({\bf x}|y=1, \mathcal{D})

と置くと、


L = \int_{-\infty}^{\infty}  \beta\ p_1 \ d{\bf x} - \lambda \left( \int_{-\infty}^{\infty}  \beta\ p_0\ d{\bf x} - ( 1 - \alpha)  \right) \\
= \int_{-\infty}^{\infty} \beta (p_1 - \lambda p_0)\ d{\bf x}   + \lambda( 1 - \alpha)

一番後ろの$- \lambda( 1 - \alpha) $は$a({\bf x})$の最大化に関して定数項のため無視すると、p14にある式、

\Psi[a|\lambda] = \int_{-\infty}^{\infty}  I[a({\bf x}) \ge \tau_\alpha]\ \{ p({\bf x}|y=1, \mathcal{D}) - \lambda p({\bf x}|y=0, \mathcal{D})\}\ d{\bf x}

が、得られます。

この関数を最大化とは、下記のグラフの3つ目のグラフの積分、つまり面積の最大化になります。

これは、関数が負の値をとる領域を除くように指示関数 $I[a({\bf x}) \ge \tau_\alpha]$をとればよいので、$a({\bf x})$がちょうどこの関数 ${ p({\bf x}|y=1, \mathcal{D}) - \lambda\ p({\bf x}|y=0, \mathcal{D}) }$が正の値をとる領域を示すようになればよいと考えられます。

また、$\lambda$は正常標本精度$\alpha$をキープするためのクッションとなる役目を果たし、３つめのグラフにあるように${ p({\bf x}|y=1, \mathcal{D}) - \lambda\ p({\bf x}|y=0, \mathcal{D}) }=0$を満たす点を調整する役割を果たしています。

その上で、この曲線が正の値をとる領域を指し示すには

 {p({\bf x'}|y=1, \mathcal{D}) \over p({\bf x'}|y=0, \mathcal{D})} \ge \lambda

を満たしていればよいので、もうひとつ指示関数があったとして

I\left[{p({\bf x'}|y=1, \mathcal{D}) \over p({\bf x'}|y=0, \mathcal{D})} \ge \lambda \right]

が、この条件を満たしている指示関数になります。ここで元の指示関数

I[a({\bf x}) \ge \tau_\alpha]

と見比べると、

a({\bf x'}) = {p({\bf x'}|y=1, \mathcal{D}) \over p({\bf x'}|y=0, \mathcal{D})} \\
\lambda =  \tau_\alpha

としても、この条件を満たしていると言えます。よって、

a({\bf x}) = {p({\bf x}|y=1, \mathcal{D}) \over p({\bf x}|y=0, \mathcal{D})}

を異常度として適用した場合に、最適なものであるという必要十分条件を満たしていると言えるのです。¹
また、単調増加関数である$\ln(\cdot)$をこれに適用しても、同様に成り立ち、異常度としての役割は同じように果たせるため、これを適用するとネイマンピアソン決定則に使われる異常度

a({\bf x}) = \ln { p({\bf x}|y=1, \mathcal{D}) \over p({\bf x}|y=0, \mathcal{D})}

が最適な異常度の条件を満たしていることが言えることがわかりました。

参考図書

「異常検知と変化検知」　井手剛、杉山将著　（機械学習プロフェッショナルシリーズ）
　　http://ide-research.net/book/support.html

ただし、他にもこの最適を満たした異常度に使える館数の存在は否定しておらず、唯一のものであるとは言っていないのでは、と考えています。 ↩