ランダムフォレストに関する解説を読んでいるとよく遭遇するOOB(Out-Of-Bag)、その詳細に迫ります。
ブートストラップサンプリング
$N$ 個の訓練標本 $\{\boldsymbol{x}_i, y_i \} _{i=1}^N$ から重複を許してランダムに同じだけの数$N$個を選ぶことで、訓練標本集合を作る方法をブートストラップサンプリングと呼びます。ランダムフォレストではこのブートストラップサンプリングで作った$M$個の訓練標本で多数の決定木を作ることから「フォレスト」という名称がついています。

このとき、$N$個から重複ありで$N$個選ぶので、中には選ばれなかったデータがあります。これをOOB(Out-Of-Bag)と呼びます。ランダムフォレストのエラーの評価に使われたりします(ココなど) $i$番目のデータ$ ( \boldsymbol{x}_i, y_i )$に着目すると、$M$この標本セットのうち、幾つかでは使われていないことになるのです。そこで、その使われなかった木だけを集めてきて部分木を構成し、それで精度を評価するのが、OOB誤り率と呼ばれるものです。
このOOB、どれくらいの量になるかというと、およそ、36%のサンプルが1つの標本を作るときに使われないことになるそうなのですが、本当でしょうか。調べてみましょう。
シミュレーションで試してみる
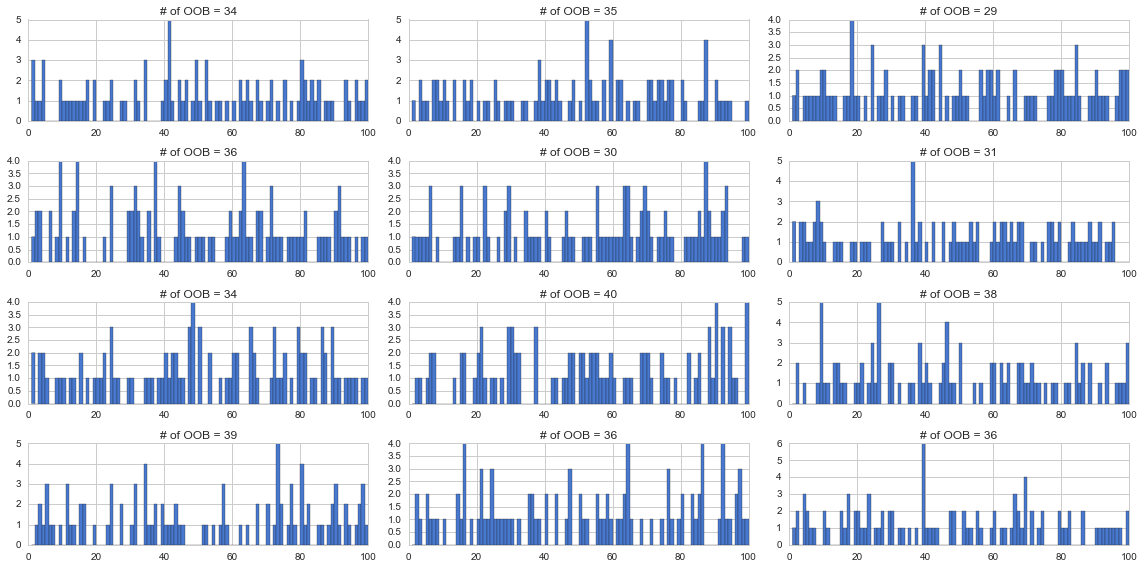
試しに100個のデータから100個ランダムに選んだ結果を12回繰り返し、それぞれカウントして棒グラフを書いてみたのが下記です。各グラフのタイトルに選ばれなかったデータの数つまりOOBの数を記載しています。だいたい30中盤くらいの個数になっていると言えるのではないでしょうか。12個の平均OOB数は約34.83でした。確かに3割程度ですね。
rd.seed(71)
n_data = 100
result = np.zeros((12, n_data))
OOBs = []
plt.figure(figsize=(16,8))
for i in range(12):
ax = plt.subplot(4,3,i+1)
result[i] = rd.randint(1,n_data+1, n_data)
res = plt.hist(result[i], bins=range(1,n_data+1))
cnt = Counter(res[0])
plt.title("# of OOB = {}".format(cnt[0]))
OOBs.append(cnts[0])
plt.xlim(0, n_data)
plt.tight_layout()
print("Average of OOB = {}".format(np.mean(OOBs)))
理論的に考えてみる
あるサンプル$\boldsymbol{x}_i$が選ばれない確率を考えます。全部でデータは$N$個あるので、今注目しているデータが選ばれないということは、データの個数から自分自身の1個分を引いた$N-1$通りなので、確率は
\left( { N-1 \over N} \right)
です。
いま、$N$個の標本を選ぶので、$N$回個のデータセットからサンプリングを行うので、$N$乗することになります。
\left( { N-1 \over N} \right)^{N} = \left( 1-{ 1 \over N} \right)^{N}
これを計算すると、実は$N$を大きくすると、約36%になるのです。やってみましょう。
res_list = []
for i in range(6):
n_data = 10**i
result = (((n_data-1)/n_data)**n_data)*n_data
res_list.append([n_data, result, result/n_data])
df = pd.DataFrame(res_list)
print( tabulate(df, ["データ数", "選ばれなかった列数" , "選ばれなかった率"], tablefmt="pipe"))
| データ数 | 選ばれなかった列数 | 選ばれなかった率 | |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 10 | 3.48678 | 0.348678 |
| 2 | 100 | 36.6032 | 0.366032 |
| 3 | 1000 | 367.695 | 0.367695 |
| 4 | 10000 | 3678.61 | 0.367861 |
| 5 | 100000 | 36787.8 | 0.367878 |
ちゃんと36%付近に収束しているようですね ![]()
ネイピア数eとの関係
@nykergoto さんにネイピア数との関連をご教授いただきました。ありがとうございます!
ちなみにこの確率、
\left( 1-{ 1 \over N} \right)^{N}
ネイピア数$e$の定義、
\lim_{n \rightarrow \infty} \left( 1 + { 1 \over N} \right)^{N}
に似ていますよね。ここで$t=N-1$と変数変換すると
\left( { N-1 \over N} \right)^{N} = \left( { t \over t+1} \right)^{t+1} = \left( { t+1 \over t} \right)^{-(t+1)} = \left( 1 + { 1 \over t} \right)^{-(t+1)} = \left( \left( 1 + { 1 \over t} \right)^{t+1} \right)^{-1}
この$t$ を $t\rightarrow \infty$ とすると、ネイピア数の定義から
\lim_{n \rightarrow \infty} \left( \left( 1 + { 1 \over t} \right)^{t+1} \right)^{-1} = e^{-1}
となり、ブートストラップサンプルの選ばれなかった部分であるOOBの比率はなんとネイピア数の逆数でした!
計算してみると、確かに約36%になっています!
np.e**-1
0.36787944117144233
参考
本記事のPythonコード(GitHub)
https://github.com/matsuken92/Qiita_Contents/blob/master/General/OOB-test.ipynb
Scikit-Learn OOB Errors for Random Forests
http://scikit-learn.org/stable/auto_examples/ensemble/plot_ensemble_oob.html