分位点回帰、という手法のご紹介です。
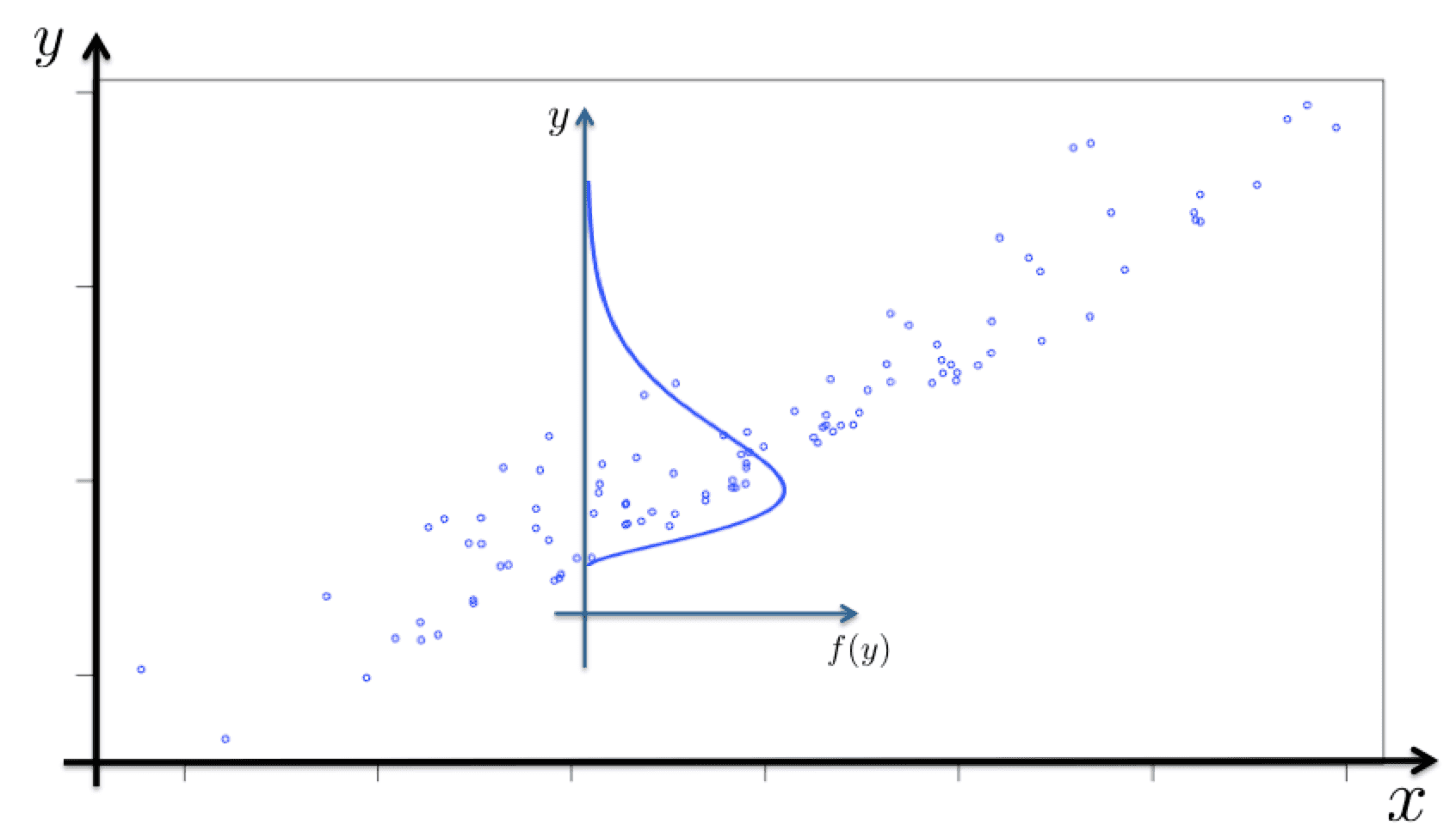
通常の回帰直線は、$x$が与えられた時の$y$の条件付き期待値(平均)と解釈できますが、分位点回帰では、25%分位点、とか95%分位点、等で使われる "分位点" をベースに回帰直線を引いてみようというものです。
何はともあれ、まずはこれを使ってグラフを書いて可視化を試みます。
1.誤差の分散が説明変数に依存した正規分布の例#
説明変数$x$が小さいところでは誤差の分散が小さく、大きいところでは誤差の分散も大きくなるようなケースです。そんなデータを生成して試しています。
分位点回帰では、分位点ごとに異なる $\beta$が設定されるので、それぞれ傾きが異なります。
分位点回帰の実行結果
下から順に5%, 10%, 25%, 75%, 90%, 95%の分位点回帰直線と、通常の回帰直線です。
まずはデータを生成して散布図を描きます。
# 未インストールならインストールする。
# install.packages('quantreg')
library(quantreg)
b <- -5 # 直線の傾き
a <- 35 # 直線の切片
data_x <- runif(500, 0, 5) # 0-5の間の一様乱数
data_y <- rep(0, length(data_x))
for (i in 1:length(data_x)){
# 切片:a, 傾き:b の直線に誤差がのるモデル
data_y[i] <- b*data_x[i] + a + rnorm(1, mean=0, sd=1+ data_x[i]) # 説明変数の大きさに依存した分散を設定
}
# 散布図を描画
plot(data_x, data_y, xlab="Random Variable", ylab="Random Variable",
type = "n", cex=.5, xlim=c(0, 5), ylim=c(0, 40))
points(data_x, data_y, cex=.5, col="blue")
この生成したデータに対して、分位点回帰を5%, 10%, 25%, 75%, 90%, 95%で各々実施し、直線を描画。合わせて通常の直線回帰をした結果も描画して比較します。
この例では、誤差の分布に正規分布を用いており、左右対称であるため、中央値の分位点回帰直線と、平均値を表す通常の直線回帰の結果がほとんど同じになります。
taus <- c(.05, ,.95, .10, .90, .25, .75) # 分位点を設定
cols <- c(4, 3, 2, 2, 3, 4) # 直線の色を塗り分け
xx <- seq(min(data_x), max(data_x), .1)
f <- coef(rq( (data_y) ~ (data_x), tau=taus) ) # 分位点回帰の計算実行
yy <- cbind(1,xx) %*% f
# 分位点回帰直線の描画
for(i in 1:length(taus)){
lines(xx, yy[,i], col=cols[i]))
}
abline(lm(data_y ~ data_x), col="red", lty = 2, lw=2) # 通常の回帰直線を描画
abline(rq(data_y ~ data_x), col="black", lw=2) # 中央値(median)の分位点回帰直線を描画
legend(0, 8, c("mean (LSE) fit", "median (LAE) fit"), col = c("red","black"),lty = c(2, 1), lw=c(1, 2))
2.誤差が指数分布している例#
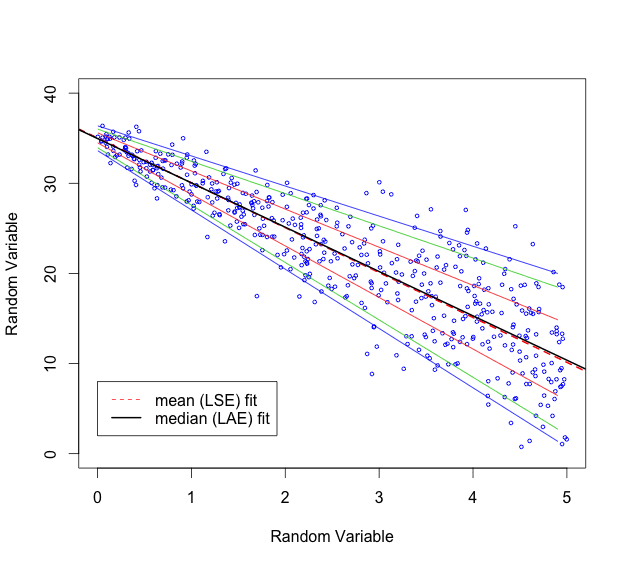
左右対称の分布の場合、面白みが少ないので、右に裾の長い指数分布を使ってデータを生成してみて、分位点回帰を当てはめてみます。
すると、赤い点線で表されている最小二乗法の直線よりも、黒い直線であわらされている中央値の分位点回帰の方がもっともらしい位置に直線が引かれています。裾が長い分布を使っているので、下側の分移転は密集していて、上側の分位点は距離が開いていることが特徴的です。
誤差が指数分布するデータを生成して散布図を描画します。
# 未インストールならインストールする。
# install.packages('quantreg')
library(quantreg)
# b : 直線の傾き
# lambda : 指数分布のパラメーター
# taus : 分位点を定義するリスト ex: c(.05, .95, .10, .90, .25,.75)
quant_reg_exp <- function(b, lambda, taus){
Dat <- NULL
Dat$x <- rnorm(100, mean=50, sd=7) # 説明変数は平均:50, 標準偏差:7の正規分布で生成
Dat$y <- rep(0, 100)
for (i in 1:length(Dat$x)){
Dat$y[i] <- b * Dat$x[i] + rexp(1, lambda) # 指数分布に従う誤差を生成
}
data_x = Dat$x
data_y = Dat$y
# 散布図を描画
plot(data_x, data_y ,xlab="Random Variable", ylab="Random Variable", type="n", cex=.5)
points(data_x, data_y ,cex=.5, col="blue")
xx <- seq(min(data_x), max(data_x), .1)
f <- coef(rq((data_y)~(data_x), tau=taus)) # 分位点回帰の計算実行
yy <- cbind(1,xx)%*%f
# 直線を描画
cols <- c(2, 2, 3, 3, 4, 4)
for(i in 1:length(taus)){
lines(xx, yy[,i], col=cols[i])
}
abline(lm(data_y ~ data_x), col="red", lty=2) # 通常の回帰直線を描画
abline(rq(data_y ~ data_x), col="black", lw=2) # 中央値(median)の分位点回帰直線を描画
legend(min(data_x), max(data_y), c("mean (LSE) fit", "median (LAE) fit"),
col=c("red","black"), lty=c(2,1), lw=c(1,2))
}
# param: b, lambda, taus
quant_reg_exp(.5, .5, c(.05, .95, .10, .90, .25,.75))
3.理論的なことをさわりだけ#
ほんのさわりだけですが、最小二乗法との違いのポイントについて記載してみようと思います。詳細は下記に記した参考文献をごらんください。
下記の青い線が $1/2 x^2$ の関数を描画したもので最小二乗法で使われる誤差を評価する関数を表します。
赤い線が$\tau$に応じた非対称の絶対値関数を描画したもので、分位点回帰の誤差を評価する関数として利用されるものです。分位点$\tau$に応じて誤差評価関数が変化します。
どちらも、0を起点として、その0からの距離をなんらか評価するための関数となっています。主に、マイナス方面の距離をプラスに変える、ということがポイントですね。分位点回帰はこれを左右非対称にすることにより、真ん中を当てに行くのではなく、指定された分位点 $\tau$を表そうとしています。
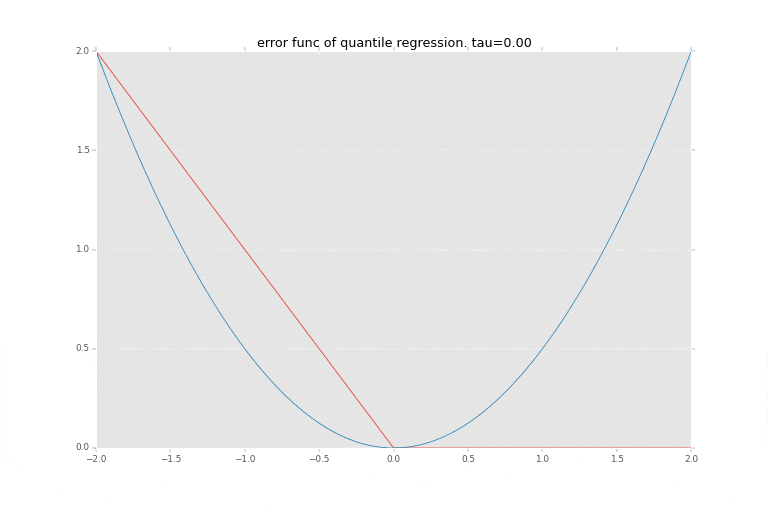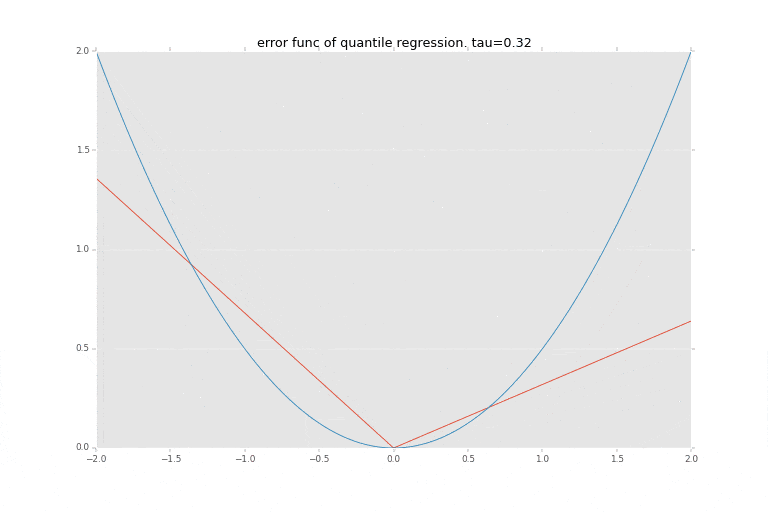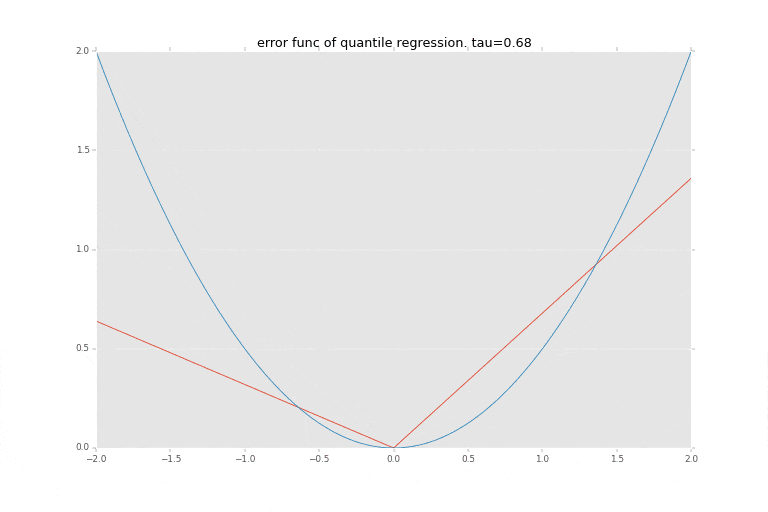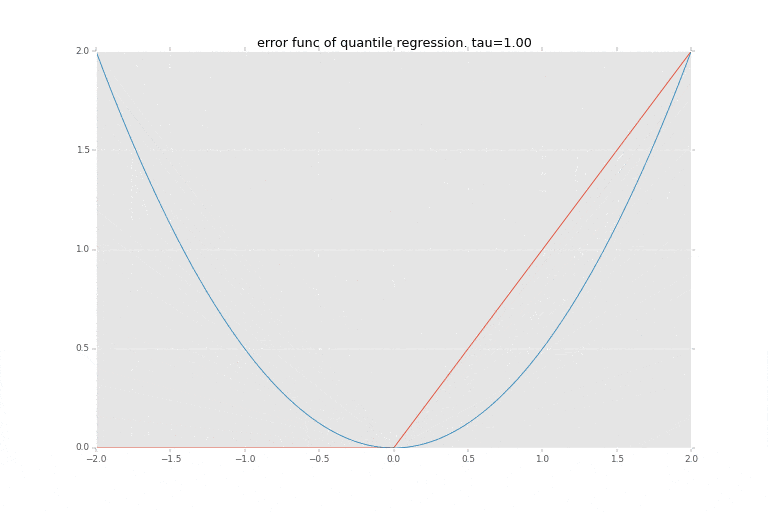
(描画コードはこちら。これはPythonで書いてます・・・)
分位点 $\tau$における分位点回帰直線 $\hat{g_{\tau}}$は下記のように定義することができます。関数 $\psi_{\tau}(\cdot)$ で評価した誤差を最小にする$g(\cdot)$を探す問題ですね。
\hat{g_{\tau}} = \arg\min_{g \in \mathcal{G}} \sum_{i=1}^{n} \psi_{\tau} \{ y_i - g(x_i) \}
この時、最小二乗法のときは関数 $\psi(\cdot)$(青い線の方)は
\psi_{\tau}(r) = {1 \over 2} r^2
を使いますが、分位点回帰では下記の非対称絶対値関数(赤い線の方)を使用して誤差を評価します。
\psi_{\tau}(r) =
\begin{cases}
(\tau − 1)\ r & {\rm if}\ \ r \le 0\\
\tau r & {\rm if}\ \ 0 < r
\end{cases}
ここで、$g(\cdot)$に線形な関数を仮定すると、
g(x_i) = \alpha + \beta x_i
となり、上の式の誤差関数の値を最小にするような$\alpha, \beta$を求める、という問題になります。
$y$の推定量を $\hat{y} = g(x_i)$ とします。
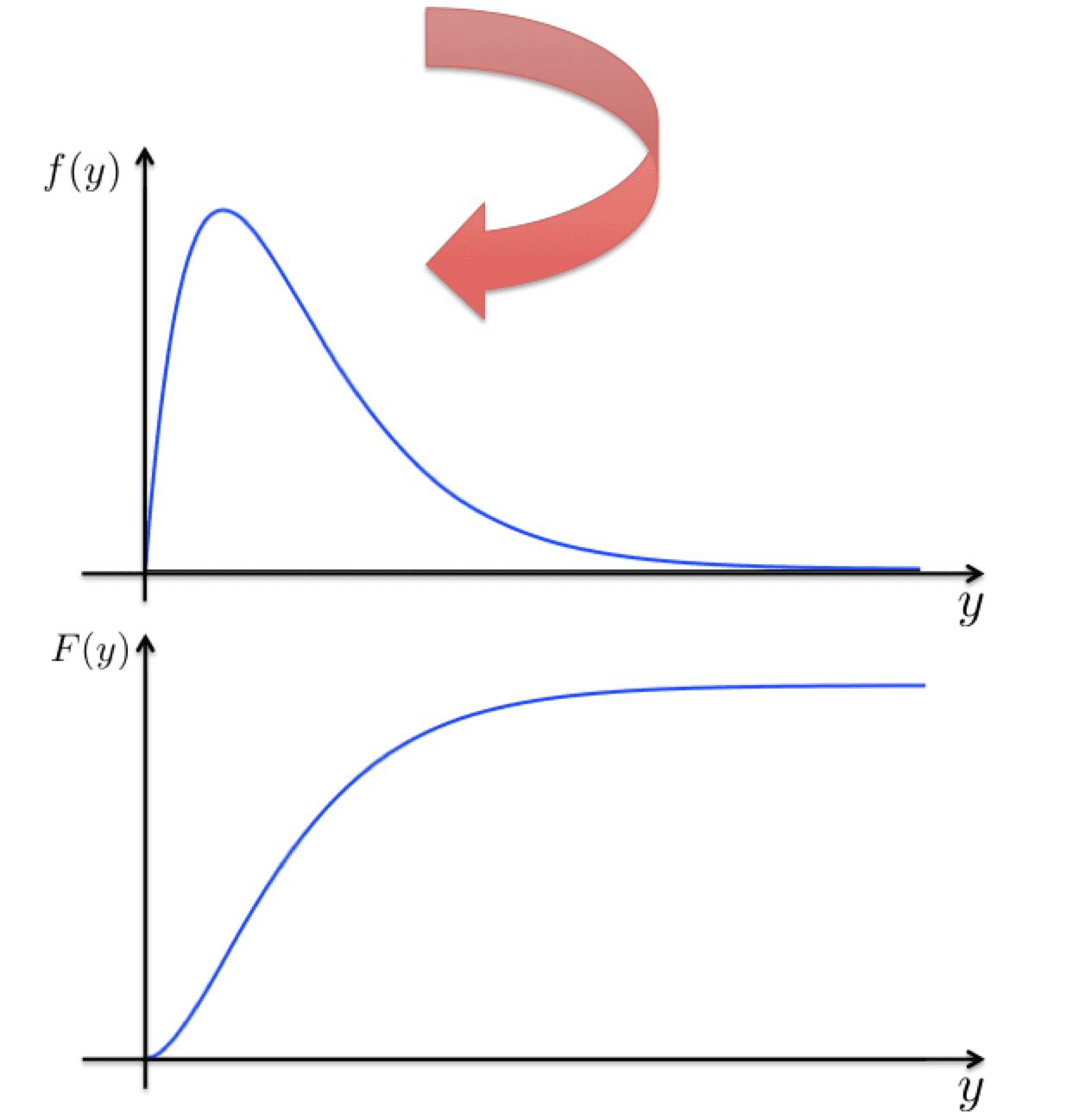
また、誤差の密度関数、累積密度関数を $f(y),\ F(y)$ とします。
図示すると下記のイメージです。
誤差関数$L()$を下記で定義します。
L(\hat{y}) = E[\psi_{\tau} \{ y_i - \hat{y} \} ]
= (\tau -1) \int_{-\infty}^{\hat{y}} (y-\hat{y})\ f(y) \ dy
+ \tau \int^{\infty}_{\hat{y}} (y-\hat{y})\ f(y)\ dy
誤差関数 $L(\cdot)$を $\hat{y}$で微分して0とおくと、
{\partial L \over \partial \hat{y}} =
(\tau -1) \int_{-\infty}^{\hat{y}} (-1)\ f(y) \ dy
+ \tau \int^{\infty}_{\hat{y}} (-1)\ f(y) \ dy \\
= \int_{-\infty}^{\hat{y}}\ f(y) \ dy - \tau\ \left( \int_{-\infty}^{\hat{y}}\ f(y) \ dy + \int^{\infty}_{\hat{y}}\ f(y) \ dy \right) \\
= F(\hat{y}) - \tau = 0
よって、
F(\hat{y}) = \tau
が成り立ち、$\tau$が $\hat{y}$における分位点 $F(\hat{y})$に等しくなります。
4.参考文献等#
[1] ‘quantreg’ manual
https://cran.r-project.org/web/packages/quantreg/quantreg.pdf
[2] Wikipedia "Quantile Regression"
https://en.wikipedia.org/wiki/Quantile_regression
[3] 適応的分位点回帰分析に関する研究[森口浩行]
http://miuse.mie-u.ac.jp/bitstream/10076/10813/1/M2008288.pdf
[4] 京都大学 平成25年度 ミクロ計量経済学 講義ノート8 分位点回帰 [奥井亮]
http://www.okui.kier.kyoto-u.ac.jp/doc/quantile.pdf
[5] 分位点回帰による効率賃金仮説の検証[中村和敏]
http://reposit.sun.ac.jp/dspace/bitstream/10561/746/1/v43n4p87_nakamura.pdf