データ解析はまだまだブームのようです。機械学習であれ何であれ、まずデータが与えられてすることは、データを視覚化して、解析のとっかかりとなる仮説をつかむことですね。仮説を検証するため、様々な解析をして様々な統計量を計算します。
そんなことをしていると、ある統計量の母集団におけるバラツキが知りたい、という事態に出くわすことがあります。
それがデータの平均値であれば、標準誤差 (standard error of the mean)というものを計算すればOKです。標準偏差を、データ数の平方根で割ったものですね。
ところが、解析では平均だけでなく、中央値 (median)、百分率 (centile)、相関係数 (correlation coefficient)など様々な統計量を見ていくことになります。そして、これらには標準誤差や信頼区間 (confidence interval)といったバラツキを定量化できる簡単な公式が存在しません。
そんなときに役に立つのが、再標本化 (resampling)、特に、ブートストラップ (Bootstrap) という手法です。
ブートストラップとは
ブートストラップではまず、再標本化 (resampling)によって元データから何千もの似たデータセットを作り出します。そして、それぞれのデータセットで、欲しい統計量を計算します。すると、その統計量の分布ができるので、その分布の標準偏差を計算することにより、その統計量の標準誤差を求めることができます。
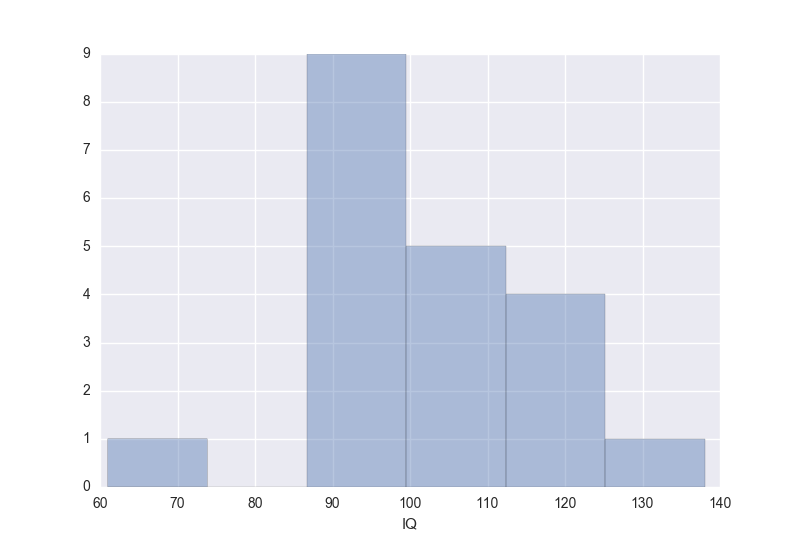
例として、20人のIQのデータがあったとします。値はそれぞれ、61, 88, 89, 89, 90, 92, 93, 94, 98, 98, 101, 102, 105, 108, 109, 113, 114, 115, 120, 138だとしましょう。分布は以下のような感じです。
このとき、平均値 (mean) は100.85、平均値の標準誤差 (standard error of the mean) は3.45になります。
ただ、こうした値の分布って、所得とかもそうですけど、平均値 (mean) よりも中央値 (median) の方が人の実感を反映してるんですよね。なので、今回はブートストラップを使って、中央値のバラツキ、すなわち中央値の標準誤差 (standard error of the median) を求めてみたいと思います。
ブートストラップのアルゴリズム
ブートストラップは、以下の流れで行います。
1: 何回再標本化するか決めます。
500, 1000, 10000, 100000など、キリが良く、大きい数にしましょう。今回は1000でやってみます。
2: 再標本化して、人工的にデータを生成します。このとき、重複を許して元データの標本数だけ、データ標本を取り出します。
例えば、元データが$X_1,X_2,...,X_5$と$5$個あったとしたら、再標本化するたびに生成されるデータセットの例は以下のようになります。
再標本1 = $X1,X2,X3,X3,X4$
再標本2 = $X1,X1,X3,X4,X4$
再標本3 = $X2,X2,X5,X5,X5$
......
再標本998 = $X1,X2,X3,X4,X5$
再標本999 = $X1,X3,X4,X5,X5$
再標本1000 = $X3,X3,X3,X3,X4$
こうして、ステップ1で決めた数だけ、重複を許しデータ標本を元データ数だけ取り出すことを繰り返し、人工的にデータを作ってしまいます。
各再標本にどのデータ標本が入るかはランダムです。5個すべて同じ値が入るときもあるかもしれませんし、5個全て違う値が入るときもあるでしょう。
3: 各再標本で、求めたい統計量を計算する。
中央値なりなんなり、それぞれの再標本データを使って統計量を求めます。1000回再標本化したら、統計量も1000個とれますね。
再標本1 = $X1,X2,X3,X3,X4$ $\to$ 統計量 = $S1$
再標本2 = $X1,X1,X3,X4,X4$ $\to$ 統計量 = $S2$
再標本3 = $X2,X2,X5,X5,X5$ $\to$ 統計量 = $S3$
......
再標本998 = $X1,X2,X3,X4,X5$ $\to$ 統計量 = $S998$
再標本999 = $X1,X3,X4,X5,X5$ $\to$ 統計量 = $S999$
再標本1000 = $X3,X3,X3,X3,X4$ $\to$ 統計量 = $S1000$
たくさん統計量がとれましたね。そして、こう考えます。
「このたくさんの統計量の分布って、その統計量の母集団分布とほぼ同じと考えていいよね!だってどうせもっと実験してデータをたくさん取ったところで、似たような値のデータが増えるだけだからね!!」
つまりブートストラップでは、実験的にではなく、統計のトリックを使ってデータ数を増やしているのですね。そしてデータ数がある程度大きければ、その分布は限りなく母集団の分布に近いはずだ、という想定をしています。
4: 求めた統計量の分布を使って、バラツキ(標準誤差、信頼区間など)を計算する。
例えば標準誤差は、母集団分布の標準偏差のことなので、単純に、求められた統計量分布の標準偏差を求めればいいですね。
こうして、めでたく気になる統計量のバラツキを求めることができます。
ブートストラップの実践
pythonでやってみましょう (Matlab/Octaveも下にあります)。
まず、必要なライブラリをゲットします。
# import librarys
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Numpyを使って、データをアレイに入れます。
# get data
iq = np.array([61, 88, 89, 89, 90, 92, 93,
94, 98, 98, 101, 102, 105, 108,
109, 113, 114, 115, 120, 138])
基本統計量として、平均値、平均値の標準誤差、中央値を計算します。
# compute mean, SEM (standard error of the mean) and median
mean_iq = np.average(iq)
sem_iq = np.std(iq)/np.sqrt(len(iq))
median_iq = np.median(iq)
それぞれ、平均値: 100.85、平均値の標準誤差: 3.45、中央値: 99.5 と計算できました。
中央値の標準誤差を求めるため、ブートストラップを実行します。ブートストラップが正しくできてるかの sanity check として、一応平均値の標準誤差も一緒に計算しています。
pythonで、1~nの連続した整数値を重複ありでランダムに並び替えるには、以下のようにします。
np.random.choice(n,n,replace=True)
これを使って、bootstrapの再標本化を行います。
# bootstrap to compute sem of the median
def bootstrap(x,repeats):
# placeholder (column1: mean, column2: median)
vec = np.zeros((2,repeats))
for i in np.arange(repeats):
# resample data with replacement
re = np.random.choice(len(x),len(x),replace=True)
re_x = x[re]
# compute mean and median of the "new" dataset
vec[0,i] = np.mean(re_x)
vec[1,i] = np.median(re_x)
# histogram of median from resampled datasets
sns.distplot(vec[1,:], kde=False)
# compute bootstrapped standard error of the mean,
# and standard error of the median
b_mean_sem = np.std(vec[0,:])
b_median_sem = np.std(vec[1,:])
return b_mean_sem, b_median_sem
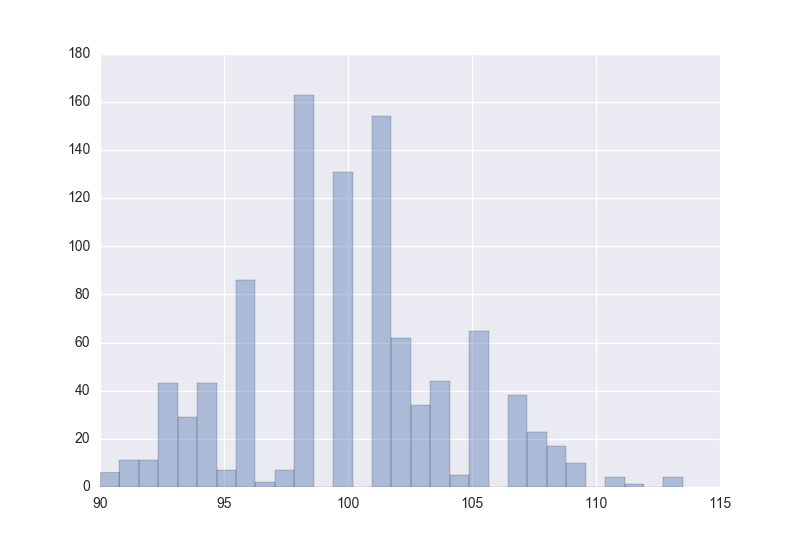
この関数を x = iq, repeats = 1000 として実行すると、ブートストラップによって求められた1000個の中央値の分布をみることができます。
……もっと繰り返しを増やした方がよかったかもですね。
とりあえず、この分布から中央値の標準誤差を求めることができます。単に1000個の中央値の標準偏差を計算するだけです。
- ブートストラップで求められた中央値の標準誤差: 4.22
同じように、平均値の標準誤差も計算します。
- ブートストラップで求められた平均値の標準誤差: 3.42
最初に、元データから求めた平均値の標準誤差は3.45なので、結構近いですね。ブートストラップは正しく統計量のバラツキを推定したようです。
注意点
ブートストラップではランダムに再標本化するため、実行するたびに結果が少しずつ異なります。結果のバラツキを減らし、より正確な推定をするには、繰り返し数を増やす (~10,000) 必要があります。
まとめのまとめ
ブートストラップでは再標本化により、興味のある統計量のバラツキを推定することができる。
終わりに
ブートストラップをはじめ、統計学の中でも再標本化 (resampling) を考えた人は天才だと思います。データを人工的に増やして母集団分布を近似してしまうなんて、とりあえずデータをひたすら集め続ける苦行から解放されるわけですね!もちろん、ある程度データを実際にとって母集団の代表例を集めなければ、いくら再標本化しても永遠に母集団には近づけませんが……。
ソースコードは以下に載せておきます。
# import librarys
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# get data
iq = np.array([61, 88, 89, 89, 90, 92, 93,
94, 98, 98, 101, 102, 105, 108,
109, 113, 114, 115, 120, 138])
# compute mean, SEM (standard error of the mean) and median
mean_iq = np.average(iq)
sem_iq = np.std(iq)/np.sqrt(len(iq))
median_iq = np.median(iq)
# bootstrap to compute sem of the median
def bootstrap(x,repeats):
# placeholder (column1: mean, column2: median)
vec = np.zeros((2,repeats))
for i in np.arange(repeats):
# resample data with replacement
re = np.random.choice(len(x),len(x),replace=True)
re_x = x[re]
# compute mean and median of the "new" dataset
vec[0,i] = np.mean(re_x)
vec[1,i] = np.median(re_x)
# histogram of median from resampled datasets
sns.distplot(vec[1,:], kde=False)
# compute bootstrapped standard error of the mean,
# and standard error of the median
b_mean_sem = np.std(vec[0,:])
b_median_sem = np.std(vec[1,:])
return b_mean_sem, b_median_sem
# execute bootstrap
bootstrapped_sem = bootstrap(iq,1000)
Matlab/Ovctaveは以下です。
function bootstrap_demo
% data
iq = [61, 88, 89, 89, 90, 92, 93,94, 98, 98, 101, 102, 105, 108,109, 113, 114, 115, 120, 138];
% compute mean, SEM (standard error of the mean) and median
mean_iq = mean(iq);
sem_iq = std(iq)/sqrt(length(iq));
median_iq = median(iq);
disp(['the mean: ' num2str(mean_iq)])
disp(['the SE of the mean: ' num2str(sem_iq)])
disp(['the median: ' num2str(median_iq)])
disp('---------------------------------')
[b_mean_sem, b_median_sem] = bootstrap(iq, 1000);
disp(['bootstrapped SE of the mean: ' num2str(b_mean_sem)])
disp(['bootstrapped SE of the median: ' num2str(b_median_sem)])
% bootstrap to compute sem of the median
function [b_mean_sem, b_median_sem] = bootstrap(x, repeats)
% placeholder (column1: mean, column2: median)
vec = zeros(2,repeats);
for i = 1:repeats
% resample data with replacement
re_x = x(datasample(1:length(x),length(x),'Replace',True));
% compute mean and median of the "new" dataset
vec(1,i) = mean(re_x);
vec(2,i) = median(re_x);
end
% histogram of median from resampled dataset
histogram(vec(2,:))
% compute bootstrapped standard error of the mean, and standard error of
% the median
b_mean_sem = std(vec(1,:));
b_median_sem = std(vec(2,:));