はじめに
非可換な演算子$X, Y$について、以下のLie-Trotter公式が成り立つ。
\exp(h(X+Y)) = \left( \exp(hX/n)\exp(hY/n) \right)^n + O\left(\frac{h^2}{n}\right)
ここで$n$は分解数(トロッター数)である。この公式は$h$に関するテイラー展開としては$h$の一次までしか正しくなく、それを反映して打切り誤差は$O(h^2/n)$となる。ここで、展開の形を工夫すると次数を上げることができる。
\exp(h(X+Y)) = \left( \exp(hX/2n)\exp(hY/n)\exp(hX/2n) \right)^n + O\left(\frac{h^3}{n^2}\right)
これは二次の対称分解と呼ばれ、テイラー展開が$h^2$の次数まで正しい。それを反映して打切り誤差が$O(h^3/n^2)$となる。
本稿は、この近似精度の向上を確認する。
ソースは
https://github.com/kaityo256/lie-trotter-sample
においてある。
ソースの解説
やってることは前の記事と同じなのでそちらを参照。一次の分解の場合は
def trotter(X,Y,Z,h,n):
eZ = calc_exp(Z,h)
eX = calc_exp(X,h/n)
eY = calc_exp(Y,h/n)
S = np.diag(np.ones(d))
eXeY = eX.dot(eY)
for i in range(n):
S = S.dot(eXeY)
return linalg.norm(eZ - S)/linalg.norm(eZ)
と書いていたのを、二次の対称分解の場合は
def trotter2nd(X,Y,Z,h,n):
eZ = calc_exp(Z,h)
eX = calc_exp(X,h/n*0.5)
eY = calc_exp(Y,h/n)
S = np.diag(np.ones(d))
eXeYeX = eX.dot(eY.dot(eX))
for i in range(n):
S = S.dot(eXeYeX)
return linalg.norm(eZ - S)/linalg.norm(eZ)
と書くだけ。難しいことは無いと思う。
結果
二次の対称分解を行った結果は以下の通り。
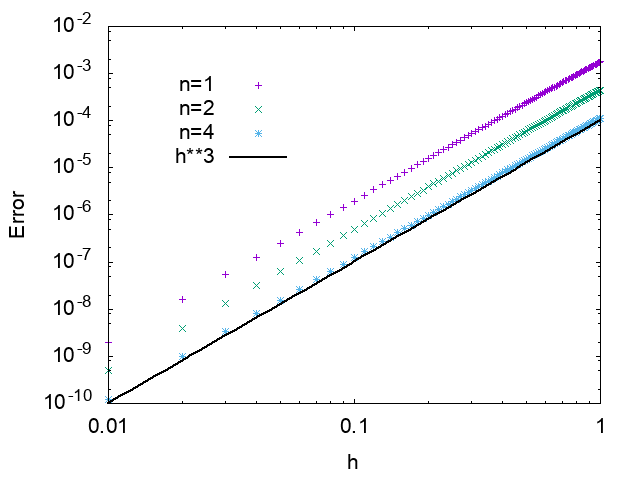
まず、打切り誤差の時間刻み$h$依存性。$n$を1,2,4とし、それぞれについていろんな$h$の値で打切り誤差を評価する。
分解数$n$に依らずに$O(h^3)$と、精度が向上していることがわかる。
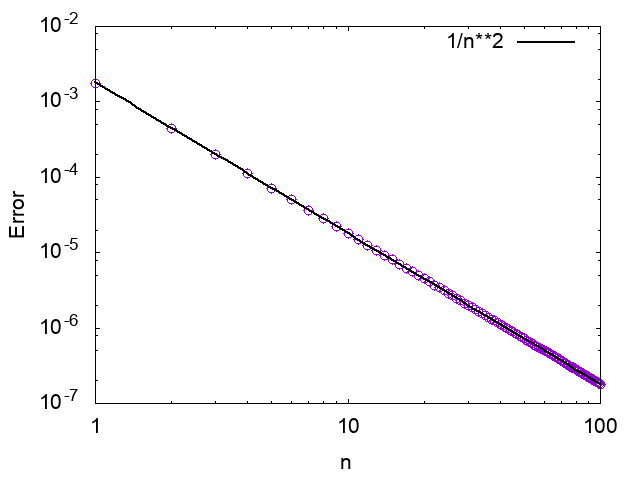
次は分解数$n$の依存性。時間刻み$h$は$1.0$固定。
誤差が$O(1/n^2)$と、こちらも精度が向上していることがわかる。
まとめ
トロッター分解において、二次の対称分解を用いると精度が向上することを確認した。ここで、
\begin{align}
U_X(h) &= \equiv \exp(h X) \\
U_Y(h) &= \equiv \exp(h Y)
\end{align}
と書くと、$n=3$の場合の一次の分解は
\exp(h(X+Y)) \sim U_X(h/3)U_Y(h/3)U_X(h/3)U_Y(h/3)U_X(h/3)U_Y(h/3)
と書ける。$U_X(h_1)U_X(h_2) = U_X(h_1 + h_2)$が成り立つことから、二次の対称分解は
\exp(h(X+Y)) \sim U_X(h/6)U_Y(h/3)U_X(h/3)U_Y(h/3)U_X(h/3)U_Y(h/3) U_X(h/6)
と、一次の分解に比べて左端の演算子を半分だけ右端に移動させた形になっている。$n$が増えても、両者の違いはこの端っこだけ。たったこれだけのことで演算子の近似精度が$h$、$n$ともに一次上がるって不思議じゃないですか?1
-
職場の人には「当たり前というか、よくあることじゃないですか」って言われたけど・・ ↩