藤井四段の連勝が止まらないですね。
21日の対局に勝利して、連勝記録を1位タイの28連勝まで伸ばしてきました。26日の対局で勝利すれば単独トップになります。
そんな藤井四段の対戦成績は28勝0負。勝率でいうと1.000です。クラクラするような成績ですが、この「勝率」とは何かを少し数学的にみてみましょう。
単純に言葉だけをみると「藤井四段が勝利する確率」ではないかと考えられます。つまり
$$P(\text{勝利}\ |\ \text{藤井四段}) = 1.0$$かのように感じます。
ではここで、26日の対局で藤井四段が勝利する確率はどれだけでしょう?
$P(\text{勝利}\ |\ \text{藤井四段}) = 1.0$として考えると、これはつまり藤井四段は必ず勝つので、100%になってしまいます。しかし、もちろんそんなことはありません。藤井四段ですらも負けることはあるはずです。
実はここで計算されている1.0という値は最尤推定という方法で推定された藤井四段が勝利する確率になっています。つまり、実際の値ではなく、「こんな感じなんじゃないかな?」と推測された値になっているのです。
最尤推定
ここから、最尤推定とは何かの話をしていきます。
さて、藤井四段が勝利する確率を$\theta$と書くことにしましょう。
もし、実は藤井四段は別にすごいプロ棋士ではなく$\theta=0.5$であったとしましょう。そんな藤井四段がたまたま28連勝する確率はどれだけになるでしょう?これは、確率0.5で起こる事象が28回起こる確率なので
$$p(\text{28連勝}\ |\ \theta=0.5) = 0.5^{28} = 0.0000000037$$となります。
こんなことはおこりそうもないですが、一応可能性としてはありえます。
次に、$\theta=0.9$だとしましょう。すると、
$$p(\text{28連勝}\ |\ \theta=0.9) = 0.9^{28} = 0.052$$となります。
だいたい5%ぐらいなので、これはありうるかもしれませんね。
ここまで考えるとまず、28連勝したという事実から実際に藤井四段が勝つ確率$\theta$は導くことができないということがわかります。もしかすると、本当は$\theta=0.5$でたまたますごく運がよかったのかもしれないし、$\theta=0.9$で5%の確率が起きたのかもしれません。
そこで、実際の$\theta$の値を求めることは諦めて、こうなんじゃないかな?と推定することにします。このとき、実際に起きたこと(28連勝)が一番起きやすいような$\theta$で推定するというのが最尤推定です。
この実際に起きたことをデータ$D$とすると、
$$\text{argmax}_{\theta} P(D|\theta)$$と書けます。
最尤推定とは尤度を最大にするように推定するという意味です。尤度とはデータが起こる確率$P(D)$のことを言います。これを最大にするようなパラメータ$\theta$を推定するということになります。
では実際に最尤推定を使って藤井四段の勝つ確率$\theta$を推定してみましょう。
$$P(\text{28連勝}\ |\ \theta) = \theta^{28}$$なので、これを最大にするような$\theta$は$\theta=1.0$になりますね。
これが藤井四段の勝率なのです。
藤井四段は少し特殊すぎる例なので、もう少し一般化して考えてみましょう。
$N$回対局して$n$回勝利した棋士がいたとします。この棋士の勝利確率を最尤推定してみましょう。
勝利確率を$\theta$として、$N$対局中$n$回勝利する確率を考えると
P(n|N, \theta) = \binom{N}{n}\theta^n(1-\theta)^{N-n}
となります。これを最大化するような$\theta$を探すので、まず微分を取り
\begin{align*}
\frac{dP}{d\theta}
&= \binom{N}{n}\left(n\theta^{n-1}(1-\theta)^{N-n}-(N-n)\theta^n(1-\theta)^{N-n-1}\right)\\
&= \binom{N}{n}\theta^{n-1}(1-\theta)^{N-n-1}\left(n(1-\theta)-(N-n)\theta\right)\\
&= 0
\end{align*}
とします。
$\binom{N}{n}$や$\theta^{n-1}(1-\theta)^{N-n-1}$は0にならないので、
n(1-\theta)-(N-n)\theta=0
となり、とけば
\theta=\frac{n}{N}
が得られます。
これは、いわゆる勝率になっていますね。
MAP推定(最大事後確率推定)
最尤推定の問題点はデータの数が少ないときです。例えば、3回しか対局をしていない棋士の勝率はあまり信用できません。本当はすごく強いのにたまたま3回の対局で調子が出なかった。ということがあるかもしれないし、その逆もあり得ます。
そこで考えられたのがMAP推定です。日本語では最大事後確率推定という仰々しい名前がついています。
MAP推定に入る前にベイズの定理を知らなければいいけません。
ベイズの定理
二つの事象$A, B$の同時確率を考えると、これは$A$が起きてその中で$B$も起きる確率なので
P(A, B) = P(B\ |\ A)P(A)
となります。
これは$A, B$を入れ替えても成り立つので
P(A, B) = P(A\ |\ B)P(B)
も成り立ちます。
これをつなぎ合わせると
P(A\ |\ B)P(B) = P(B\ |\ A)P(A)
がわかります。ここから
P(A\ |\ B) = \frac{P(B\ |\ A)P(A)}{P(B)}
となります。これが機械学習の手法などでとてもよく使われるベイズの定理です。
もう少し詳しくみていくと、これは$P(A\ |\ B)$と$P(B\ |\ A)$を入れ替える定理と考えることができます。
ここで、$A$を求めたい数値$\theta$として$B$をデータ$D$としましょう。するとこれは
P(\theta\ |\ D) = \frac{P(D\ |\ \theta)P(\theta)}{P(D)}
となります。ここで、$P(\theta)$をデータが手に入る前の確率分布なので事前分布。逆に$P(\theta\ |\ D)$をデータが手に入った後の確率分布なので事後分布と言います。
この事後分布が最大になるような$\theta$を選ぼうというのがMAP推定です。数式で書けば
\text{argmax}_\theta P(\theta\ |\ D) = \text{argmax}_\theta \frac{P(D\ |\ \theta)P(\theta)}{P(D)}
となりますが、分母の$P(D)$は$\theta$に関係ないので無視してよく、
\text{argmax}_\theta P(D\ |\ \theta)P(\theta)
がMAP推定です。$N$対局中$n$回勝った将棋棋士について考えれば、
P(n\ |\ N, \theta) = \binom{N}{n} \theta^n(1-\theta)^{N-n}
です。では事前分布$P(\theta)$はなんでしょうか?実はこれは数学的に導くものではなく、人間が最初に設定してあげるものです。しかし、計算を簡単にするために共役事前分布という特別な性質を持ったものを使います。共役事前分布とは、事前分布と、事後分布が同じ形になるもののことです。
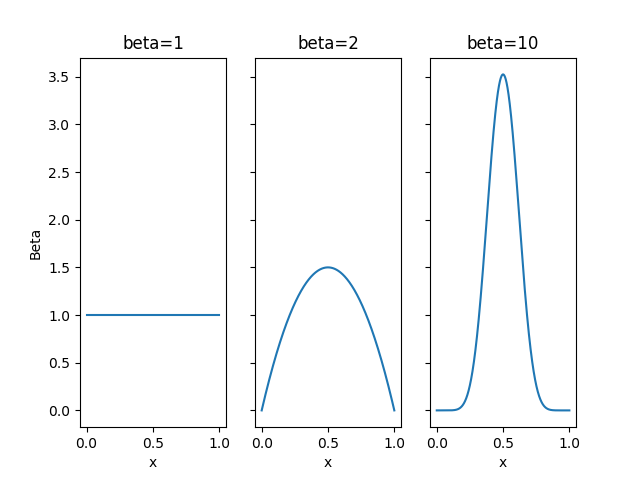
今回扱っている勝ち負けという結果が二つの場合はベータ分布という分布が共役事前分布になります。
ベータ分布は$\beta$をハイパーパラメータとしてとって、
P(\theta) = \text{Beta}(\theta\ |\ \beta) = \frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\theta^{\beta-1}(1-\theta)^{\beta-1}
となります。
前についている$\frac{\Gamma(2\beta)}{\Gamma(\beta)^2}$は積分した時の値を1にするためについているものです。
$\text{Beta}(\theta\ |\ \beta)$は平均値、最頻値は0.5になっています。
これを含めて、MAP推定をみてみると
\begin{align*}
\text{argmax}_\theta P(\theta\ |\ D)
&= \text{argmax}_\theta P(D\ |\ \theta)P(\theta)\\
&= \text{argmax}_\theta\binom{N}{n} \theta^n(1-\theta)^{N-n}\times\frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\theta^{\beta-1}(1-\theta)^{\beta-1}
\end{align*}
となります。$\theta$に関係ない部分を無視して
\text{argmax}_\theta P(\theta\ |\ D) = \text{argmax}_\theta \theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}
です。ここからは最尤推定と同じように$\theta$を計算すると、
\theta = \frac{n+\beta-1}{N+2(\beta-1)}
が得られます。
これを例えば$\beta=2$として藤井四段の勝利確率を推定してみると、
\frac{28+2-1}{28+2(2-1)} = \frac{29}{30} = 0.967
となります。この$\beta=2$としたものを特別にラプラススムージングと言います。
もっと大きな$\beta$で計算してみます。$\beta=10$とすれば、
\frac{28+10-1}{28+2(10-1)} = \frac{37}{46} = 0.80
このように$\beta$は大きくなればなるほど、より平均に近づけようとする力が働いて藤井四段の勝利確率の推定は小さくなっていきます。
ベイズ推定
さて、298対局して199勝した棋士と、4対局して3勝した棋士がいたとします。二人の勝利確率を$\beta=2$のMAP推定すると、ベテラン棋士は
\theta=\frac{199+2-1}{298+2(2-1)} = \frac{2}{3}
新人棋士は
\theta=\frac{3+2-1}{4+2(2-1)} = \frac{2}{3}
となり二人の勝利確率は同じになります。しかし、ベテラン棋士の値の方が信用できそうです。
しかし、この二つはMAP推定上では同じになってしまいます。これはargmaxをとったときに一番大きな値だけが考えられて、その値に対する信頼度は考慮されなくなってしまうからです。
「うーん、多分こっちなんじゃないかなー?」と「これは絶対こっちだね!」が区別されずに扱われてしまっているのです。
そこで、argmaxせずに$P(\theta\ |\ D)$をそのまま使おうというのがベイズ推定です。ベイズ推定では、$\theta$の値だけでなく、その値に対する自信も計算することができます。
早速ベイズ推定をやってみます。
ベイズの定理から
P(\theta\ |\ D) = \frac{P(D\ |\ \theta)P(\theta)}{P(D)}
です。 MAP推定ではargmaxをとったので、$P(D)$については無視してきましたが、ベイズ推定では考える必要があります。
\begin{align*}
P(D) &= \int^1_0P(D, \theta)d\theta\\
&= \int^1_0 P(D\ |\ \theta) P(\theta)d\theta\\
&= \int^1_0 \binom{N}{n} \theta^n(1-\theta)^{N-n} \frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\theta^{\beta-1}(1-\theta)^{\beta-1}d\theta\\
&= \binom{N}{n}\frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\int^1_0\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}d\theta
\end{align*}
これを使うと、
\begin{align*}
P(\theta\ |\ D) &= \frac{P(D\ |\ \theta)P(\theta)}{P(D)}\\
&= \frac{\binom{N}{n}\frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}}{\binom{N}{n}\frac{\Gamma(2\beta)}{\Gamma(\beta)^2}\int^1_0\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}d\theta}\\
&= \frac{\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}}{\int^1_0\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}d\theta}
\end{align*}
となります。
積分部分は
\int_0^1\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}d\theta
= \frac{\Gamma(n+\beta)\Gamma(N-n+\beta)}{\Gamma(N+2\beta)}
になります。これを使うと、
P(\theta\ |\ D) = \frac{\Gamma(N+2\beta)}{\Gamma(n+\beta)\Gamma(N-n+\beta)}\theta^{n+\beta-1}(1-\theta)^{N-n+\beta-1}
がわかります。
これが、ベイズ推定です。
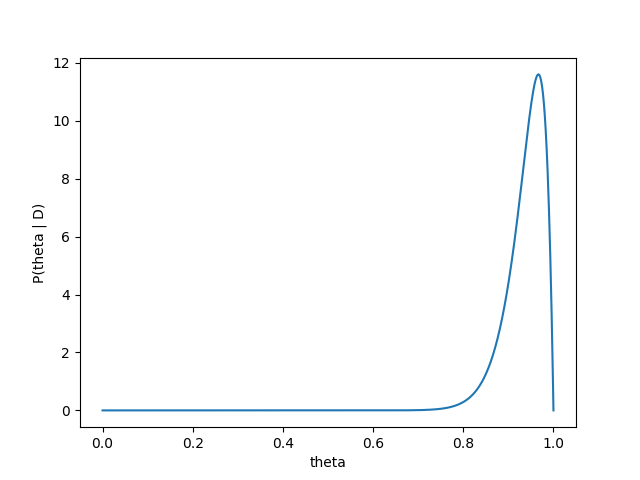
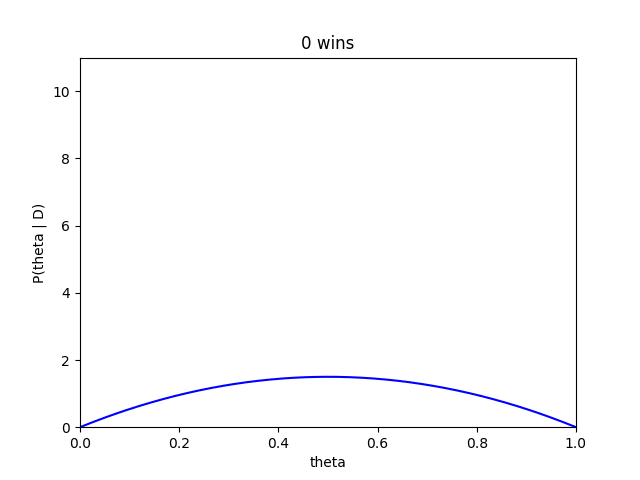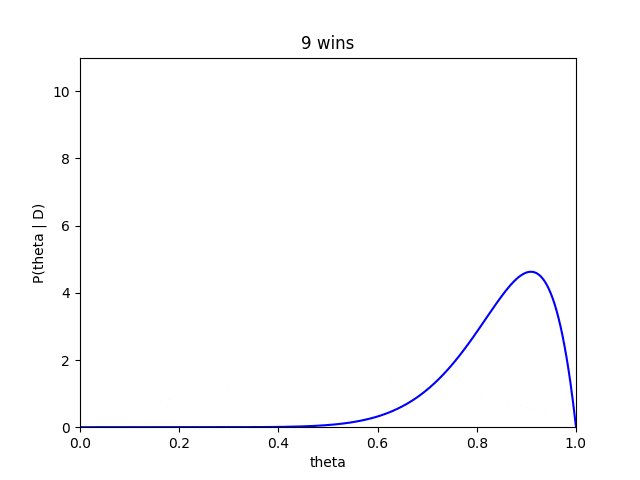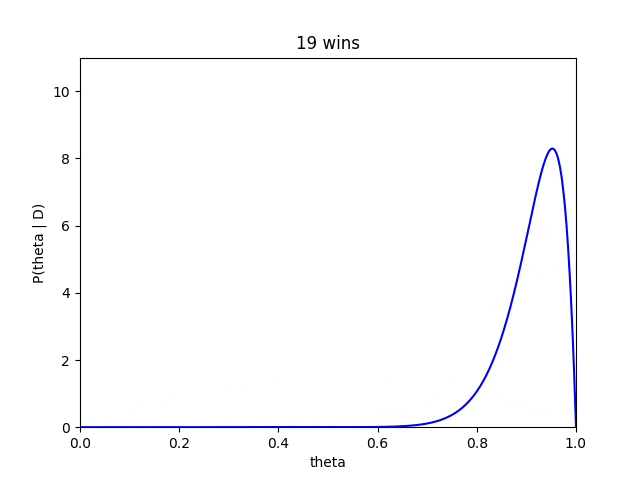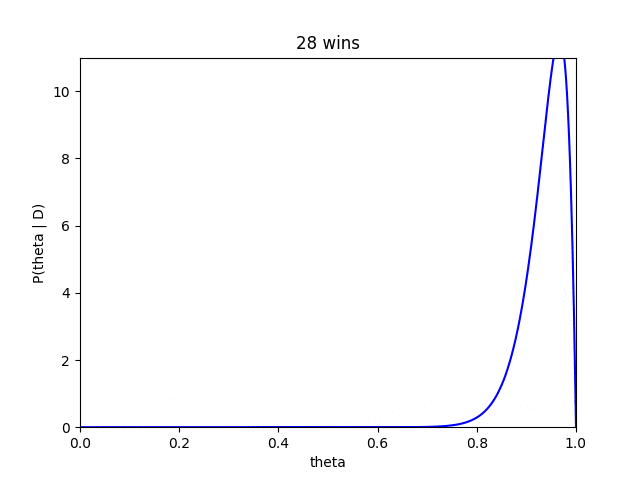
早速藤井四段の28連勝をベイズ推定してみます。藤井四段が28連勝したという情報をすでに受け取ったベイズ推定は
P(\theta\ |\ D) = \frac{\Gamma(28+2*2)}{\Gamma(28+2)\Gamma(0+2)}\theta^{28+2-1}(1-\theta)^{0+2-1}
= 930\theta^{29}(1-\theta)
となります。これをプロットすると、
となります。
相当高い値を考えていますね。
さらにベイズ推定では、藤井四段が勝つ毎にどのように推定が変化ていくかもみることができます。
藤井四段が勝ち星を重ねるたびにだんだんと、確信度が高くなり分布も高い方によっていく傾向がみて取れます。
ベイズ推定の問題点
ベイズ推定は、一つの値ではなくその確率分布になるので一つの値をだす最尤推
定やMAP推定に比べてより多くの情報が手に入ります。
じゃあみんな、ベイズ推定使えばいいじゃんというふうに思うかもしれませんが、ベイズ推定にも問題があります。
それは、積分$P(D) = \int_0^1 P(D | \theta)P(\theta)d\theta$を導く部分にあります。
今回は、シンプルな状況に対してベイズ推定を行ったのでこの値を明示的に導くことができました。しかし、多くの実践的な状況では、この値は単純には解けなく、別の方法を使って近似をしなければいけないことがあります。
ギブスサンプリングなどの手法がありますが、最尤推定やMAP推定などと比べて時間がかかったり、精度が出ないことがあります。このため、ベイズ推定ではうまくいかないことも多いのです。